[切换地区]
    当前位置：
  1. 资源平台
  2. 初中数学试卷
  3. {{getGradeName('2')}}

浙教版八年级数学上册基础训练：1.5 三角形全等的判定（四）

适用年级：{{getGradeNameByProperty('初二|同步测试|全国|2017年')}} 试卷类型：{{getTestPaperTypeName('初二|同步测试|全国|2017年')}} 使用省份：{{getAreaName('初二|同步测试|全国|2017年')}}
试卷年份：{{getYear('初二|同步测试|全国|2017年')}}上传日期：2017-10-27题数：12
浏览次数：262
提示：单击题文可显示答案与解析。
免费
题号：5065380 题型：选择题 难易度：较易 日期：2017-10-19 来源：浙教版八年级数学上册基础训练：1.5 三角形全等的判定（四）
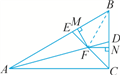
【题文】如图，已知∠ABC=∠BAD，添加下列条件还不能判定△ABC≌△BAD的是（    ）
A．AC=BDB．∠CAB=∠DBAC．∠C=∠DD．BC=AD

【答案】

【解析】

登录学易云，内容更精彩！ 抱歉，未登录用户无法看答案与解析！

立即登录 还不是学易云用户？

题号：5114182 题型：选择题 难易度：较易 日期：2017-10-27 来源：浙教版八年级数学上册基础训练：1.5 三角形全等的判定（四）
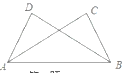
【题文】如图，在方格纸中，以AB为一边作△ABP，使之与△ABC全等，从P1，P2，P3，P4四个点中找出符合条件的点P，则点P有(   )
A．1个B．2个C．3个D．4个

【答案】

【解析】

登录学易云，内容更精彩！ 抱歉，未登录用户无法看答案与解析！

立即登录 还不是学易云用户？

题号：5114188 题型：选择题 难易度：一般 日期：2017-10-27 来源：浙教版八年级数学上册基础训练：1.5 三角形全等的判定（四）
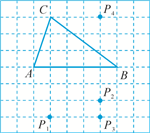
【题文】如图，已知AE⊥AB且AE＝AB，BC⊥CD且BC＝CD，按照图中所标注的数据，则图中阴影部分图形的面积S等于(  )
A．50B．62C．65D．68

【答案】

【解析】

登录学易云，内容更精彩！ 抱歉，未登录用户无法看答案与解析！

立即登录 还不是学易云用户？

题号：5114189 题型：选择题 难易度：一般 日期：2017-10-27 来源：浙教版八年级数学上册基础训练：1.5 三角形全等的判定（四）
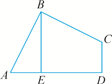
【题文】如图，在四边形ABCD中，AB＝BC，∠ABC＝∠CDA＝90°，BE⊥AD于点E，且四边形ABCD的面积为9，则BE＝(  )
A．2B．3C．4D．5

【答案】

【解析】

登录学易云，内容更精彩！ 抱歉，未登录用户无法看答案与解析！

立即登录 还不是学易云用户？

题号：5114183 题型：填空题 难易度：一般 日期：2017-10-27 来源：浙教版八年级数学上册基础训练：1.5 三角形全等的判定（四）
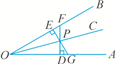
【题文】如图，P是∠AOB的平分线OC上的一点，PD⊥OA，PE⊥OB，垂足分别为D，E，延长DP交OB于点F，延长EP交OA于点G，则图中有____对全等三角形，它们分别是____．

【答案】

【解析】

登录学易云，内容更精彩！ 抱歉，未登录用户无法看答案与解析！

立即登录 还不是学易云用户？

题号：5114184 题型：填空题 难易度：一般 日期：2017-10-27 来源：浙教版八年级数学上册基础训练：1.5 三角形全等的判定（四）
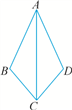
【题文】如图，∠B＝∠D，请添加一个条件(不得添加辅助线)，使得△ABC≌△ADC，你所添加的条件是________(只添一个即可)．

【答案】

【解析】

登录学易云，内容更精彩！ 抱歉，未登录用户无法看答案与解析！

立即登录 还不是学易云用户？

题号：5114185 题型：解答题 难易度：一般 日期：2017-10-27 来源：浙教版八年级数学上册基础训练：1.5 三角形全等的判定（四）
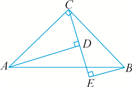
【题文】如图，在△ABC中，∠ACB＝90°，AC＝BC，AD⊥CE，BE⊥CE，D，E为垂足．求证：DE＋BE＝CE.

【答案】

【解析】

登录学易云，内容更精彩！ 抱歉，未登录用户无法看答案与解析！

立即登录 还不是学易云用户？

题号：5114186 题型：解答题 难易度：一般 日期：2017-10-27 来源：浙教版八年级数学上册基础训练：1.5 三角形全等的判定（四）
【题文】如图，已知点B，E，F，C在同一条直线上，∠A＝∠D，BE＝CF，且AB∥CD.求证：AF∥ED.

【答案】

【解析】

登录学易云，内容更精彩！ 抱歉，未登录用户无法看答案与解析！

立即登录 还不是学易云用户？

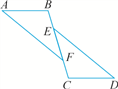
题号：5114187 题型：解答题 难易度：一般 日期：2017-10-27 来源：浙教版八年级数学上册基础训练：1.5 三角形全等的判定（四）
【题文】如图，在正方形ABCD中，G是BC上任意一点，连结AG，DE⊥AG于点E，BF∥DE交AG于点F，探究线段DE，BF，EF三者之间的数量关系，并说明理由．

【答案】

【解析】

登录学易云，内容更精彩！ 抱歉，未登录用户无法看答案与解析！

立即登录 还不是学易云用户？

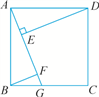
题号：5114190 题型：解答题 难易度：一般 日期：2017-10-27 来源：浙教版八年级数学上册基础训练：1.5 三角形全等的判定（四）
【题文】如图，在△ABC中，∠ABC＝90°，AB＝BC，三角形的顶点在相互平行的三条直线l1，l2，l3上，且l1，l2之间的距离为1，l2，l3之间的距离为2，过点A作AE⊥l3于点E，求BE的长．

【答案】

【解析】

登录学易云，内容更精彩！ 抱歉，未登录用户无法看答案与解析！

立即登录 还不是学易云用户？

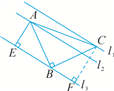
题号：5114191 题型：解答题 难易度：一般 日期：2015-03-06 来源：浙教版八年级数学上册基础训练：1.5 三角形全等的判定（四）
【题文】如图，在四边形ABCD中，AB∥DC，BE，CE分别平分∠ABC，∠BCD，且点E在AD上．求证：BC＝AB＋CD.

【答案】

【解析】

登录学易云，内容更精彩！ 抱歉，未登录用户无法看答案与解析！

立即登录 还不是学易云用户？

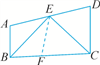
题号：5114192 题型：解答题 难易度：一般 日期：2017-10-27 来源：浙教版八年级数学上册基础训练：1.5 三角形全等的判定（四）
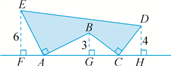
【题文】如图，在直角三角形ABC中，∠ACB＝90°，∠B＝60°，AD，CE是角平分线，AD与CE相交于点F，FM⊥AB，FN⊥BC，垂足分别为M，N.求证：FE＝FD.

【答案】

【解析】

登录学易云，内容更精彩！ 抱歉，未登录用户无法看答案与解析！

立即登录 还不是学易云用户？

热门推荐