适用年级:{{getGradeNameByProperty('初二|同步测试|全国|2012年')}} 试卷类型:{{getTestPaperTypeName('初二|同步测试|全国|2012年')}} 使用省份:{{getAreaName('初二|同步测试|全国|2012年')}}
试卷年份:{{getYear('初二|同步测试|全国|2012年')}}上传日期:2012-12-17题数:19
提示:单击题文可显示答案与解析。
题号:668619
题型:选择题
难易度:容易
日期:2012-12-17
来源:2012年沪科版初中数学八年级下18.1二次根式练习卷(带解析)
题号:668620
题型:选择题
难易度:较易
日期:2012-12-17
来源:2012年沪科版初中数学八年级下18.1二次根式练习卷(带解析)
【题文】
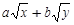
的有理化因式是
题号:668621
题型:选择题
难易度:较易
日期:2012-12-17
来源:2012年沪科版初中数学八年级下18.1二次根式练习卷(带解析)
【题文】把
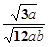
分母有理化后得
题号:668622
题型:选择题
难易度:较易
日期:2012-12-17
来源:2012年沪科版初中数学八年级下18.1二次根式练习卷(带解析)
【题文】对于二次根式
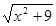
,以下说法不正确的是
| A.它是一个正数 | B.是一个无理数 |
| C.是最简二次根式 | D.它的最小值是3 |
题号:668623
题型:选择题
难易度:较易
日期:2012-12-17
来源:2012年沪科版初中数学八年级下18.1二次根式练习卷(带解析)
【题文】化简二次根式
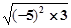
得
题号:668624
题型:选择题
难易度:较易
日期:2012-12-17
来源:2012年沪科版初中数学八年级下18.1二次根式练习卷(带解析)
题号:668625
题型:选择题
难易度:较易
日期:2012-12-17
来源:2012年沪科版初中数学八年级下18.1二次根式练习卷(带解析)
【题文】当
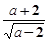
有意义时,a的取值范围是
题号:668626
题型:选择题
难易度:较易
日期:2012-12-17
来源:2012年沪科版初中数学八年级下18.1二次根式练习卷(带解析)
【题文】下列式子中二次根式的个数有
⑴
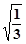
;⑵;⑶
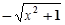
;⑷
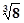
;⑸
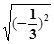
;⑹
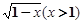
;⑺

.
题号:668627
题型:选择题
难易度:较易
日期:2012-12-17
来源:2012年沪科版初中数学八年级下18.1二次根式练习卷(带解析)
【题文】若

为二次根式,则m的取值为
题号:668628
题型:填空题
难易度:较易
日期:2012-12-17
来源:2012年沪科版初中数学八年级下18.1二次根式练习卷(带解析)
【题文】若
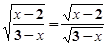
成立,则x满足_____________________.
题号:668629
题型:填空题
难易度:容易
日期:2012-12-17
来源:2012年沪科版初中数学八年级下18.1二次根式练习卷(带解析)
【题文】当a=
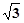
时,则
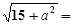
___________.
题号:668630
题型:填空题
难易度:较易
日期:2012-12-17
来源:2012年沪科版初中数学八年级下18.1二次根式练习卷(带解析)
【题文】计算:
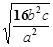
=_________________.
题号:668631
题型:填空题
难易度:较易
日期:2012-12-17
来源:2012年沪科版初中数学八年级下18.1二次根式练习卷(带解析)
【题文】计算:
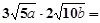
___________.
题号:668632
题型:填空题
难易度:较易
日期:2012-12-17
来源:2012年沪科版初中数学八年级下18.1二次根式练习卷(带解析)
【题文】
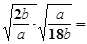
____________;
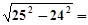
__________.
题号:668633
题型:填空题
难易度:较易
日期:2012-12-17
来源:2012年沪科版初中数学八年级下18.1二次根式练习卷(带解析)
【题文】比较大小:
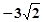
______
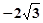
.
题号:668634
题型:填空题
难易度:较易
日期:2012-12-17
来源:2012年沪科版初中数学八年级下18.1二次根式练习卷(带解析)
【题文】当x___________时,
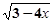
在实数范围内有意义.
题号:668635
题型:填空题
难易度:较易
日期:2012-12-17
来源:2012年沪科版初中数学八年级下18.1二次根式练习卷(带解析)
【题文】当x___________时,
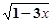
是二次根式.
题号:668617
题型:解答题
难易度:一般
日期:2012-12-17
来源:2012年沪科版初中数学八年级下18.1二次根式练习卷(带解析)
【题文】把下列各式化成最简二次根式:
⑴
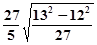
; ⑵
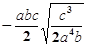
.
题号:668618
题型:解答题
难易度:较易
日期:2012-12-17
来源:2012年沪科版初中数学八年级下18.1二次根式练习卷(带解析)
【题文】把下列各式写成平方差的形式,再分解因式:
⑴
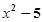
; ⑵
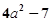
;
⑶
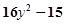
; ⑷
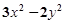
.
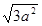
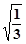
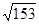
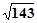
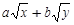 的有理化因式是
的有理化因式是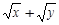
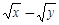
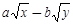
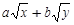
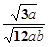 分母有理化后得
分母有理化后得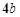
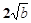

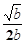
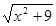 ,以下说法不正确的是
,以下说法不正确的是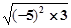 得
得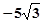
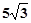
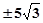
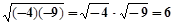 ;②
;②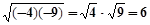 ;
;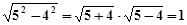 ;④
;④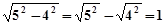 ;
;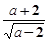 有意义时,a的取值范围是
有意义时,a的取值范围是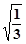 ;⑵;⑶
;⑵;⑶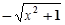 ;⑷
;⑷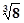 ;⑸
;⑸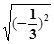 ;⑹
;⑹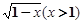 ;⑺
;⑺ .
. 为二次根式,则m的取值为
为二次根式,则m的取值为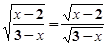 成立,则x满足_____________________.
成立,则x满足_____________________.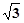 时,则
时,则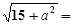 ___________.
___________.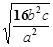 =_________________.
=_________________.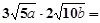 ___________.
___________.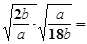 ____________;
____________;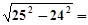 __________.
__________.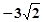 ______
______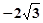 .
.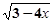 在实数范围内有意义.
在实数范围内有意义.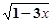 是二次根式.
是二次根式.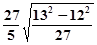 ; ⑵
; ⑵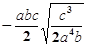 .
.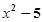 ; ⑵
; ⑵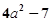 ;
;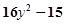 ; ⑷
; ⑷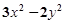 .
.