适用年级:{{getGradeNameByProperty('初一|同步测试|全国|2012年')}} 试卷类型:{{getTestPaperTypeName('初一|同步测试|全国|2012年')}} 使用省份:{{getAreaName('初一|同步测试|全国|2012年')}}
试卷年份:{{getYear('初一|同步测试|全国|2012年')}}上传日期:2012-10-22题数:31
提示:单击题文可显示答案与解析。
题号:675022
题型:选择题
难易度:较易
日期:2012-10-23
来源:2012年人教版七年级下第七章三角形第三节多边形及其内角和2练习卷(带解析)
【题文】不能镶嵌成平面图案的正多边形组合为( )
| A.正八边形和正方形 | B.正五边形和正十边形 |
| C.正六边形和正三角形 | D.正六边形和正八边形 |
题号:675095
题型:选择题
难易度:较易
日期:2012-10-22
来源:2012年人教版七年级下第七章三角形第三节多边形及其内角和2练习卷(带解析)
【题文】一个多边形有且只有三个内角是钝角,则n的最大值是( )
题号:675096
题型:选择题
难易度:较易
日期:2012-10-22
来源:2012年人教版七年级下第七章三角形第三节多边形及其内角和2练习卷(带解析)
【题文】每个内角都相等的多边形,它的一个外角等于一个内角的
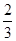
,则这个多边形是( )
题号:675097
题型:选择题
难易度:容易
日期:2012-10-22
来源:2012年人教版七年级下第七章三角形第三节多边形及其内角和2练习卷(带解析)
题号:3634171
题型:选择题
难易度:容易
日期:2013-05-10
来源:2012年人教版七年级下第七章三角形第三节多边形及其内角和2练习卷(带解析)
【题文】若多边形的边数由3增加到n(n为整数,且n>3)则其外角和的度数( )
题号:3634172
题型:选择题
难易度:较易
日期:2012-10-24
来源:2012年人教版七年级下第七章三角形第三节多边形及其内角和2练习卷(带解析)
【题文】用形状、大小完全相同的图形不能镶嵌成平面图案的是( )
题号:3634173
题型:选择题
难易度:较易
日期:2012-10-24
来源:2012年人教版七年级下第七章三角形第三节多边形及其内角和2练习卷(带解析)
题号:3634175
题型:选择题
难易度:较易
日期:2012-10-24
来源:2012年人教版七年级下第七章三角形第三节多边形及其内角和2练习卷(带解析)
【题文】如图所示,各边相等的五边形ABCDE中,若∠ABC=2∠DBE,则∠ABC等于( )
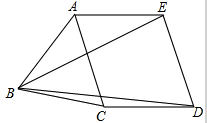
题号:3634176
题型:选择题
难易度:较易
日期:2012-10-24
来源:2012年人教版七年级下第七章三角形第三节多边形及其内角和2练习卷(带解析)
【题文】用正三角形和正六边形镶嵌,若每一个顶点周围有m个正三角形、n 个正六边形,则m,n满足的关系式是( )
| A.2m+3n=12 | B.m+n=8 | C.2m+n=6 | D.m+2n=6 |
题号:3657760
题型:单选题
难易度:较易
日期:2017-05-17
来源:2012年人教版七年级下第七章三角形第三节多边形及其内角和2练习卷(带解析)
【题文】已知一个多边形的外角和是内角和的2倍,则这个多边形是( )
题号:675016
题型:填空题
难易度:容易
日期:2012-10-23
来源:2012年人教版七年级下第七章三角形第三节多边形及其内角和2练习卷(带解析)
【题文】用一种正五边形或正八边形的瓷砖_______铺满地面.(填“能”或“不能”)
题号:675017
题型:填空题
难易度:较易
日期:2012-10-23
来源:2012年人教版七年级下第七章三角形第三节多边形及其内角和2练习卷(带解析)
【题文】用正多边形镶嵌,设在一个顶点周围有m个正方形、n个正八边形,则m=_____,n=______.
题号:675090
题型:填空题
难易度:较易
日期:2012-10-22
来源:2012年人教版七年级下第七章三角形第三节多边形及其内角和2练习卷(带解析)
【题文】若一个多边形各边均相等,周长为
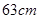
,且内角和为900º,则它的边长为
.
题号:675091
题型:填空题
难易度:容易
日期:2012-10-22
来源:2012年人教版七年级下第七章三角形第三节多边形及其内角和2练习卷(带解析)
【题文】已知∠A的两边与∠B的两边互相垂直,若∠A=80º,则∠B的度数是 .
题号:675092
题型:填空题
难易度:容易
日期:2012-10-22
来源:2012年人教版七年级下第七章三角形第三节多边形及其内角和2练习卷(带解析)
题号:675093
题型:填空题
难易度:较易
日期:2012-10-22
来源:2012年人教版七年级下第七章三角形第三节多边形及其内角和2练习卷(带解析)
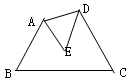
【题文】如图,四边形ABCD中,AE平分∠BAD,DE平分∠ADC,且∠ABC=80º,∠BCD=70º,则∠AED=
.
题号:675094
题型:填空题
难易度:较易
日期:2012-10-22
来源:2012年人教版七年级下第七章三角形第三节多边形及其内角和2练习卷(带解析)
【题文】一个五边形有三个内角是直角,另两个都等于nº,则n的值是 .
题号:3634177
题型:填空题
难易度:较易
日期:2012-10-23
来源:2012年人教版七年级下第七章三角形第三节多边形及其内角和2练习卷(带解析)
【题文】一个多边形的每个外角都等于36º,则这个多边形的内角和是 度.
题号:3634178
题型:填空题
难易度:较易
日期:2012-10-24
来源:2012年人教版七年级下第七章三角形第三节多边形及其内角和2练习卷(带解析)
【题文】用正三角形和正六边形镶嵌,在每个顶点处有_______个正三角形和_____ 个正六边形,或在每个顶点处有______个正三角形和________个正六边形.
题号:3634181
题型:填空题
难易度:较易
日期:2012-12-18
来源:2012年人教版七年级下第七章三角形第三节多边形及其内角和2练习卷(带解析)
【题文】如果一个多边形的每一个外角都小于45º,这样的多边形边数的最小值是 .
题号:675013
题型:解答题
难易度:较易
日期:2012-10-23
来源:2012年人教版七年级下第七章三角形第三节多边形及其内角和2练习卷(带解析)
【题文】请你设计在每一个顶点处由四个正多边形拼成的平面图案, 你能设计出多少种不同的方案?
题号:675014
题型:解答题
难易度:较易
日期:2012-10-23
来源:2012年人教版七年级下第七章三角形第三节多边形及其内角和2练习卷(带解析)
【题文】用一个正方形、一个正五边形、一个正二十边形能否镶嵌成平面图案? 说明理由.
题号:675082
题型:解答题
难易度:较易
日期:2012-10-22
来源:2012年人教版七年级下第七章三角形第三节多边形及其内角和2练习卷(带解析)
【题文】某同学采用把多边形内角逐个相加的方法计算多边形的内角和,求得一个多边形的内角和为
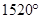
,当他发现错了以后,重新检查,发现少加了一个内角.问:这个内角是多少度?他求的这个多边形的边数是多少?
题号:675083
题型:解答题
难易度:较易
日期:2012-10-22
来源:2012年人教版七年级下第七章三角形第三节多边形及其内角和2练习卷(带解析)
【题文】一个多边形的内角度数从小到大排列起来,恰好依次增加相同的度数,其中最小角是
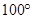
,最大角是
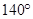
,求这个多边形的边数.
题号:675084
题型:解答题
难易度:较易
日期:2012-10-22
来源:2012年人教版七年级下第七章三角形第三节多边形及其内角和2练习卷(带解析)
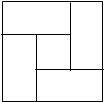
【题文】如图,若用4块相同的长方形瓷砖拼成一个大正方形面积为
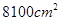
,中间空一个小正方形面积为
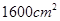
,求长方形瓷砖的长和宽.
题号:675085
题型:解答题
难易度:较易
日期:2012-10-22
来源:2012年人教版七年级下第七章三角形第三节多边形及其内角和2练习卷(带解析)
题号:675086
题型:解答题
难易度:较易
日期:2012-10-22
来源:2012年人教版七年级下第七章三角形第三节多边形及其内角和2练习卷(带解析)
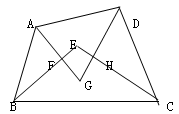
【题文】如图,四边形ABCD中,各内角的平分线所围成的四边形为EFGH,求∠E+∠G的度数.
题号:675087
题型:解答题
难易度:一般
日期:2012-10-22
来源:2012年人教版七年级下第七章三角形第三节多边形及其内角和2练习卷(带解析)
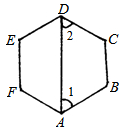
【题文】如图,六边形ABCDEF各内角相等,∠1=∠2=60°,AB与DE有怎样的位置关系?AD与BC有怎样的位置关系?为什么?
题号:675088
题型:解答题
难易度:较易
日期:2012-10-22
来源:2012年人教版七年级下第七章三角形第三节多边形及其内角和2练习卷(带解析)
【题文】某家庭准备用正三角形和正六边形两种瓷砖结合在一起镶嵌地面,由你帮助设计镶嵌图案,你能设计几种不同的镶嵌方案?
题号:675089
题型:解答题
难易度:较易
日期:2012-10-22
来源:2012年人教版七年级下第七章三角形第三节多边形及其内角和2练习卷(带解析)
【题文】一个多边形的各个内角都相等,每个内角与外角的差为36º,求这个多边形的边数.
题号:3634182
题型:解答题
难易度:较易
日期:2012-10-24
来源:2012年人教版七年级下第七章三角形第三节多边形及其内角和2练习卷(带解析)
【题文】计算用一种正多边形拼成平整、无隙的图案,你能设计出几种方案?画出草图.
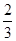 ,则这个多边形是( )
,则这个多边形是( )
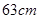 ,且内角和为900º,则它的边长为 .
,且内角和为900º,则它的边长为 .
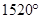 ,当他发现错了以后,重新检查,发现少加了一个内角.问:这个内角是多少度?他求的这个多边形的边数是多少?
,当他发现错了以后,重新检查,发现少加了一个内角.问:这个内角是多少度?他求的这个多边形的边数是多少?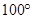 ,最大角是
,最大角是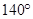 ,求这个多边形的边数.
,求这个多边形的边数.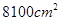 ,中间空一个小正方形面积为
,中间空一个小正方形面积为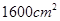 ,求长方形瓷砖的长和宽.
,求长方形瓷砖的长和宽.
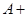 ∠
∠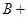 ∠
∠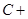 ∠
∠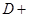 ∠
∠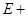 ∠
∠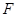 的度数.
的度数.

