 -
- =1(a>0,b>0)的离心率为2,一个焦点与抛物线y2=16x的焦点相同,则双曲线的渐近线方程为( )
=1(a>0,b>0)的离心率为2,一个焦点与抛物线y2=16x的焦点相同,则双曲线的渐近线方程为( )A.y=±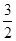 x x | B.y=±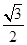 x x |
C.y=±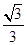 x x | D.y=±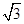 x x |
 -
- =1(a>0,b>0)的渐近线没有公共点,则此双曲线的离心率可以是( )
=1(a>0,b>0)的渐近线没有公共点,则此双曲线的离心率可以是( )A.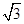 | B.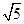 | C.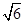 | D.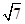 |
 -
- =1(a>0,b>0)的左焦点F引圆x2+y2=a2的切线,切点为T,延长FT交双曲线右支于点P,若T为线段FP的中点,则该双曲线的渐近线方程为( )
=1(a>0,b>0)的左焦点F引圆x2+y2=a2的切线,切点为T,延长FT交双曲线右支于点P,若T为线段FP的中点,则该双曲线的渐近线方程为( )| A.x±y=0 | B.2x±y=0 |
| C.4x±y=0 | D.x±2y=0 |
 -y2=1(a>0)交于A、B两点,若△FAB为直角三角形,则双曲线的离心率为( )
-y2=1(a>0)交于A、B两点,若△FAB为直角三角形,则双曲线的离心率为( )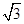 (B)
(B) 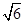 (C)2 (D)
(C)2 (D)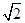 +1
+1 -
- =1(a>0,b>0)的左顶点与抛物线y2=2px(p>0)的焦点的距离为4,且双曲线的一条渐近线与抛物线的准线的交点坐标为(-2,-1),则双曲线的焦距为( )
=1(a>0,b>0)的左顶点与抛物线y2=2px(p>0)的焦点的距离为4,且双曲线的一条渐近线与抛物线的准线的交点坐标为(-2,-1),则双曲线的焦距为( )A.2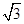 | B.2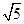 | C.4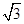 | D.4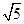 |
 -
- =1(a>0,b>0)的离心率为2.若抛物线C2:x2=2py(p>0)的焦点到双曲线C1的渐近线的距离为2,则抛物线C2的方程为( )
=1(a>0,b>0)的离心率为2.若抛物线C2:x2=2py(p>0)的焦点到双曲线C1的渐近线的距离为2,则抛物线C2的方程为( )A.x2=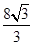 y y | B.x2=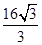 y y |
| C.x2=8y | D.x2=16y |
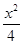 -
-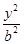 =1的右焦点与抛物线y2=12x的焦点重合,则该双曲线的焦点到其渐近线的距离等于()
=1的右焦点与抛物线y2=12x的焦点重合,则该双曲线的焦点到其渐近线的距离等于()A.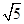 | B.4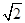 | C.3 | D.5 |
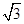 ,则C的实轴长为( )
,则C的实轴长为( )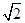 (B)2
(B)2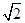 (C)4 (D)8
(C)4 (D)8 +
+ =1(a>b>0)与双曲线C2:x2-
=1(a>b>0)与双曲线C2:x2-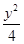 =1有公共的焦点,C2的一条渐近线与以C1的长轴为直径的圆相交于A,B两点.若C1恰好将线段AB三等分,则( )
=1有公共的焦点,C2的一条渐近线与以C1的长轴为直径的圆相交于A,B两点.若C1恰好将线段AB三等分,则( )A.a2=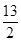 | B.a2=13 |
C.b2=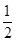 | D.b2=2 |
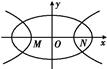
| A.3 | B.2 | C.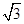 | D.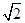 |
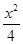 +y2=1与双曲线C2的公共焦点,A,B分别是C1,C2在第二、四象限的公共点.若四边形AF1BF2为矩形,则C2的离心率是( )
+y2=1与双曲线C2的公共焦点,A,B分别是C1,C2在第二、四象限的公共点.若四边形AF1BF2为矩形,则C2的离心率是( )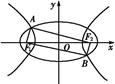
A.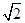 | B.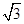 | C.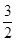 | D.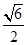 |
 +
+ =1(a>b>0)的离心率为
=1(a>b>0)的离心率为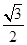 .双曲线x2-y2=1的渐近线与椭圆C有四个交点,以这四个交点为顶点的四边形的面积为16,则椭圆C的方程为( )
.双曲线x2-y2=1的渐近线与椭圆C有四个交点,以这四个交点为顶点的四边形的面积为16,则椭圆C的方程为( )A.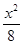 + +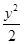 =1 =1 | B.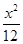 + +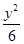 =1 =1 |
C.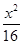 + +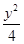 =1 =1 | D.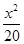 + +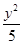 =1 =1 |
 -
- =1(a>0,b>0)的一条渐近线方程是y=
=1(a>0,b>0)的一条渐近线方程是y=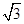 x,它的一个焦点在抛物线y2=24x的准线上,则双曲线的方程为( )
x,它的一个焦点在抛物线y2=24x的准线上,则双曲线的方程为( )A.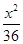 - -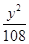 =1 =1 | B.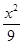 - -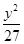 =1 =1 |
C.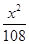 - -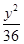 =1 =1 | D.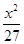 - -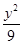 =1 =1 |
 -
- =1的一条渐近线与抛物线y=x2+1只有一个公共点,则双曲线的离心率为( )
=1的一条渐近线与抛物线y=x2+1只有一个公共点,则双曲线的离心率为( )A.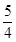 | B.5 | C.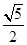 | D.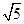 |
 +
+ =1(a>b>0)的焦点垂直于x轴的弦长为
=1(a>b>0)的焦点垂直于x轴的弦长为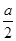 ,则双曲线
,则双曲线 -
- =1的离心率e的值是( )
=1的离心率e的值是( )A.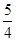 | B.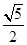 |
C.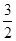 | D.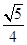 |
 -
- =1(a>0,b>0)的一条渐近线的交点,若点A到抛物线C1的准线的距离为p,则双曲线C2的离心率等于( )
=1(a>0,b>0)的一条渐近线的交点,若点A到抛物线C1的准线的距离为p,则双曲线C2的离心率等于( )A.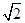 | B.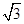 | C.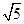 | D.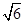 |
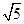 ,则抛物线的方程为( )
,则抛物线的方程为( )| A.y2=4x | B.x2=4y |
| C.y2=8x | D.x2=8y |
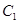 :
: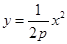
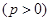 的焦点与双曲线
的焦点与双曲线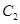 :
: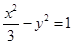 的右焦点的连线交
的右焦点的连线交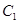 于第一象限的点
于第一象限的点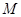 ,若
,若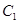 在点
在点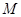 处的切线平行于
处的切线平行于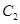 的一条渐近线,则
的一条渐近线,则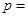 ()
()A.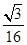 | B.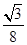 | C.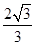 | D.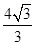 |
 +
+ =1(a>b>0)与抛物线y2=2px(p>0)有相同的焦点,P、Q是椭圆与抛物线的交点,若PQ经过焦点F,则椭圆
=1(a>b>0)与抛物线y2=2px(p>0)有相同的焦点,P、Q是椭圆与抛物线的交点,若PQ经过焦点F,则椭圆 +
+ =1(a>b>0)的离心率为 .
=1(a>b>0)的离心率为 .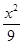 +
+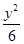 =1和C2:x2-
=1和C2:x2-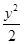 =1在第二象限的交点,B、C为曲线C1的左、右焦点,线段BC上一点P满足:
=1在第二象限的交点,B、C为曲线C1的左、右焦点,线段BC上一点P满足: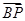 =
=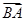 +m(
+m(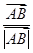 +
+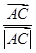 ),则实数m的值为 .
),则实数m的值为 . -
- =1(a>0,b>0)的一个焦点,且双曲线的离心率为2,则该双曲线的方程为 .
=1(a>0,b>0)的一个焦点,且双曲线的离心率为2,则该双曲线的方程为 . -
- =1(a>0,b>0)的一条渐近线方程是y=
=1(a>0,b>0)的一条渐近线方程是y=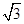 x,它的一个焦点与抛物线y2=16x的焦点相同,则双曲线的方程为 .
x,它的一个焦点与抛物线y2=16x的焦点相同,则双曲线的方程为 . -
- =1(a>0,b>0)和椭圆
=1(a>0,b>0)和椭圆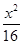 +
+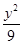 =1有相同的焦点,且双曲线的离心率是椭圆离心率的两倍,则双曲线的方程为 .
=1有相同的焦点,且双曲线的离心率是椭圆离心率的两倍,则双曲线的方程为 . +
+ =1的左、右顶点,P是椭圆上异于A,B的任意一点,Q是双曲线C2:
=1的左、右顶点,P是椭圆上异于A,B的任意一点,Q是双曲线C2: -
- =1上异于A,B的任意一点,a>b>0.
=1上异于A,B的任意一点,a>b>0.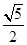 ,
,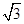 ),Q(
),Q(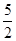 ,1),求椭圆C1的方程;
,1),求椭圆C1的方程; +
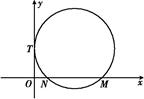
+ =1(a>b>0)的焦距等于2|ON|,且过点(
=1(a>b>0)的焦距等于2|ON|,且过点(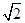 ,
,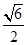 ).
).
 +
+ =1(a>b>0),以抛物线y2=8x的焦点为顶点,且离心率为
=1(a>b>0),以抛物线y2=8x的焦点为顶点,且离心率为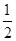 .
.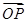 =
=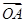 +
+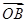 ,证明
,证明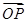 ·
·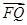 为定值,并求出该值.
为定值,并求出该值.
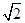 ,0),(
,0),(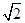 ,0),离心率是
,0),离心率是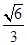 .直线y=t与椭圆C交于不同的两点M,N,以线段MN为直径作圆P,圆心为P.
.直线y=t与椭圆C交于不同的两点M,N,以线段MN为直径作圆P,圆心为P.
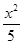 +y2=1的左、右焦点,F1,F2关于直线x+y-2=0的对称点是圆C的一条直径的两个端点.
+y2=1的左、右焦点,F1,F2关于直线x+y-2=0的对称点是圆C的一条直径的两个端点.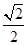 ,过左焦点F1作x轴的垂线交椭圆于A、A′两点,
,过左焦点F1作x轴的垂线交椭圆于A、A′两点,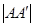 =4.
=4.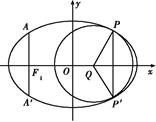
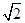 ,在y轴上截得线段长为2
,在y轴上截得线段长为2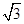 .
.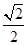 ,求圆P的方程.
,求圆P的方程.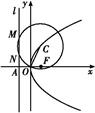
 +
+ =1(a>b>0)的右顶点为A(1,0),过C1的焦点且垂直长轴的弦长为1.
=1(a>b>0)的右顶点为A(1,0),过C1的焦点且垂直长轴的弦长为1.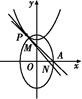
 +
+ =1(a>b>0)的两个焦点.
=1(a>b>0)的两个焦点.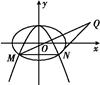
 +
+ =1(a>b>0),抛物线C2:x2+by=b2.
=1(a>b>0),抛物线C2:x2+by=b2.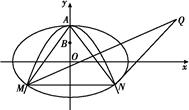
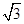 ,
,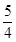 b),又M,N为C1与C2不在y轴上的两个交点,若△AMN的垂心为B(0,
b),又M,N为C1与C2不在y轴上的两个交点,若△AMN的垂心为B(0,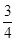 b),且△QMN的重心在C2上,求椭圆C1和抛物线C2的方程.
b),且△QMN的重心在C2上,求椭圆C1和抛物线C2的方程.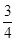 .
.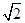 ,直线l:y=kx+
,直线l:y=kx+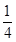 与抛物线C有两个不同的交点A,B,l与圆Q有两个不同的交点D,E,求当
与抛物线C有两个不同的交点A,B,l与圆Q有两个不同的交点D,E,求当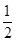 ≤k≤2时,|AB|2+|DE|2的最小值.
≤k≤2时,|AB|2+|DE|2的最小值. +
+ =1(a>b>0)的左焦点为F1(-1,0),且点P(0,1)在C1上.
=1(a>b>0)的左焦点为F1(-1,0),且点P(0,1)在C1上.