适用年级:{{getGradeNameByProperty('高三|专题试卷|全国|2014年')}} 试卷类型:{{getTestPaperTypeName('高三|专题试卷|全国|2014年')}} 使用省份:{{getAreaName('高三|专题试卷|全国|2014年')}}
试卷年份:{{getYear('高三|专题试卷|全国|2014年')}}上传日期:2014-04-05题数:12
提示:单击题文可显示答案与解析。
题号:939798
题型:选择题
难易度:一般
日期:2014-04-05
来源:2014年高考数学(文)二轮专题复习与测试专题1第5课时练习卷(带解析)
【题文】已知f(x)=x
3-6x
2+9x-abc,a<b<c,且f(a)=f(b)=f(c)=0.现给出如下结论:
①f(0)f(1)>0;②f(0)f(1)<0;③f(0)f(3)>0;
④f(0)f(3)<0.
其中正确结论的序号是( )
题号:939799
题型:选择题
难易度:一般
日期:2014-04-05
来源:2014年高考数学(文)二轮专题复习与测试专题1第5课时练习卷(带解析)
【题文】设函数f(x)的定义域为R,x
0(x
0≠0)是f(x)的极大值点,以下结论一定正确的是( )
| A.∀x∈R,f(x)≤f(x0) |
| B.-x0是f(-x)的极小值点 |
| C.-x0是-f(x)的极小值点 |
| D.-x0是-f(-x)的极小值点 |
题号:939800
题型:选择题
难易度:一般
日期:2014-04-05
来源:2014年高考数学(文)二轮专题复习与测试专题1第5课时练习卷(带解析)
【题文】函数f(x)的定义域是R,f(0)=2,对任意x∈R,f(x)+f ′(x)>1,则不等式e
x·f(x)>e
x+1
的解集为( )
| A.{x|x>0} |
| B.{x|x<0} |
| C.{x|x<-1,或x>1} |
| D.{x|x<-1,或0<x<1} |
题号:939801
题型:选择题
难易度:一般
日期:2014-04-05
来源:2014年高考数学(文)二轮专题复习与测试专题1第5课时练习卷(带解析)
【题文】函数f(x)的定义域为(0,+∞),且f(x)>0,f′(x)>0,则函数y=xf(x)( )
| A.存在极大值 | B.存在极小值 |
| C.是增函数 | D.是减函数 |
题号:939802
题型:选择题
难易度:一般
日期:2014-04-05
来源:2014年高考数学(文)二轮专题复习与测试专题1第5课时练习卷(带解析)
【题文】已知e为自然对数的底数,则函数y=xe
x的单调递增区间是( )
| A.[-1,+∞) | B.(-∞,-1] |
| C.[1,+∞) | D.(-∞,1] |
题号:939803
题型:选择题
难易度:较易
日期:2014-04-05
来源:2014年高考数学(文)二轮专题复习与测试专题1第5课时练习卷(带解析)
【题文】已知曲线f(x)=ln x在点(x
0,f(x
0))处的切线经过点(0,-1),则x
0的值为( )
A.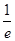 | B.1 |
| C.e | D.10 |
题号:939795
题型:填空题
难易度:一般
日期:2014-04-05
来源:2014年高考数学(文)二轮专题复习与测试专题1第5课时练习卷(带解析)
【题文】设函数y=f(x),x∈R的导函数为f′(x),且f(x)=f(-x),f′(x)<f(x).则下列三个数:ef(2),f(3),e2f(-1)从小到大依次排列为________.(e为自然对数的底数)
题号:939796
题型:填空题
难易度:一般
日期:2014-04-05
来源:2014年高考数学(文)二轮专题复习与测试专题1第5课时练习卷(带解析)
【题文】若函数f(x)=
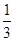
x
3-
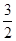
x
2+ax+4恰在[-1,4]上单调递减,则实数a的值为________.
题号:939797
题型:填空题
难易度:一般
日期:2014-04-05
来源:2014年高考数学(文)二轮专题复习与测试专题1第5课时练习卷(带解析)
【题文】函数f(x)=
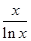
的单调递减区间是________.
题号:939792
题型:解答题
难易度:一般
日期:2014-04-05
来源:2014年高考数学(文)二轮专题复习与测试专题1第5课时练习卷(带解析)
【题文】已知函数f(x)=ln x+ax(a∈R).
(1)求f(x)的单调区间;
(2)设g(x)=x2-4x+2,若对任意x1∈(0,+∞),均存在x2∈[0,1],使得f(x1)<g(x2),求a的取值范围.
题号:939793
题型:解答题
难易度:一般
日期:2014-04-05
来源:2014年高考数学(文)二轮专题复习与测试专题1第5课时练习卷(带解析)
【题文】已知函数f(x)=
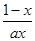
+ln x.
(1)当a=
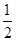
时,求f(x)在[1,e]上的最大值和最小值;
(2)若函数g(x)=f(x)-
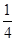
x在[1,e]上为增函数,求正实数a的取值范围.
题号:939794
题型:解答题
难易度:一般
日期:2014-04-05
来源:2014年高考数学(文)二轮专题复习与测试专题1第5课时练习卷(带解析)
【题文】设f(x)=aln x+
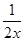
+
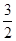
x+1,其中a∈R,曲线y=f(x)在点(1,f(1))处的切线垂直于y轴.
(1)求a的值;
(2)求函数f(x)的极值.
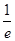
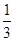 x3-
x3-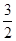 x2+ax+4恰在[-1,4]上单调递减,则实数a的值为________.
x2+ax+4恰在[-1,4]上单调递减,则实数a的值为________.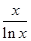 的单调递减区间是________.
的单调递减区间是________.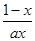 +ln x.
+ln x.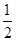 时,求f(x)在[1,e]上的最大值和最小值;
时,求f(x)在[1,e]上的最大值和最小值;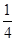 x在[1,e]上为增函数,求正实数a的取值范围.
x在[1,e]上为增函数,求正实数a的取值范围.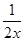 +
+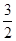 x+1,其中a∈R,曲线y=f(x)在点(1,f(1))处的切线垂直于y轴.
x+1,其中a∈R,曲线y=f(x)在点(1,f(1))处的切线垂直于y轴.