适用年级:{{getGradeNameByProperty('高三|专题试卷|全国|2014年')}} 试卷类型:{{getTestPaperTypeName('高三|专题试卷|全国|2014年')}} 使用省份:{{getAreaName('高三|专题试卷|全国|2014年')}}
试卷年份:{{getYear('高三|专题试卷|全国|2014年')}}上传日期:2014-03-17题数:11
提示:单击题文可显示答案与解析。
题号:948367
题型:选择题
难易度:一般
日期:2014-03-17
来源:2014年高考数学(理)二轮专题复习知能提升演练1-7-2练习卷(带解析)
【题文】设随机变量
ξ服从正态分布
N(
μ,
σ2),函数
f(
x)=
x2+4
x+
ξ没有零点的概率是
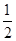
,则
μ= ( ).
题号:948368
题型:选择题
难易度:较易
日期:2014-03-17
来源:2014年高考数学(理)二轮专题复习知能提升演练1-7-2练习卷(带解析)
【题文】连掷两次骰子得到的点数分别为
m和
n,记向量
a=(
m,
n)与向量
b=(1,-1)的夹角为
θ.则
θ∈
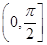
的概率是( ).
题号:4187705
题型:选择题
难易度:较易
日期:2014-03-21
来源:2014年高考数学(理)二轮专题复习知能提升演练1-7-2练习卷(带解析)
【题文】在长为12 cm的线段
AB上任取一点
C.现作一矩形,邻边长分别等于线段
AC,
CB的长,则该矩形面积小于32 cm
2的概率为( ).
题号:4187706
题型:选择题
难易度:较易
日期:2014-03-21
来源:2014年高考数学(理)二轮专题复习知能提升演练1-7-2练习卷(带解析)
【题文】如图所示,在边长为1的正方形
OABC中任取一点
P,则点
P恰好取自阴影部分的概率为( ).
题号:4187707
题型:选择题
难易度:一般
日期:2014-03-21
来源:2014年高考数学(理)二轮专题复习知能提升演练1-7-2练习卷(带解析)
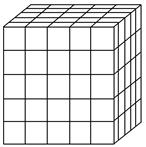
【题文】如图,将一个各面都涂了油漆的正方体,切割为125个同样大小的小正方体,经过搅拌后,从中随机取一个小正方体,记它的油漆面数为X,则X的均值
E(X)等于( ).
题号:948366
题型:填空题
难易度:一般
日期:2014-03-17
来源:2014年高考数学(理)二轮专题复习知能提升演练1-7-2练习卷(带解析)
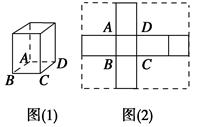
【题文】如图所示,图(2)中实线围成的部分是长方体(图(1))的平面展开图,其中四边形
ABCD是边长为1的正方形.若向虚线围成的矩形内任意抛掷一质点.它落在长方体的平面展开图内的概率是
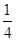
,则此长方体的体积是________.
题号:4187708
题型:填空题
难易度:较易
日期:2014-03-21
来源:2014年高考数学(理)二轮专题复习知能提升演练1-7-2练习卷(带解析)
【题文】从
n个正整数1,2,…,
n中任意取出两个不同的数,若取出的两数之和等于5的概率为
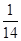
,则
n=________.
题号:4187709
题型:填空题
难易度:一般
日期:2014-03-21
来源:2014年高考数学(理)二轮专题复习知能提升演练1-7-2练习卷(带解析)
【题文】设非零常数d是等差数列x1,x2,x3,…,x19的公差,随机变量ξ等可能地取值x1,x2,x3,…,x19,则方差D(ξ)=________.
题号:948365
题型:解答题
难易度:一般
日期:2014-03-17
来源:2014年高考数学(理)二轮专题复习知能提升演练1-7-2练习卷(带解析)
【题文】一个盒子里装有7张卡片,其中有红色卡片4张,编号分别为1,2,3,4;白色卡片3张,编号分别为2,3,4.从盒子中任取4张卡片(假设取到任何一张卡片的可能性相同).
(1)求取出的4张卡片中,含有编号为3的卡片的概率;
(2)在取出的4张卡片中,红色卡片编号的最大值设为X,求随机变量X的分布列和数学期望.
题号:4187710
题型:解答题
难易度:一般
日期:2014-03-21
来源:2014年高考数学(理)二轮专题复习知能提升演练1-7-2练习卷(带解析)
【题文】假设某班级教室共有4扇窗户,在每天上午第三节课上课预备铃声响起时,每扇窗户或被敞开或被关闭,且概率均为0.5.记此时教室里敞开的窗户个数为X.
(1)求X的分布列;
(2)若此时教室里有两扇或两扇以上的窗户被关闭,班长就会将关闭的窗户全部敞开,否则维持原状不变.记每天上午第三节课上课时该教室里敞开的窗户个数为Y,求Y的数学期望.
题号:4187711
题型:解答题
难易度:较难
日期:2014-03-21
来源:2014年高考数学(理)二轮专题复习知能提升演练1-7-2练习卷(带解析)
【题文】设袋子中装有
a个红球,
b个黄球,
c个蓝球,且规定:取出一个红球得1分,取出一个黄球得2分,取出一个蓝球得3分.
(1)当
a=3,
b=2,
c=1时,从该袋子中任取(有放回,且每球取到的机会均等)2个球,记随机变量
ξ为取出此2球所得分数之和,求
ξ的分布列;
(2)从该袋子中任取(每球取到的机会均等)1个球,记随机变量
η为取出此球所得分数.若
E(
η)=
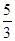
,
D(
η)=
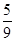
,求
a∶
b∶
c.
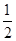 ,则μ= ( ).
,则μ= ( ).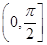 的概率是( ).
的概率是( ).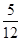
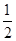
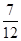
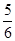
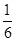
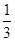
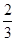
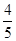
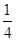
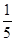
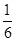
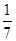

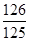
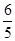
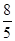
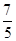
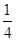 ,则此长方体的体积是________.
,则此长方体的体积是________.
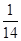 ,则n=________.
,则n=________.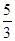 ,D(η)=
,D(η)=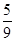 ,求a∶b∶c.
,求a∶b∶c.