适用年级:{{getGradeNameByProperty('初三|中考模拟|浙江|2014年')}} 试卷类型:{{getTestPaperTypeName('初三|中考模拟|浙江|2014年')}} 使用省份:{{getAreaName('初三|中考模拟|浙江|2014年')}}
试卷年份:{{getYear('初三|中考模拟|浙江|2014年')}}上传日期:2014-04-29题数:10
提示:单击题文可显示答案与解析。
题号:639208
题型:选择题
难易度:较易
日期:2014-04-29
来源:2014届新人教版初中数学浙江永嘉桥下瓯渠中学中考总复习第十八讲练习卷(带解析)
【题文】一件工艺品进价为100元,标价135元售出,每天可售出100件.根据销售统计,一件工艺品每降价1元出售,则每天可多售出4件,要使每天获得的利润最大,每件需降价的钱数为( )
题号:639209
题型:选择题
难易度:较易
日期:2014-04-29
来源:2014届新人教版初中数学浙江永嘉桥下瓯渠中学中考总复习第十八讲练习卷(带解析)
【题文】为搞好环保,某公司准备修建一个长方体的污水处理池,池底矩形的周长为100 m,则池底的最大面积是( )
| A.600 m2 | B.625 m2 | C.650 m2 | D.675 m2 |
题号:639210
题型:选择题
难易度:一般
日期:2014-04-29
来源:2014届新人教版初中数学浙江永嘉桥下瓯渠中学中考总复习第十八讲练习卷(带解析)
题号:3562726
题型:选择题
难易度:一般
日期:2014-04-30
来源:2014届新人教版初中数学浙江永嘉桥下瓯渠中学中考总复习第十八讲练习卷(带解析)
【题文】竖直向上发射的小球的高度h(m)关于运动时间t(s)的函数表达式为h=at
2+bt,其图象如图所示,若小球在发射后第2秒与第6秒时的高度相等,则下列时刻中小球的高度最高的是( )
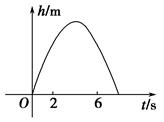
| A.第3秒 | B.第3.5秒 |
| C.第4.2秒 | D.第6.5秒 |
题号:639207
题型:填空题
难易度:较易
日期:2014-04-29
来源:2014届新人教版初中数学浙江永嘉桥下瓯渠中学中考总复习第十八讲练习卷(带解析)
【题文】某一型号飞机着陆后滑行的距离y(单位:m)与滑行时间x(单位:s)之间的函数关系式是y=60x-1.5x2,该型号飞机着陆后滑行________m才能停下来.
题号:3562725
题型:填空题
难易度:较易
日期:2014-04-30
来源:2014届新人教版初中数学浙江永嘉桥下瓯渠中学中考总复习第十八讲练习卷(带解析)
【题文】某广场有一喷水池,水从地面喷出,如图,以水平地面为x轴,出水点为原点,建立平面直角坐标系,水在空中划出的曲线是抛物线y=-x
2+4x(单位:米)的一部分,则水喷出的最大高度是( )
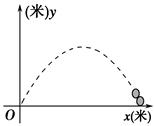
题号:3562727
题型:填空题
难易度:较易
日期:2014-04-30
来源:2014届新人教版初中数学浙江永嘉桥下瓯渠中学中考总复习第十八讲练习卷(带解析)
【题文】教练对小明推铅球的录像进行技术分析,发现铅球行进高度y(m)与水平距离x(m)之间的关系为y=-
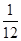
(x-4)
2+3,由此可知铅球推出的距离是________m.

题号:639206
题型:解答题
难易度:一般
日期:2014-04-29
来源:2014届新人教版初中数学浙江永嘉桥下瓯渠中学中考总复习第十八讲练习卷(带解析)
【题文】如图,某种新型导弹从地面发射点L处发射,在初始竖直加速飞行阶段,导弹上升的高度y(km)与飞行时间x(s)之间的关系式为y=
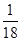
x
2+
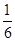
x(0≤x≤10).发射3 s后,导弹到达A点,此时位于与L同一水面的R处雷达站测得AR的距离是2 km,再过3 s后,导弹到达B点.
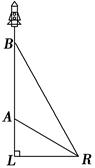
(1)求发射点L与雷达站R之间的距离;
(2)当导弹到达B点时,求雷达站测得的仰角(即∠BRL)的正切值.
题号:3562728
题型:解答题
难易度:一般
日期:2014-04-30
来源:2014届新人教版初中数学浙江永嘉桥下瓯渠中学中考总复习第十八讲练习卷(带解析)
【题文】如图,矩形ABCD的两边长AB=18 cm,AD=4 cm,点P、Q分别从A、B同时出发,P在边AB上沿AB方向以每秒2 cm的速度匀速运动,Q在边BC上沿BC方向以每秒1 cm的速度匀速运动.设运动时间为x秒,△PBQ的面积为y(cm
2).
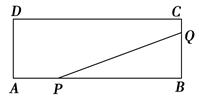
(1)求y关于x的函数关系式,并写出x的取值范围;
(2)求△PBQ的面积的最大值.
题号:3562729
题型:解答题
难易度:一般
日期:2014-04-30
来源:2014届新人教版初中数学浙江永嘉桥下瓯渠中学中考总复习第十八讲练习卷(带解析)
【题文】如图,排球运动员站在点O处练习发球,将球从O点正上方2 m的A处发出,把球看成点,其运行的高度y(m)与运行的水平距离x(m)满足关系式y=a(x-6)
2+h.已知球网与O点的水平距离为9 m,高度为2.43 m,球场的边界距O点的水平距离为18 m.
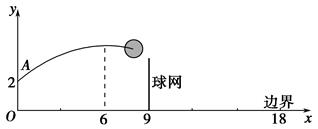
(1)当h=2.6时,求y与x的关系式(不要求写出自变量x的取值范围)
(2)当h=2.6时,球能否越过球网?球会不会出界?请说明理由.
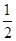 米,在如图所示的坐标系中,这个喷泉的函数关系式是( )
米,在如图所示的坐标系中,这个喷泉的函数关系式是( )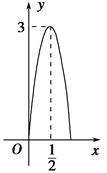
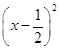 +3
+3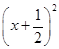 +3
+3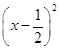 +3
+3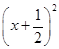 +3
+3

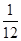 (x-4)2+3,由此可知铅球推出的距离是________m.
(x-4)2+3,由此可知铅球推出的距离是________m.
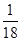 x2+
x2+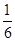 x(0≤x≤10).发射3 s后,导弹到达A点,此时位于与L同一水面的R处雷达站测得AR的距离是2 km,再过3 s后,导弹到达B点.
x(0≤x≤10).发射3 s后,导弹到达A点,此时位于与L同一水面的R处雷达站测得AR的距离是2 km,再过3 s后,导弹到达B点.

