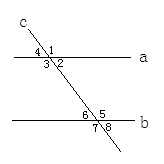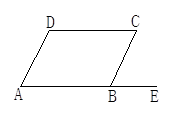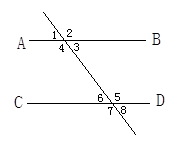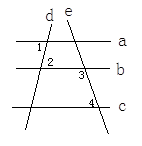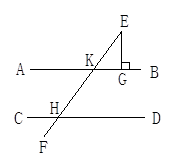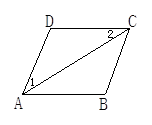适用年级:{{getGradeNameByProperty('初一|同步测试|全国|2012年')}} 试卷类型:{{getTestPaperTypeName('初一|同步测试|全国|2012年')}} 使用省份:{{getAreaName('初一|同步测试|全国|2012年')}}
试卷年份:{{getYear('初一|同步测试|全国|2012年')}}上传日期:2012-10-19题数:13
提示:单击题文可显示答案与解析。
题号:675528
题型:选择题
难易度:较易
日期:2012-10-19
来源:2012年人教版七年级下第五章第二节平行线及其判定(2)练习卷(带解析)
【题文】不相邻的两个直角,如果它们有一边在同一直线上,那么另一边相互( )
| A.平行 | B.垂直 | C.平行或垂直 | D.平行或垂直或相交 |
题号:675529
题型:选择题
难易度:容易
日期:2012-10-19
来源:2012年人教版七年级下第五章第二节平行线及其判定(2)练习卷(带解析)
【题文】下列说法错误的是( )
| A.同位角不一定相等 | B.内错角都相等 |
| C.同旁内角可能相等 | D.同旁内角互补,两直线平行 |
题号:675530
题型:选择题
难易度:较易
日期:2012-10-19
来源:2012年人教版七年级下第五章第二节平行线及其判定(2)练习卷(带解析)
【题文】如图所示,能判断AB∥CE的条件是( )
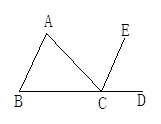
| A.∠A=∠ACE | B.∠A=∠ECD | C.∠B=∠BCA | D.∠B=∠ACE |
题号:675531
题型:选择题
难易度:较易
日期:2012-10-19
来源:2012年人教版七年级下第五章第二节平行线及其判定(2)练习卷(带解析)
【题文】如图所示,如果∠D=∠EFC,那么( )
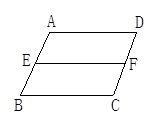
| A.AD∥BC | B.EF∥BC | C.AB∥DC | D.AD∥EF |
题号:675532
题型:选择题
难易度:较易
日期:2012-10-19
来源:2012年人教版七年级下第五章第二节平行线及其判定(2)练习卷(带解析)
【题文】如图所示,下列条件中,能判断AB∥CD的是( )
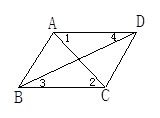
毛
| A.∠BAD=∠BCD | B.∠1=∠2; | C.∠3=∠4 | D.∠BAC=∠ACD |
题号:3943680
题型:选择题
难易度:较易
日期:2012-10-19
来源:2012年人教版七年级下第五章第二节平行线及其判定(2)练习卷(带解析)
【题文】如图所示,直线a,b被直线c所截,现给出下列四个条件:①∠1=∠5;②∠1=∠7;③∠2+∠3=180°;④∠4=∠7.其中能说明a∥b的条件序号为( )
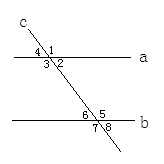
题号:675525
题型:填空题
难易度:较易
日期:2012-10-19
来源:2012年人教版七年级下第五章第二节平行线及其判定(2)练习卷(带解析)
【题文】如图所示,BE是AB的延长线,量得∠CBE=∠A=∠C.
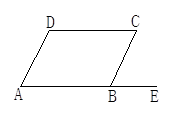
(1)由∠CBE=∠A可以判断______∥______,根据是_________.
(2)由∠CBE=∠C可以判断______∥______,根据是_________.
题号:675526
题型:填空题
难易度:较易
日期:2012-10-19
来源:2012年人教版七年级下第五章第二节平行线及其判定(2)练习卷(带解析)
【题文】在同一平面内,若直线a,b,c满足a⊥b,a⊥c,则b与c的位置关系是______.
题号:675527
题型:填空题
难易度:容易
日期:2012-10-19
来源:2012年人教版七年级下第五章第二节平行线及其判定(2)练习卷(带解析)
【题文】在同一平面内,直线a,b相交于P,若a∥c,则b与c的位置关系是______.
题号:675521
题型:解答题
难易度:较易
日期:2012-10-19
来源:2012年人教版七年级下第五章第二节平行线及其判定(2)练习卷(带解析)
【题文】如图所示,请写出能够得到直线AB∥CD的所有直接条件.
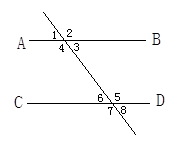
题号:675522
题型:解答题
难易度:较易
日期:2012-10-19
来源:2012年人教版七年级下第五章第二节平行线及其判定(2)练习卷(带解析)
【题文】如图所示,已知直线a,b,c,d,e,且∠1=∠2,∠3+∠4=180°,则a与c平行吗?为什么?
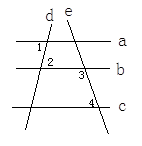
题号:675523
题型:解答题
难易度:较易
日期:2012-10-19
来源:2012年人教版七年级下第五章第二节平行线及其判定(2)练习卷(带解析)
【题文】如图所示,已知直线EF和AB,CD分别相交于K,H,且EG⊥AB,∠CHF=60
0,∠E=30°,试说明AB∥CD.
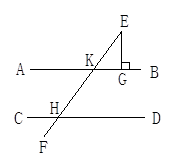
题号:675524
题型:解答题
难易度:容易
日期:2012-10-19
来源:2012年人教版七年级下第五章第二节平行线及其判定(2)练习卷(带解析)
【题文】如图所示,已知∠1=∠2,AC平分∠DAB,试说明DC∥AB.
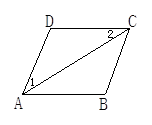
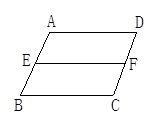
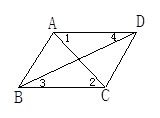 毛
毛