适用年级:{{getGradeNameByProperty('高三|专题试卷|全国|2014年')}} 试卷类型:{{getTestPaperTypeName('高三|专题试卷|全国|2014年')}} 使用省份:{{getAreaName('高三|专题试卷|全国|2014年')}}
试卷年份:{{getYear('高三|专题试卷|全国|2014年')}}上传日期:2014-03-11题数:6
提示:单击题文可显示答案与解析。
题号:950586
题型:解答题
难易度:较难
日期:2014-03-11
来源:2014年高考数学(理)二轮复习体系通关训练2-6练习卷(带解析)
【题文】已知函数
f(
x)=
aln
x-
ax-3(
a∈R).
(1)若
a=-1,求函数
f(
x)的单调区间;
(2)若函数
y=
f(
x)的图象在点(2,
f(2))处的切线的倾斜角为45°,对于任意的
t∈[1,2],函数
g(
x)=
x3+
x2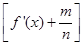
(
f′(
x)是
f(
x)的导函数)在区间(
t,3)上总不是单调函数,求
m的取值范围;
(3)求证:
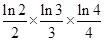
×…×
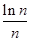
<
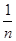
(
n≥2,
n∈N
*)
题号:950587
题型:解答题
难易度:较难
日期:2014-03-11
来源:2014年高考数学(理)二轮复习体系通关训练2-6练习卷(带解析)
【题文】已知向量m=(ex,ln x+k),n=(1,f(x)],m∥n(k为常数),曲线y=f(x)在点(1,f(1))处的切线与y轴垂直,F(x)=xexf′(x).
(1)求k的值及F(x)的单调区间;
(2)已知函数g(x)=-x2+2ax(a为正实数),若对于任意x2∈[0,1],总存在x1∈(0,+∞),使得g(x2)<F(x1),求实数a的取值范围.
题号:950588
题型:解答题
难易度:较难
日期:2014-03-11
来源:2014年高考数学(理)二轮复习体系通关训练2-6练习卷(带解析)
【题文】已知函数
f(
x)=
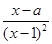
,
x∈(1,+∞).
(1)求函数
f(
x)的单调区间;
(2)函数
f(
x)在区间[2,+∞)上是否存在最小值,若存在,求出最小值,若不存在,请说明理由.
题号:950589
题型:解答题
难易度:困难
日期:2014-03-11
来源:2014年高考数学(理)二轮复习体系通关训练2-6练习卷(带解析)
【题文】已知函数f(x)=axln x图象上点(e,f(e))处的切线与直线y=2x平行,g(x)=x2-tx-2.
(1)求函数f(x)的解析式;
(2)求函数f(x)在[n,n+2](n>0)上的最小值;
(3)对一切x∈(0,e],3f(x)≥g(x)恒成立,求实数t的取值范围.
题号:950590
题型:解答题
难易度:较难
日期:2014-03-11
来源:2014年高考数学(理)二轮复习体系通关训练2-6练习卷(带解析)
【题文】已知函数
f(
x)=
ax+ln
x,
g(
x)=e
x.
(1)当
a≤0时,求
f(
x)的单调区间;
(2)若不等式
g(
x)<
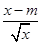
有解,求实数
m的取值范围.
题号:950591
题型:解答题
难易度:较难
日期:2014-03-11
来源:2014年高考数学(理)二轮复习体系通关训练2-6练习卷(带解析)
【题文】已知函数
f(
x)=-
aln
x+
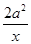
+
x(
a≠0),
(1)若曲线
y=
f(
x)在点(1,
f(1))处的切线与直线
x-2
y=0垂直,求实数
a的值;
(2)讨论函数
f(
x)的单调性.
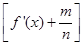 (f′(x)是f(x)的导函数)在区间(t,3)上总不是单调函数,求m的取值范围;
(f′(x)是f(x)的导函数)在区间(t,3)上总不是单调函数,求m的取值范围;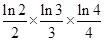 ×…×
×…×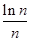 <
<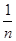 (n≥2,n∈N*)
(n≥2,n∈N*)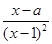 ,x∈(1,+∞).
,x∈(1,+∞).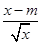 有解,求实数m的取值范围.
有解,求实数m的取值范围.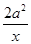 +x(a≠0),
+x(a≠0),