适用年级:{{getGradeNameByProperty('高一|专题试卷|广东|2013年')}} 试卷类型:{{getTestPaperTypeName('高一|专题试卷|广东|2013年')}} 使用省份:{{getAreaName('高一|专题试卷|广东|2013年')}}
试卷年份:{{getYear('高一|专题试卷|广东|2013年')}}上传日期:2013-08-02题数:18
提示:单击题文可显示答案与解析。
题号:982881
题型:选择题
难易度:容易
日期:2013-08-02
来源:2012-2013学年广东省东莞中学高一暑假作业(三)必修2数学试卷(带解析)
【题文】三棱锥
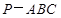
的四个顶点都在体积为
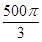
的球的表面上,底面ABC所在的小圆面积为16π,则该三棱锥的高的最大值为( )
题号:982882
题型:选择题
难易度:容易
日期:2013-08-02
来源:2012-2013学年广东省东莞中学高一暑假作业(三)必修2数学试卷(带解析)
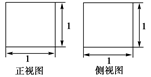
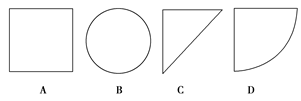
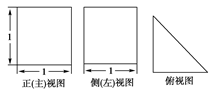
【题文】如图所示,某几何体的正(主)视图与侧(左)视图都是边长为1的正方形,且体积为
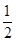
.则该几何体的俯视图可以是( )
题号:982883
题型:选择题
难易度:较易
日期:2013-08-02
来源:2012-2013学年广东省东莞中学高一暑假作业(三)必修2数学试卷(带解析)
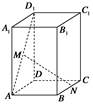
【题文】如图,正四棱柱
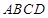
-
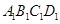
,
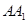
=2,
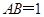
,
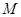
,
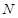
分别在
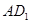
,
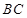
上移动,且始终保持
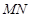
∥平面
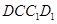
,设
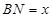
,
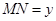
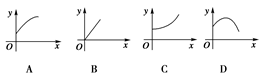
,则函数
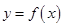
的图象大致是( )
题号:982884
题型:选择题
难易度:容易
日期:2013-08-02
来源:2012-2013学年广东省东莞中学高一暑假作业(三)必修2数学试卷(带解析)
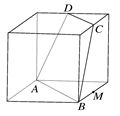
【题文】正方体的棱长为1,
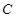
、
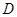
、
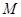
分别为三条棱的中点,
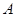
、
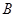
是顶点,那么点
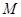
到截面

的距离是( )
题号:982885
题型:选择题
难易度:较易
日期:2013-08-02
来源:2012-2013学年广东省东莞中学高一暑假作业(三)必修2数学试卷(带解析)
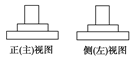
【题文】已知某一几何体的正(主)视图与侧(左)视图如图,则在下列图形中,可以是该几何体的俯视图的图形有( )
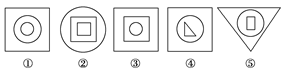
题号:982886
题型:选择题
难易度:较易
日期:2013-08-02
来源:2012-2013学年广东省东莞中学高一暑假作业(三)必修2数学试卷(带解析)
【题文】用一些棱长是1cm的小正方体码放成一个几何体,(1)为其俯视图,(2)为其正(主)视图,则这个几何体的体积最大是( )

题号:982887
题型:选择题
难易度:较易
日期:2013-08-02
来源:2012-2013学年广东省东莞中学高一暑假作业(三)必修2数学试卷(带解析)
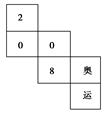
【题文】水平放置的正方体的六个面分别用“前面、后面、上面、下面、左面、右面”表示,如图是一个正方体的表面展开图,若图中“2”在正方体的上面,则这个正方体的下面是( )
题号:982888
题型:选择题
难易度:容易
日期:2013-08-02
来源:2012-2013学年广东省东莞中学高一暑假作业(三)必修2数学试卷(带解析)
【题文】设

、
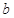
是两条不同的直线,
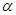
、
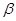
是两个不同的平面,给出下列结论:
①

∥
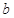
,
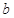
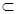
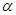
⇒

∥
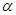
;
②
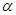
∥
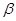
,

∥
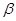
,

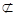
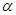
⇒

∥
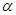
;
③
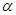
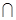
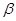
=

,
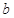
∥
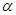
,
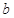
∥
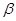
⇒
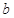
∥

;
④

∥
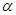
,
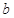
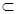
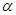
⇒

∥
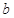
.
其中正确的有( )
题号:982889
题型:选择题
难易度:较易
日期:2013-08-02
来源:2012-2013学年广东省东莞中学高一暑假作业(三)必修2数学试卷(带解析)
【题文】已知一空间几何体的三视图如图所示,它的表面积是( )
题号:3502938
题型:选择题
难易度:容易
日期:2013-08-02
来源:2012-2013学年广东省东莞中学高一暑假作业(三)必修2数学试卷(带解析)
【题文】一个水平放置的平面图形的斜二测直观图是一个底角为45°,腰和上底长均为1的等腰梯形,则这个平面图形的面积是( )
题号:982878
题型:填空题
难易度:容易
日期:2013-08-02
来源:2012-2013学年广东省东莞中学高一暑假作业(三)必修2数学试卷(带解析)
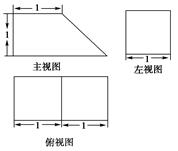
【题文】已知一个几何体的三视图如图所示(单位:cm),其中正(主)视图是直角梯形,侧(左)视图和俯视图都是矩形,则这个几何体的体积是________.
题号:982879
题型:填空题
难易度:较易
日期:2013-08-02
来源:2012-2013学年广东省东莞中学高一暑假作业(三)必修2数学试卷(带解析)
【题文】取棱长为

的正方体的一个顶点,过此顶点出发的三条棱的中点作截面,截去正方体的一个角,对正方体的所有顶点都如此操作,则所剩下的多面体:①有12个顶点 ②有24条棱 ③表面积
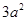
④体积
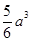
以上结论正确的有________(填上正确的序号).
题号:982880
题型:填空题
难易度:容易
日期:2013-08-02
来源:2012-2013学年广东省东莞中学高一暑假作业(三)必修2数学试卷(带解析)
【题文】一个正方体表面展开图中,五个正方形位置如图阴影所示.第六个正方形在编号1到5的位置,则所有可能位置的编号是_____ _.
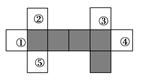
题号:3502939
题型:填空题
难易度:较易
日期:2013-08-02
来源:2012-2013学年广东省东莞中学高一暑假作业(三)必修2数学试卷(带解析)
【题文】如图,已知正三棱柱
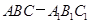
的底面边长为2cm,高为5cm,则一质点自点
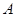
出发,沿着三棱柱的侧面绕行两周到达点
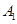
的最短路线的长为________cm.
题号:982876
题型:解答题
难易度:较易
日期:2013-08-02
来源:2012-2013学年广东省东莞中学高一暑假作业(三)必修2数学试卷(带解析)
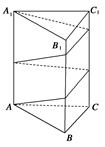
【题文】如图是某直三棱柱(侧棱与底面垂直)被削去上底后的直观图与三视图中的侧(左)视图、俯视图,在直观图中,
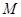
是
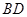
的中点,侧(左)视图是直角梯形,俯视图是等腰直角三角形,有关数据如图所示.
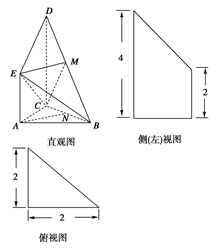
(1)求出该几何体的体积;
(2)若
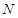
是
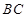
的中点,求证:
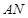
∥平面
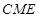
;
(3)求证:平面
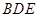
⊥平面
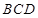
.
题号:982877
题型:解答题
难易度:较易
日期:2013-08-02
来源:2012-2013学年广东省东莞中学高一暑假作业(三)必修2数学试卷(带解析)
【题文】如图,在直角梯形

中,
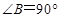
,
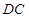
∥
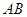
,
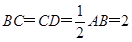
,
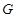
为线段
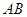
的中点,将
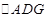
沿
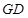
折起,使平面
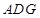
⊥平面
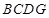
,得到几何体
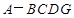
.
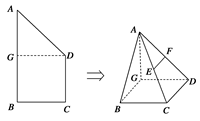
(1)若
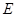
,
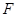
分别为线段
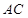
,
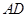
的中点,求证:
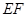
∥平面
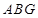
;
(2)求证:
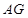
⊥平面
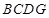
;
(3)
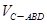
的值.
题号:3502940
题型:解答题
难易度:容易
日期:2013-08-02
来源:2012-2013学年广东省东莞中学高一暑假作业(三)必修2数学试卷(带解析)
【题文】在如图所示的几何体中,四边形

是正方形,
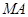
⊥平面

,
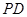
∥
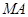
,
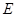
、
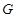
、
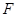
分别为
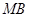
、
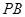
、

的中点,且
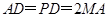
.
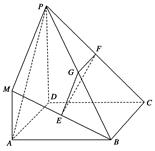
(1)求证:平面
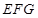
⊥平面
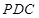
;
(2)求三棱锥
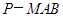
与四棱锥
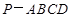
的体积之比.
题号:3502941
题型:解答题
难易度:容易
日期:2013-08-02
来源:2012-2013学年广东省东莞中学高一暑假作业(三)必修2数学试卷(带解析)
【题文】如图所示,矩形

中,
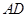
⊥平面
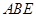
,
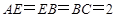
,
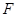
为

上的点,且
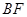
⊥平面

.
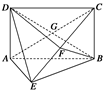
(1)求证:
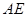
⊥平面

;
(2)求三棱锥
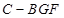
的体积.
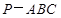 的四个顶点都在体积为
的四个顶点都在体积为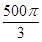 的球的表面上,底面ABC所在的小圆面积为16π,则该三棱锥的高的最大值为( )
的球的表面上,底面ABC所在的小圆面积为16π,则该三棱锥的高的最大值为( )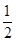 .则该几何体的俯视图可以是( )
.则该几何体的俯视图可以是( )

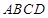 -
-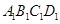 ,
,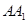 =2,
=2,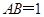 ,
,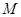 ,
,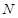 分别在
分别在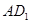 ,
,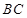 上移动,且始终保持
上移动,且始终保持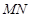 ∥平面
∥平面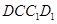 ,设
,设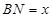 ,
,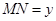 ,则函数
,则函数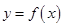 的图象大致是( )
的图象大致是( )

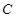 、
、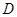 、
、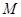 分别为三条棱的中点,
分别为三条棱的中点,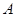 、
、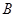 是顶点,那么点
是顶点,那么点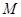 到截面
到截面 的距离是( )
的距离是( )
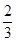
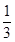
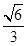
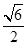



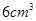
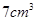
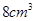
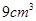

 、
、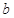 是两条不同的直线,
是两条不同的直线,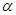 、
、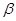 是两个不同的平面,给出下列结论:
是两个不同的平面,给出下列结论: ∥
∥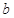 ,
,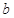
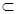
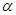 ⇒
⇒ ∥
∥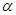 ;
;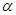 ∥
∥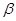 ,
, ∥
∥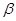 ,
,
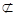
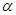 ⇒
⇒ ∥
∥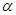 ;
;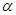
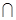
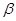 =
= ,
,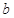 ∥
∥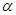 ,
,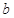 ∥
∥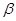 ⇒
⇒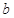 ∥
∥ ;
; ∥
∥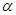 ,
,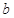
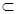
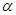 ⇒
⇒ ∥
∥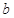 .
. 
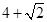
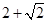
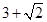
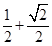
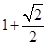
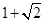
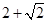

 的正方体的一个顶点,过此顶点出发的三条棱的中点作截面,截去正方体的一个角,对正方体的所有顶点都如此操作,则所剩下的多面体:①有12个顶点 ②有24条棱 ③表面积
的正方体的一个顶点,过此顶点出发的三条棱的中点作截面,截去正方体的一个角,对正方体的所有顶点都如此操作,则所剩下的多面体:①有12个顶点 ②有24条棱 ③表面积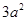 ④体积
④体积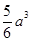

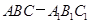 的底面边长为2cm,高为5cm,则一质点自点
的底面边长为2cm,高为5cm,则一质点自点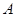 出发,沿着三棱柱的侧面绕行两周到达点
出发,沿着三棱柱的侧面绕行两周到达点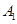 的最短路线的长为________cm.
的最短路线的长为________cm.
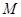 是
是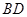 的中点,侧(左)视图是直角梯形,俯视图是等腰直角三角形,有关数据如图所示.
的中点,侧(左)视图是直角梯形,俯视图是等腰直角三角形,有关数据如图所示.
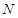 是
是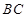 的中点,求证:
的中点,求证: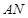 ∥平面
∥平面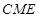 ;
;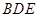 ⊥平面
⊥平面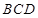 .
. 中,
中,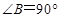 ,
,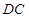 ∥
∥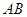 ,
,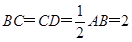 ,
,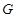 为线段
为线段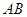 的中点,将
的中点,将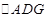 沿
沿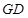 折起,使平面
折起,使平面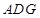 ⊥平面
⊥平面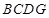 ,得到几何体
,得到几何体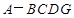 .
.
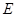 ,
,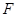 分别为线段
分别为线段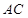 ,
,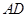 的中点,求证:
的中点,求证: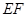 ∥平面
∥平面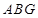 ;
;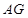 ⊥平面
⊥平面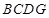 ;
;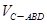 的值.
的值. 是正方形,
是正方形,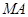 ⊥平面
⊥平面 ,
,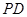 ∥
∥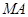 ,
,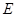 、
、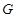 、
、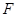 分别为
分别为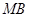 、
、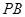 、
、 的中点,且
的中点,且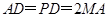 .
.
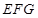 ⊥平面
⊥平面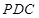 ;
;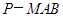 与四棱锥
与四棱锥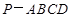 的体积之比.
的体积之比. 中,
中,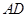 ⊥平面
⊥平面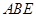 ,
,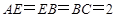 ,
,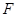 为
为 上的点,且
上的点,且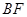 ⊥平面
⊥平面 .
.
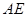 ⊥平面
⊥平面 ;
;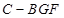 的体积.
的体积.