适用年级:{{getGradeNameByProperty('高三|专题试卷|全国|2014年')}} 试卷类型:{{getTestPaperTypeName('高三|专题试卷|全国|2014年')}} 使用省份:{{getAreaName('高三|专题试卷|全国|2014年')}}
试卷年份:{{getYear('高三|专题试卷|全国|2014年')}}上传日期:2014-03-11题数:6
提示:单击题文可显示答案与解析。
题号:950618
题型:解答题
难易度:较难
日期:2014-03-11
来源:2014年高考数学(理)二轮复习体系通关训练2-4练习卷(带解析)
【题文】在数列{
an}中,
a1=1,{
an}的前
n项和
Sn满足2
Sn=
an+1.
(1)求数列{
an}的通项公式;
(2)若存在
n∈N
*,使得
λ≤
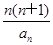
,求实数
λ的最大值.
题号:950619
题型:解答题
难易度:一般
日期:2014-03-11
来源:2014年高考数学(理)二轮复习体系通关训练2-4练习卷(带解析)
【题文】已知{an}为等差数列,且a2=-1,a5=8.
(1)求数列{|an|}的前n项和;
(2)求数列{2n·an}的前n项和.
题号:950620
题型:解答题
难易度:较难
日期:2014-03-11
来源:2014年高考数学(理)二轮复习体系通关训练2-4练习卷(带解析)
【题文】已知数列{
an}的前
n项和
Sn满足
Sn+
an+
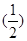 n-1
n-1=2(
n∈N
*),设
cn=2
nan.
(1)求证:数列{
cn}是等差数列,并求数列{
an}的通项公式.
(2)按以下规律构造数列{
bn},具体方法如下:
b1=
c1,
b2=
c2+
c3,
b3=
c4+
c5+
c6+
c7,…,第
n项
bn由相应的{
cn}中2
n-1项的和组成,求数列{
bn}的通项
bn.
题号:950621
题型:解答题
难易度:困难
日期:2014-03-11
来源:2014年高考数学(理)二轮复习体系通关训练2-4练习卷(带解析)
【题文】已知
n∈N
*,数列{
dn}满足
dn=
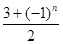
,数列{
an}满足
an=
d1+
d2+
d3+…+
d2n,又知在数列{
bn}中,
b1=2,且对任意正整数
m,
n,
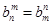
.
(1)求数列{
an}和数列{
bn}的通项公式;
(2)将数列{
bn}中的第
a1项,第
a2项,第
a3项,…,第
an项,…删去后,剩余的项按从小到大的顺序排成新数列{
cn},求数列{
cn}的前2 013项和.
题号:950622
题型:解答题
难易度:较难
日期:2014-03-11
来源:2014年高考数学(理)二轮复习体系通关训练2-4练习卷(带解析)
【题文】已知各项均不相等的等差数列{
an}的前5项和为
S5=35,且
a1+1,
a3+1,
a7+1成等比数列.
(1)求数列{
an}的通项公式;
(2)设
Tn为数列
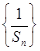
的前
n项和,问是否存在常数
m,使
Tn=
m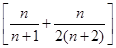
,若存在,求
m的值;若不存在,说明理由.
题号:950623
题型:解答题
难易度:困难
日期:2014-03-11
来源:2014年高考数学(理)二轮复习体系通关训练2-4练习卷(带解析)
【题文】设等比数列{an}的前n项和为Sn,a4=a1-9,a5,a3,a4成等差数列.
(1)求数列{an} 的通项公式;
(2)证明:对任意k∈N*,Sk+2,Sk,Sk+1成等差数列.
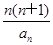 ,求实数λ的最大值.
,求实数λ的最大值.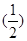 n-1=2(n∈N*),设cn=2nan.
n-1=2(n∈N*),设cn=2nan.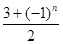 ,数列{an}满足an=d1+d2+d3+…+d2n,又知在数列{bn}中,b1=2,且对任意正整数m,n,
,数列{an}满足an=d1+d2+d3+…+d2n,又知在数列{bn}中,b1=2,且对任意正整数m,n,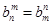 .
.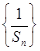 的前n项和,问是否存在常数m,使Tn=m
的前n项和,问是否存在常数m,使Tn=m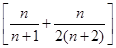 ,若存在,求m的值;若不存在,说明理由.
,若存在,求m的值;若不存在,说明理由.