适用年级:{{getGradeNameByProperty('初三|中考模拟|浙江|2014年')}} 试卷类型:{{getTestPaperTypeName('初三|中考模拟|浙江|2014年')}} 使用省份:{{getAreaName('初三|中考模拟|浙江|2014年')}}
试卷年份:{{getYear('初三|中考模拟|浙江|2014年')}}上传日期:2014-04-29题数:13
提示:单击题文可显示答案与解析。
题号:639156
题型:选择题
难易度:一般
日期:2014-04-29
来源:2014届新人教版初中数学浙江永嘉桥下瓯渠中学中考总复习二十三讲练习卷(带解析)
【题文】在钝角三角形ABC中,AB=AC,点D是BC上一点,AD把△ABC分成两个等腰三角形,则∠BAC的度数为( ).
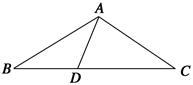
| A.150° | B.124° |
| C.120° | D.108° |
题号:639159
题型:选择题
难易度:较易
日期:2014-04-29
来源:2014届新人教版初中数学浙江永嘉桥下瓯渠中学中考总复习二十三讲练习卷(带解析)
【题文】等腰三角形的两内角度数之比是1∶2,则顶角的度数是 ( )
题号:3562706
题型:选择题
难易度:较易
日期:2014-04-30
来源:2014届新人教版初中数学浙江永嘉桥下瓯渠中学中考总复习二十三讲练习卷(带解析)
【题文】如图,在△ABC中,∠ABC和∠ACB的平分线交于点E,过点E作MN∥BC交AB于M,交AC于N,若BM+CN=9,则线段MN的长为 ( )
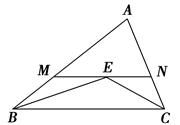
题号:639154
题型:填空题
难易度:较易
日期:2014-04-29
来源:2014届新人教版初中数学浙江永嘉桥下瓯渠中学中考总复习二十三讲练习卷(带解析)
【题文】若等腰三角形的一个外角为70°,则它的底角为________度.
题号:639155
题型:填空题
难易度:较易
日期:2014-04-29
来源:2014届新人教版初中数学浙江永嘉桥下瓯渠中学中考总复习二十三讲练习卷(带解析)
【题文】如图,△ABC中,AB=5,AC=3,BC的垂直平分线交AB于点D,则△ADC的周长为________.
题号:639157
题型:填空题
难易度:较易
日期:2014-04-29
来源:2014届新人教版初中数学浙江永嘉桥下瓯渠中学中考总复习二十三讲练习卷(带解析)
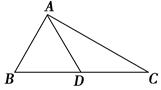
【题文】如图,在△ABC中,AB=AC,BC=6,AD⊥BC于点D,则BD的长是________.
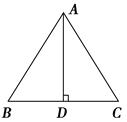
题号:639158
题型:填空题
难易度:较易
日期:2014-04-29
来源:2014届新人教版初中数学浙江永嘉桥下瓯渠中学中考总复习二十三讲练习卷(带解析)
【题文】等腰三角形的两边长分别为6 cm和8 cm,则其周长为________.
题号:3562709
题型:填空题
难易度:一般
日期:2014-04-30
来源:2014届新人教版初中数学浙江永嘉桥下瓯渠中学中考总复习二十三讲练习卷(带解析)
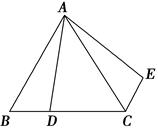
【题文】如图,在等边三角形ABC中,AB=6,D是BC上一点,且BC=3BD,△ABD绕点A旋转后得到△ACE,则CE的长度为________.
题号:3562710
题型:填空题
难易度:较易
日期:2014-04-30
来源:2014届新人教版初中数学浙江永嘉桥下瓯渠中学中考总复习二十三讲练习卷(带解析)
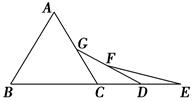
【题文】如图,已知△ABC是等边三角形,点B、C、D、E在同一直线上,且CG=CD,DF=DE,则∠E=________度.
题号:639153
题型:解答题
难易度:一般
日期:2014-04-29
来源:2014届新人教版初中数学浙江永嘉桥下瓯渠中学中考总复习二十三讲练习卷(带解析)
【题文】如图,CD是等边△ABC的角平分线,延长CB到E,使BE=BD,F是AE的中点,已知CD=6 cm,求DF的长.
题号:3562707
题型:解答题
难易度:一般
日期:2014-04-30
来源:2014届新人教版初中数学浙江永嘉桥下瓯渠中学中考总复习二十三讲练习卷(带解析)
【题文】如图,在Rt△ABC中,∠BAC=90°,点D在BC边上,且△ABD是等边三角形,若AB=2,求△ABC的周长.(结果保留根号).
题号:3562708
题型:解答题
难易度:一般
日期:2014-04-30
来源:2014届新人教版初中数学浙江永嘉桥下瓯渠中学中考总复习二十三讲练习卷(带解析)
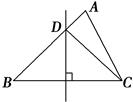
【题文】已知:如图,锐角△ABC的两条高BD、CE相交于点O,且OB=OC,
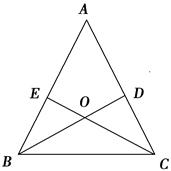
(1)求证:△ABC是等腰三角形;
(2)判断点O是否在∠BAC的角平分线上,并说明理由.
题号:3562711
题型:解答题
难易度:一般
日期:2014-04-30
来源:2014届新人教版初中数学浙江永嘉桥下瓯渠中学中考总复习二十三讲练习卷(带解析)
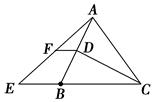
【题文】如图,已知点D为等腰直角△ABC内一点,∠CAD=∠CBD=15°,E为AD延长线上的一点,且CE=CA.
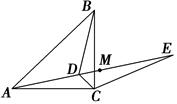
(1)求证:DE平分∠BDC;
(2)若点 M在DE上,且DC=DM,求证:ME=BD.









