适用年级:{{getGradeNameByProperty('初二|同步测试|全国|2017年')}} 试卷类型:{{getTestPaperTypeName('初二|同步测试|全国|2017年')}} 使用省份:{{getAreaName('初二|同步测试|全国|2017年')}}
试卷年份:{{getYear('初二|同步测试|全国|2017年')}}上传日期:2017-11-07题数:12
提示:单击题文可显示答案与解析。
题号:3686747
题型:单选题
难易度:一般
日期:2017-05-23
来源:浙教版八年级数学上册基础训练:2.7 探索勾股定理(一)
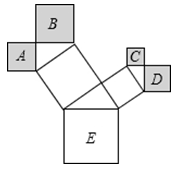
【题文】如图,是一株美丽的勾股树,其中所有的四边形都是正方形,所有的三角形都是直角三角形.若正方形
A、
B、
C、
D的边长分别是3、5、2、3,则最大正方形
E的面积是( )
题号:503536
题型:填空题
难易度:一般
日期:2016-10-12
来源:浙教版八年级数学上册基础训练:2.7 探索勾股定理(一)
【题文】直角三角形斜边长是5,一直角边的长是3,则此直角三角形的面积为___________.
题号:586921
题型:填空题
难易度:较易
日期:2015-09-22
来源:浙教版八年级数学上册基础训练:2.7 探索勾股定理(一)
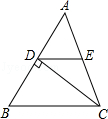
【题文】如图,△ABC中,CD⊥AB于D,E是AC的中点.若AD=6,DE=5,则CD的长等于
.
题号:595004
题型:填空题
难易度:一般
日期:2015-07-20
来源:浙教版八年级数学上册基础训练:2.7 探索勾股定理(一)
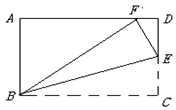
【题文】如图,在矩形ABCD中,AB=3,BC=5,在CD上任取一点E,连接BE,将△BCE沿BE折叠,使点E恰好落在AD边上的点F处,则CE的长为
.
题号:620626
题型:填空题
难易度:一般
日期:2015-02-06
来源:浙教版八年级数学上册基础训练:2.7 探索勾股定理(一)
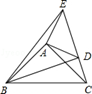
【题文】已知:如图在△ABC,△ADE中,∠BAC=∠DAE=90°,AB=AC,AD=AE,点C,D,E三点同一条直线上,连接BD,BE.以下四个结论:
①BD=CE;②BD⊥CE;③∠ACE+∠DBC=45°;④BE
2=2(AD
2+AB
2).
错误的结论有
(填序号).
题号:631183
题型:填空题
难易度:一般
日期:2014-11-05
来源:浙教版八年级数学上册基础训练:2.7 探索勾股定理(一)
【题文】
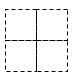
如图是由4个边长为1的正方形构成的“田字格”.只用没有刻度的直尺在这个“田字格”中最多可以作出长度为
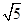
的线段__________条.
题号:631238
题型:填空题
难易度:一般
日期:2014-11-04
来源:浙教版八年级数学上册基础训练:2.7 探索勾股定理(一)
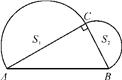
【题文】如图,已知在Rt△ABC中,∠ACB=90°,AB=4,分别以AC,BC为直径作半圆,面积分别记为S
1,S
2,则S
1+S
2等于____________.
题号:597603
题型:解答题
难易度:一般
日期:2015-07-06
来源:浙教版八年级数学上册基础训练:2.7 探索勾股定理(一)
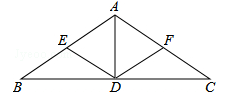
【题文】(本题满分7分)如图,在△ABC中,AB=AC,点E,F分别是边AB,AC的中点,点D在边BC上.若DE=DF,AD=2,BC=6,求四边形AEDF的周长.
题号:5953452
题型:解答题
难易度:一般
日期:2017-11-06
来源:浙教版八年级数学上册基础训练:2.7 探索勾股定理(一)
【题文】在△ABC中,∠C=90°,BC=a,AC=b,AB=c.
(1)若a=5,b=12,求c.
(2)若b=0.7,c=2.5,求a.
(3)若a∶b=3∶4,c=25,求b.
题号:5953453
题型:解答题
难易度:一般
日期:2017-11-06
来源:浙教版八年级数学上册基础训练:2.7 探索勾股定理(一)
【题文】在△ABC中,AB=13 cm,AC=20 cm,BC边上的高为12 cm,求△ABC的面积.
题号:5953454
题型:解答题
难易度:较难
日期:2017-11-06
来源:浙教版八年级数学上册基础训练:2.7 探索勾股定理(一)
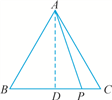
【题文】如图,在△
ABC中,
AB=
AC=4,
P为
BC边上任意一点.
(1)求证:
AP2+
PB·
PC=16.
(2)若
BC边上有100个不同的点(不与点
B,
C重合)
P1,
P2,…,
P100,设
mi=
APi2+
PiB·
PiC(
i=1,2,…,100).求
m1+
m2+…+
m100的值.
题号:5953455
题型:解答题
难易度:一般
日期:2017-11-06
来源:浙教版八年级数学上册基础训练:2.7 探索勾股定理(一)
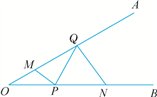
【题文】如图,∠
AOB=30°,点
M,
N分别在边
OA,
OB上,且
OM=1,
ON=3,点
P,
Q分别在边
OB,
OA上,求
MP+
PQ+
QN的最小值.




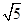 的线段__________条.
的线段__________条.



