适用年级:{{getGradeNameByProperty('高三|专题试卷|全国|2014年')}} 试卷类型:{{getTestPaperTypeName('高三|专题试卷|全国|2014年')}} 使用省份:{{getAreaName('高三|专题试卷|全国|2014年')}}
试卷年份:{{getYear('高三|专题试卷|全国|2014年')}}上传日期:2014-04-15题数:19
提示:单击题文可显示答案与解析。
题号:934898
题型:解答题
难易度:一般
日期:2014-04-15
来源:2014届人教版高考数学文科二轮专题复习提分训练26练习卷(带解析)
【题文】如图所示,在底面为直角梯形的四棱锥P

ABCD中,AD∥BC,PD⊥平面ABCD,AD=1,AB=
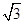
,BC=4.
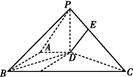
(1)求证:BD⊥PC;
(2)求直线AB与平面PDC所成的角;
(3)设点E在棱PC上,
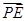
=λ
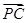
,若DE∥平面PAB,求λ的值.
题号:934899
题型:解答题
难易度:一般
日期:2014-04-15
来源:2014届人教版高考数学文科二轮专题复习提分训练26练习卷(带解析)
【题文】如图所示,四棱锥P

ABCD的底面为正方形,侧棱PA⊥底面ABCD,且PA=AD=2,E,F,H分别是线段PA,PD,AB的中点.
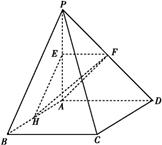
(1)求证:PB∥平面EFH;
(2)求证:PD⊥平面AHF.
题号:934900
题型:解答题
难易度:较难
日期:2014-04-15
来源:2014届人教版高考数学文科二轮专题复习提分训练26练习卷(带解析)
【题文】如图所示,已知三棱柱ABC

A
1B
1C
1,
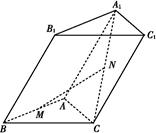
(1)若M、N分别是AB,A
1C的中点,求证:MN∥平面BCC
1B
1;
(2)若三棱柱ABC

A
1B
1C
1的各棱长均为2,∠B
1BA=∠B
1BC=60°,P为线段B
1B上的动点,当PA+PC最小时,求证:B
1B⊥平面APC.
题号:934901
题型:解答题
难易度:一般
日期:2014-04-15
来源:2014届人教版高考数学文科二轮专题复习提分训练26练习卷(带解析)
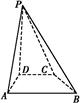
【题文】如图所示,四边形ABCD中,AB⊥AD,AD∥BC,AD=6,BC=4,AB=2,点E、F分别在BC、AD上,EF∥AB.现将四边形ABEF沿EF折起,使平面ABEF⊥平面EFDC,设AD中点为P.
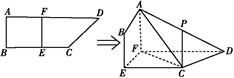
(1)当E为BC中点时,求证:CP∥平面ABEF;
(2)设BE=x,问当x为何值时,三棱锥A

CDF的体积有最大值?并求出这个最大值.
题号:934902
题型:解答题
难易度:较难
日期:2014-04-15
来源:2014届人教版高考数学文科二轮专题复习提分训练26练习卷(带解析)
【题文】一个多面体的直观图和三视图如图所示,其中M,N分别是AB,AC的中点,G是DF上的一动点.
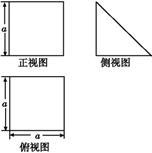
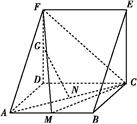
(1)求该多面体的体积与表面积;
(2)求证:GN⊥AC;
(3)当FG=GD时,在棱AD上确定一点P,使得GP∥平面FMC,并给出证明.
题号:934903
题型:解答题
难易度:一般
日期:2014-04-15
来源:2014届人教版高考数学文科二轮专题复习提分训练26练习卷(带解析)
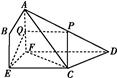
【题文】如图所示,四棱锥E

ABCD中,EA=EB,AB∥CD,AB⊥BC,AB=2CD.
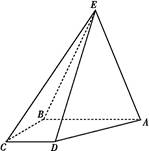
(1)求证:AB⊥ED;
(2)线段EA上是否存在点F,使DF∥平面BCE?若存在,求出
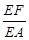
;若不存在,说明理由.
题号:934904
题型:解答题
难易度:一般
日期:2014-04-15
来源:2014届人教版高考数学文科二轮专题复习提分训练26练习卷(带解析)
【题文】如图,在四面体PABC中,PC⊥AB,PA⊥BC,点D,E,F,G分别是棱AP,AC,BC,PB的中点.
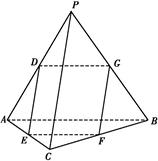
(1)求证:DE∥平面BCP.
(2)求证:四边形DEFG为矩形.
(3)是否存在点Q,到四面体PABC六条棱的中点的距离相等?说明理由.
题号:934905
题型:解答题
难易度:困难
日期:2014-04-15
来源:2014届人教版高考数学文科二轮专题复习提分训练26练习卷(带解析)
【题文】如图,在平行四边形ABCD中,AB=2BC,∠ABC=120°,E为线段AB的中点,将△ADE沿直线DE翻折成△A′DE,使平面A′DE⊥平面BCD,F为线段A′C的中点.
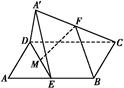
(1)求证:BF∥平面A′DE;
(2)设M为线段DE的中点,求直线FM与平面A′DE所成角的余弦值.
题号:934906
题型:解答题
难易度:一般
日期:2014-04-15
来源:2014届人教版高考数学文科二轮专题复习提分训练26练习卷(带解析)
【题文】如图,正方形ABCD和四边形ACEF所在的平面互相垂直,EF∥AC,AB=
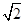
,CE=EF=1.
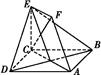
(1)求证:AF∥平面BDE;
(2)求证:CF⊥平面BDE.
题号:934907
题型:解答题
难易度:较难
日期:2014-04-15
来源:2014届人教版高考数学文科二轮专题复习提分训练26练习卷(带解析)
【题文】如图,在四棱锥P

ABCD中,底面是边长为2
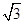
的菱形,∠BAD=120°,且PA⊥平面ABCD,PA=2
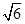
,M、N分别为PB、PD的中点.
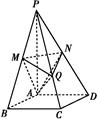
(1)证明:MN∥平面ABCD;
(2)过点A作AQ⊥PC,垂足为点Q,求二面角A

MN

Q的平面角的余弦值.
题号:934908
题型:解答题
难易度:一般
日期:2014-04-15
来源:2014届人教版高考数学文科二轮专题复习提分训练26练习卷(带解析)
【题文】如图,四棱锥P

ABCD中,AB⊥AC,AB⊥PA,AB∥CD,AB=2CD,E,F,G,M,N分别为PB,AB,BC,PD,PC的中点
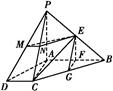
(1)求证:CE∥平面PAD;
(2)求证:平面EFG⊥平面EMN.
题号:934909
题型:解答题
难易度:较难
日期:2014-04-15
来源:2014届人教版高考数学文科二轮专题复习提分训练26练习卷(带解析)
【题文】如图,在四棱锥P

ABCD中,PD⊥平面ABCD,AB∥DC,AB⊥AD,BC=5,DC=3,AD=4,∠PAD=60°.
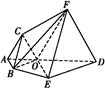
(1)当正视方向与向量
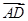
的方向相同时,画出四棱锥P

ABCD的正视图(要求标出尺寸,并写出演算过程);
(2)若M为PA的中点,求证:DM∥平面PBC;
(3)求三棱锥D

PBC的体积.
题号:934910
题型:解答题
难易度:较难
日期:2014-04-15
来源:2014届人教版高考数学文科二轮专题复习提分训练26练习卷(带解析)
【题文】如图,ABEDFC为多面体,平面ABED与平面ACFD垂直,点O在线段AD上,OA=1,OD=2,△OAB,△OAC,△ODE,△ODF都是正三角形.
(1)证明直线BC∥EF;
(2)求棱锥F

OBED的体积.
题号:934911
题型:解答题
难易度:较难
日期:2014-04-15
来源:2014届人教版高考数学文科二轮专题复习提分训练26练习卷(带解析)
【题文】如图,在侧棱垂直底面的四棱柱ABCD

A
1B
1C
1D
1中,AD∥BC,AD⊥AB,AB=
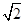
,AD=2,BC=4,AA
1=2,E是DD
1的中点,F是平面B
1C
1E与直线AA
1的交点.
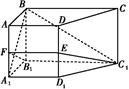
(1)证明:①EF∥A
1D
1;②BA
1⊥平面B
1C
1EF.
(2)求BC
1与平面B
1C
1EF所成的角的正弦值.
题号:3485419
题型:解答题
难易度:一般
日期:2014-04-17
来源:2014届人教版高考数学文科二轮专题复习提分训练26练习卷(带解析)
【题文】如图,在三棱锥S

ABC中,平面SAB⊥平面SBC,AB⊥BC,AS=AB.过A作AF⊥SB,垂足为F,点E,G分别是棱SA,SC的中点.
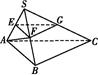
求证:(1)平面EFG∥平面ABC;
(2)BC⊥SA.
题号:3485420
题型:解答题
难易度:较难
日期:2014-04-17
来源:2014届人教版高考数学文科二轮专题复习提分训练26练习卷(带解析)
【题文】如图,直三棱柱ABC

A′B′C′,∠BAC=90°,AB=AC=
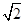
,AA′=1,点M,N分别为
A′B和B′C′的中点.
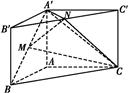
(1)证明:MN∥平面A′ACC′;
(2)求三棱锥A′

MNC的体积.(锥体体积公式V=
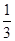
Sh,其中S为底面面积,h为高)
题号:3485421
题型:解答题
难易度:一般
日期:2014-04-17
来源:2014届人教版高考数学文科二轮专题复习提分训练26练习卷(带解析)
【题文】如图,几何体E

ABCD是四棱锥,△ABD为正三角形,CB=CD,EC⊥BD.
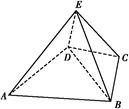
(1)求证:BE=DE;
(2)若∠BCD=120°,M为线段AE的中点,求证:DM∥平面BEC.
题号:3485422
题型:解答题
难易度:较难
日期:2014-04-17
来源:2014届人教版高考数学文科二轮专题复习提分训练26练习卷(带解析)
【题文】如图,四棱锥S

ABCD的底面是正方形,每条侧棱的长都是底面边长的
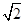
倍,P为侧棱SD上的点.
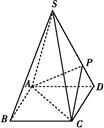
(1)求证:AC⊥SD;
(2)若SD⊥平面PAC,求二面角P

AC

D的大小;
(3)在(2)的条件下,侧棱SC上是否存在一点E,使得BE∥平面PAC.若存在,求SE∶EC的值;若不存在,试说明理由.
题号:3485423
题型:解答题
难易度:一般
日期:2014-04-17
来源:2014届人教版高考数学文科二轮专题复习提分训练26练习卷(带解析)
【题文】如图五面体中,四边形ABCD是矩形,DA⊥平面ABEF,AB∥EF,AB=
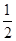
EF=2
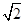
,AF=BE=2,P、Q、M分别为AE、BD、EF的中点.
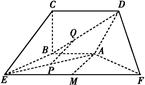
(1)求证:PQ∥平面BCE;
(2)求证:AM⊥平面ADF.
 ABCD中,AD∥BC,PD⊥平面ABCD,AD=1,AB=
ABCD中,AD∥BC,PD⊥平面ABCD,AD=1,AB=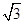 ,BC=4.
,BC=4.
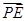 =λ
=λ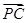 ,若DE∥平面PAB,求λ的值.
,若DE∥平面PAB,求λ的值. ABCD的底面为正方形,侧棱PA⊥底面ABCD,且PA=AD=2,E,F,H分别是线段PA,PD,AB的中点.
ABCD的底面为正方形,侧棱PA⊥底面ABCD,且PA=AD=2,E,F,H分别是线段PA,PD,AB的中点.
 A1B1C1,
A1B1C1,
 A1B1C1的各棱长均为2,∠B1BA=∠B1BC=60°,P为线段B1B上的动点,当PA+PC最小时,求证:B1B⊥平面APC.
A1B1C1的各棱长均为2,∠B1BA=∠B1BC=60°,P为线段B1B上的动点,当PA+PC最小时,求证:B1B⊥平面APC.
 CDF的体积有最大值?并求出这个最大值.
CDF的体积有最大值?并求出这个最大值.


 ABCD中,EA=EB,AB∥CD,AB⊥BC,AB=2CD.
ABCD中,EA=EB,AB∥CD,AB⊥BC,AB=2CD.
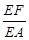 ;若不存在,说明理由.
;若不存在,说明理由.

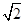 ,CE=EF=1.
,CE=EF=1.
 ABCD中,底面是边长为2
ABCD中,底面是边长为2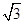 的菱形,∠BAD=120°,且PA⊥平面ABCD,PA=2
的菱形,∠BAD=120°,且PA⊥平面ABCD,PA=2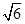 ,M、N分别为PB、PD的中点.
,M、N分别为PB、PD的中点.
 MN
MN Q的平面角的余弦值.
Q的平面角的余弦值. ABCD中,AB⊥AC,AB⊥PA,AB∥CD,AB=2CD,E,F,G,M,N分别为PB,AB,BC,PD,PC的中点
ABCD中,AB⊥AC,AB⊥PA,AB∥CD,AB=2CD,E,F,G,M,N分别为PB,AB,BC,PD,PC的中点
 ABCD中,PD⊥平面ABCD,AB∥DC,AB⊥AD,BC=5,DC=3,AD=4,∠PAD=60°.
ABCD中,PD⊥平面ABCD,AB∥DC,AB⊥AD,BC=5,DC=3,AD=4,∠PAD=60°.
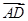 的方向相同时,画出四棱锥P
的方向相同时,画出四棱锥P ABCD的正视图(要求标出尺寸,并写出演算过程);
ABCD的正视图(要求标出尺寸,并写出演算过程); PBC的体积.
PBC的体积.
 OBED的体积.
OBED的体积. A1B1C1D1中,AD∥BC,AD⊥AB,AB=
A1B1C1D1中,AD∥BC,AD⊥AB,AB=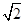 ,AD=2,BC=4,AA1=2,E是DD1的中点,F是平面B1C1E与直线AA1的交点.
,AD=2,BC=4,AA1=2,E是DD1的中点,F是平面B1C1E与直线AA1的交点.
 ABC中,平面SAB⊥平面SBC,AB⊥BC,AS=AB.过A作AF⊥SB,垂足为F,点E,G分别是棱SA,SC的中点.
ABC中,平面SAB⊥平面SBC,AB⊥BC,AS=AB.过A作AF⊥SB,垂足为F,点E,G分别是棱SA,SC的中点.
 A′B′C′,∠BAC=90°,AB=AC=
A′B′C′,∠BAC=90°,AB=AC=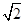 ,AA′=1,点M,N分别为
,AA′=1,点M,N分别为
 MNC的体积.(锥体体积公式V=
MNC的体积.(锥体体积公式V=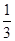 Sh,其中S为底面面积,h为高)
Sh,其中S为底面面积,h为高) ABCD是四棱锥,△ABD为正三角形,CB=CD,EC⊥BD.
ABCD是四棱锥,△ABD为正三角形,CB=CD,EC⊥BD.
 ABCD的底面是正方形,每条侧棱的长都是底面边长的
ABCD的底面是正方形,每条侧棱的长都是底面边长的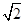 倍,P为侧棱SD上的点.
倍,P为侧棱SD上的点.
 AC
AC D的大小;
D的大小;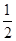 EF=2
EF=2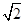 ,AF=BE=2,P、Q、M分别为AE、BD、EF的中点.
,AF=BE=2,P、Q、M分别为AE、BD、EF的中点.