适用年级:{{getGradeNameByProperty('高三|专题试卷|全国|2014年')}} 试卷类型:{{getTestPaperTypeName('高三|专题试卷|全国|2014年')}} 使用省份:{{getAreaName('高三|专题试卷|全国|2014年')}}
试卷年份:{{getYear('高三|专题试卷|全国|2014年')}}上传日期:2014-04-11题数:15
提示:单击题文可显示答案与解析。
题号:936811
题型:填空题
难易度:一般
日期:2014-04-11
来源:2014届高考数学总复习考点引领+技巧点拨第五章第1课时练习卷(带解析)
【题文】若an=n2+λn+3(其中λ为实常数),n∈N*,且数列{an}为单调递增数列,则实数λ的取值范围为________.
题号:936852
题型:填空题
难易度:较易
日期:2014-04-11
来源:2014届高考数学总复习考点引领+技巧点拨第五章第1课时练习卷(带解析)
【题文】若数列
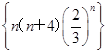
中的最大项是第k项,则k=________.
题号:936853
题型:填空题
难易度:一般
日期:2014-04-11
来源:2014届高考数学总复习考点引领+技巧点拨第五章第1课时练习卷(带解析)
【题文】设S
n为数列{a
n}的前n项和,若S
n=(-1)
na
n-
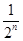
,n∈N
,则a
3=________.
题号:936854
题型:填空题
难易度:较易
日期:2014-04-11
来源:2014届高考数学总复习考点引领+技巧点拨第五章第1课时练习卷(带解析)
【题文】已知数列{an}的前n项和为Sn,满足log2(1+Sn)=n+1,则{an}的通项公式为__________.
题号:936855
题型:填空题
难易度:较易
日期:2014-04-11
来源:2014届高考数学总复习考点引领+技巧点拨第五章第1课时练习卷(带解析)
【题文】设a>0,若a
n=
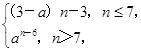
且数列{a
n}是递增数列,则实数a的范围是__________.
题号:936856
题型:填空题
难易度:较易
日期:2014-04-11
来源:2014届高考数学总复习考点引领+技巧点拨第五章第1课时练习卷(带解析)
【题文】已知a1=1,an=n(an+1-an)(n∈N*),则数列{an}的通项公式是________.
题号:936861
题型:填空题
难易度:一般
日期:2014-04-11
来源:2014届高考数学总复习考点引领+技巧点拨第五章第1课时练习卷(带解析)
【题文】已知数列{an}的通项公式是an=n2-8n+5,这个数列的最小项是________.
题号:936862
题型:填空题
难易度:容易
日期:2014-04-11
来源:2014届高考数学总复习考点引领+技巧点拨第五章第1课时练习卷(带解析)
【题文】若数列{an}的前n项和Sn=n2+3n,则a6+a7+a8=________.
题号:698197
题型:解答题
难易度:一般
日期:2016-11-10
来源:2014届高考数学总复习考点引领+技巧点拨第五章第1课时练习卷(带解析)
【题文】已知函数f(x)=ax2+bx(a≠0)的导函数f′(x)=-2x+7,数列{an}的前n项和为Sn,点Pn(n,Sn)(n∈N*)均在函数y=f(x)的图象上,求数列{an}的通项公式及Sn的最大值.
题号:936808
题型:解答题
难易度:较难
日期:2014-04-11
来源:2014届高考数学总复习考点引领+技巧点拨第五章第1课时练习卷(带解析)
【题文】已知数列的前n项和为S
n,并且满足a
1=2,na
n+1=S
n+n(n+1).
(1)求{a
n}的通项公式;
(2)令T
n=
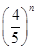
S
n,是否存在正整数m,对一切正整数n,总有T
n≤T
m?若存在,求m的值;若不存在,说明理由.
题号:936809
题型:解答题
难易度:较难
日期:2014-04-11
来源:2014届高考数学总复习考点引领+技巧点拨第五章第1课时练习卷(带解析)
【题文】若数列{an}满足an+1=an+an+2(n∈N*),则称数列{an}为“凸数列”.
(1)设数列{an}为“凸数列”,若a1=1,a2=-2,试写出该数列的前6项,并求出前6项之和;
(2)在“凸数列”{an}中,求证:an+3=-an,n∈N*;
(3)设a1=a,a2=b,若数列{an}为“凸数列”,求数列前2011项和S2011.
题号:936810
题型:解答题
难易度:较难
日期:2014-04-11
来源:2014届高考数学总复习考点引领+技巧点拨第五章第1课时练习卷(带解析)
【题文】已知an=n×0.8n(n∈N*).
(1)判断数列{an}的单调性;
(2)是否存在最小正整数k,使得数列{an}中的任意一项均小于k?请说明理由.
题号:936857
题型:解答题
难易度:较难
日期:2014-04-11
来源:2014届高考数学总复习考点引领+技巧点拨第五章第1课时练习卷(带解析)
【题文】已知数列
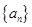
的通项公式a
n=
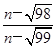
(n∈N
*),求数列前30项中的最大项和最小项.
题号:936858
题型:解答题
难易度:较易
日期:2014-04-11
来源:2014届高考数学总复习考点引领+技巧点拨第五章第1课时练习卷(带解析)
【题文】如下表定义函数f(x):
对于数列{a
n},a
1=4,a
n=f(a
n-1),n=2,3,4,…,求a
2008.
题号:936860
题型:解答题
难易度:一般
日期:2014-04-11
来源:2014届高考数学总复习考点引领+技巧点拨第五章第1课时练习卷(带解析)
【题文】已知数列{an}的前n项和Sn,求通项an.
(1)Sn=3n-1;
(2)Sn=n2+3n+1.
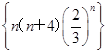 中的最大项是第k项,则k=________.
中的最大项是第k项,则k=________.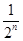 ,n∈N,则a3=________.
,n∈N,则a3=________.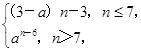 且数列{an}是递增数列,则实数a的范围是__________.
且数列{an}是递增数列,则实数a的范围是__________.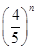 Sn,是否存在正整数m,对一切正整数n,总有Tn≤Tm?若存在,求m的值;若不存在,说明理由.
Sn,是否存在正整数m,对一切正整数n,总有Tn≤Tm?若存在,求m的值;若不存在,说明理由.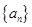 的通项公式an=
的通项公式an=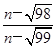 (n∈N*),求数列前30项中的最大项和最小项.
(n∈N*),求数列前30项中的最大项和最小项.