适用年级:{{getGradeNameByProperty('高三|专题试卷|全国|2014年')}} 试卷类型:{{getTestPaperTypeName('高三|专题试卷|全国|2014年')}} 使用省份:{{getAreaName('高三|专题试卷|全国|2014年')}}
试卷年份:{{getYear('高三|专题试卷|全国|2014年')}}上传日期:2014-03-18题数:5
提示:单击题文可显示答案与解析。
题号:948019
题型:解答题
难易度:较难
日期:2014-03-18
来源:2014届高考数学(文)三轮专题体系通关训练倒数第2天练习卷(带解析)
【题文】已知数列{
an}满足:
a1=
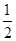
,
an+1=
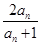
(
n∈N
*).
(1)求
a2,
a3的值;
(2)证明:不等式0<
an<
an+1对于任意
n∈N
*都成立.
题号:948020
题型:解答题
难易度:较难
日期:2014-03-18
来源:2014届高考数学(文)三轮专题体系通关训练倒数第2天练习卷(带解析)
【题文】设m,n∈N*,f(x)=(1+2x)m+(1+x)n.
(1)当m=n=2 011时,记f(x)=a0+a1x+a2x2+…+a2 011x2 011,求a0-a1+a2-…-a2 011;
(2)若f(x)展开式中x的系数是20,则当m,n变化时,试求x2系数的最小值.
题号:948021
题型:解答题
难易度:较难
日期:2014-03-18
来源:2014届高考数学(文)三轮专题体系通关训练倒数第2天练习卷(带解析)
【题文】某校高一、高二两个年级进行乒乓球对抗赛,每个年级选出3名学生组成代表队,比赛规则是:①按“单打、双打、单打”顺序进行三盘比赛;②代表队中每名队员至少参加一盘比赛,但不能参加两盘单打比赛.若每盘比赛中高一、高二获胜的概率分别为
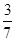
,

.
(1)按比赛规则,高一年级代表队可以派出多少种不同的出场阵容?
(2)若单打获胜得2分,双打获胜得3分,求高一年级得分
ξ的概率分布列和数学期望.
题号:948022
题型:解答题
难易度:较难
日期:2014-03-18
来源:2014届高考数学(文)三轮专题体系通关训练倒数第2天练习卷(带解析)
【题文】如图,在长方体
ABCD
A1B1C1D1中,已知
AB=4,
AD=3,
AA1=2,
E,
F分别是棱
AB,
BC上的点,且
EB=
FB=1.

(1)求异面直线
EC1与
FD1所成角的余弦值;
(2)试在面
A1B1C1D1上确定一点
G,使
DG⊥平面
D1EF.
题号:948023
题型:解答题
难易度:较难
日期:2014-03-18
来源:2014届高考数学(文)三轮专题体系通关训练倒数第2天练习卷(带解析)
【题文】如图,在直三棱柱
ABC
A1B1C1中,∠
ACB=90°,∠
BAC=30°,
BC=1,
A1A=
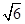
,
M是
CC1的中点.

(1)求证:
A1B⊥
AM;
(2)求二面角
B
AM
C的平面角的大小..
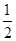 ,an+1=
,an+1=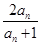 (n∈N*).
(n∈N*).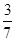 ,
, .
.
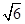 ,M是CC1的中点.
,M是CC1的中点.