适用年级:{{getGradeNameByProperty('高三|专题试卷|全国|2014年')}} 试卷类型:{{getTestPaperTypeName('高三|专题试卷|全国|2014年')}} 使用省份:{{getAreaName('高三|专题试卷|全国|2014年')}}
试卷年份:{{getYear('高三|专题试卷|全国|2014年')}}上传日期:2014-03-17题数:11
提示:单击题文可显示答案与解析。
题号:948328
题型:选择题
难易度:容易
日期:2014-03-17
来源:2014年高考数学(理)二轮专题复习知能提升演练选修4-4练习卷(带解析)
【题文】已知椭圆的参数方程
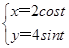
(
t为参数),点
M在椭圆上,对应参数
t=
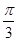
,点
O为原点,则直线
OM的斜率为 ( ).
题号:948329
题型:选择题
难易度:容易
日期:2014-03-17
来源:2014年高考数学(理)二轮专题复习知能提升演练选修4-4练习卷(带解析)
【题文】极坐标方程
ρ=cos
θ和参数方程
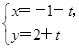
(
t为参数)所表示的图形分别是( ).
题号:4187688
题型:选择题
难易度:容易
日期:2014-03-21
来源:2014年高考数学(理)二轮专题复习知能提升演练选修4-4练习卷(带解析)
【题文】在极坐标系中,圆
ρ=2cos
θ的垂直于极轴的两条切线方程分别为( ).
| A.θ=0(ρ∈R)和ρcosθ=2 | B.θ=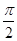 (ρ∈R)和ρcos θ=2 (ρ∈R)和ρcos θ=2 |
C.θ=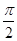 (ρ∈R)和ρcos θ=1 (ρ∈R)和ρcos θ=1 | D.θ=0(ρ∈R)和ρcos θ=1 |
题号:948324
题型:填空题
难易度:一般
日期:2014-03-17
来源:2014年高考数学(理)二轮专题复习知能提升演练选修4-4练习卷(带解析)
【题文】在直角坐标系
xOy中,以原点
O为极点,
x轴的正半轴为极轴建立极坐标系.已知射线
θ=
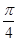
与曲线
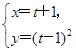
(
t为参数)相交于
A,
B两点,则线段
AB的中点的直角坐标为________.
题号:948325
题型:填空题
难易度:一般
日期:2014-03-17
来源:2014年高考数学(理)二轮专题复习知能提升演练选修4-4练习卷(带解析)
【题文】已知曲线C的极坐标方程为ρ=2cos θ,以极点为原点,极轴为x轴的正半轴建立直角坐标系,则曲线C的参数方程为________.
题号:948326
题型:填空题
难易度:一般
日期:2014-03-17
来源:2014年高考数学(理)二轮专题复习知能提升演练选修4-4练习卷(带解析)
【题文】设曲线
C的参数方程为
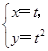
(
t为参数),若以直角坐标系的原点为极点,
x轴的正半轴为极轴建立极坐标系,则曲线
C的极坐标方程为________.
题号:948327
题型:填空题
难易度:一般
日期:2014-03-17
来源:2014年高考数学(理)二轮专题复习知能提升演练选修4-4练习卷(带解析)
【题文】直线
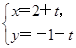
(
t为参数)与曲线
C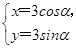
(
α为参数)的交点个数为________.
题号:4187689
题型:填空题
难易度:一般
日期:2014-03-21
来源:2014年高考数学(理)二轮专题复习知能提升演练选修4-4练习卷(带解析)
【题文】在极坐标系中,点
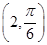
到直线
ρsin
θ=2的距离等于________.
题号:948323
题型:解答题
难易度:一般
日期:2014-03-17
来源:2014年高考数学(理)二轮专题复习知能提升演练选修4-4练习卷(带解析)
【题文】已知曲线
C1的参数方程是
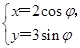
(
φ为参数),以坐标原点为极点,
x轴的正半轴为极轴建立极坐标系,曲线
C2的极坐标方程是
ρ=2.正方形
ABCD的顶点都在
C2上,且
A,
B,
C,
D依逆时针次序排列,点
A的极坐标为
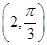
.
(1)求点
A,
B,
C,
D的直角坐标;
(2)设
P为
C1上任意一点,求|
PA|
2+|
PB|
2+|
PC|
2+|
PD|
2的取值范围.
题号:4187690
题型:解答题
难易度:一般
日期:2014-03-21
来源:2014年高考数学(理)二轮专题复习知能提升演练选修4-4练习卷(带解析)
【题文】已知曲线
C1的参数方程为
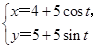
(
t为参数),以坐标原点为极点,
x轴的正半轴为极轴建立极坐标系,曲线
C2的极坐标方程为
ρ=2sin
θ.
(1)把
C1的参数方程化为极坐标方程;
(2)求
C1与
C2交点的极坐标(
ρ≥0,0≤
θ<2π).
题号:4187691
题型:解答题
难易度:一般
日期:2014-03-21
来源:2014年高考数学(理)二轮专题复习知能提升演练选修4-4练习卷(带解析)
【题文】在直角坐标系
xOy中,椭圆
C的参数方程为
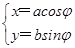
(
φ为参数,
a>
b>0),在极坐标系(与直角坐标系
xOy取相同的长度单位,且以原点
O为极点,以
x轴正半轴为极轴)中,直线
l与圆
O的极坐标方程分别为
ρsin(
θ+
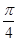
)=
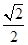 m
m(
m为非零数)与
ρ=
b.若直线
l经过椭圆
C的焦点,且与圆
O相切,求椭圆
C的离心率.
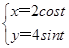 (t为参数),点M在椭圆上,对应参数t=
(t为参数),点M在椭圆上,对应参数t=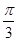 ,点O为原点,则直线OM的斜率为 ( ).
,点O为原点,则直线OM的斜率为 ( ).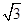
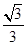
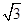
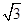
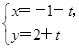 (t为参数)所表示的图形分别是( ).
(t为参数)所表示的图形分别是( ).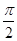 (ρ∈R)和ρcos θ=2
(ρ∈R)和ρcos θ=2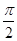 (ρ∈R)和ρcos θ=1
(ρ∈R)和ρcos θ=1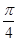 与曲线
与曲线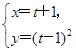 (t为参数)相交于A,B两点,则线段AB的中点的直角坐标为________.
(t为参数)相交于A,B两点,则线段AB的中点的直角坐标为________.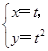 (t为参数),若以直角坐标系的原点为极点,x轴的正半轴为极轴建立极坐标系,则曲线C的极坐标方程为________.
(t为参数),若以直角坐标系的原点为极点,x轴的正半轴为极轴建立极坐标系,则曲线C的极坐标方程为________.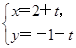 (t为参数)与曲线C
(t为参数)与曲线C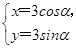 (α为参数)的交点个数为________.
(α为参数)的交点个数为________.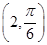 到直线ρsin θ=2的距离等于________.
到直线ρsin θ=2的距离等于________.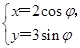 (φ为参数),以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,曲线C2的极坐标方程是ρ=2.正方形ABCD的顶点都在C2上,且A,B,C,D依逆时针次序排列,点A的极坐标为
(φ为参数),以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,曲线C2的极坐标方程是ρ=2.正方形ABCD的顶点都在C2上,且A,B,C,D依逆时针次序排列,点A的极坐标为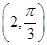 .
.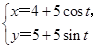 (t为参数),以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,曲线C2的极坐标方程为ρ=2sin θ.
(t为参数),以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,曲线C2的极坐标方程为ρ=2sin θ.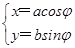 (φ为参数,a>b>0),在极坐标系(与直角坐标系xOy取相同的长度单位,且以原点O为极点,以x轴正半轴为极轴)中,直线l与圆O的极坐标方程分别为ρsin(θ+
(φ为参数,a>b>0),在极坐标系(与直角坐标系xOy取相同的长度单位,且以原点O为极点,以x轴正半轴为极轴)中,直线l与圆O的极坐标方程分别为ρsin(θ+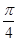 )=
)=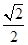 m(m为非零数)与ρ=b.若直线l经过椭圆C的焦点,且与圆O相切,求椭圆C的离心率.
m(m为非零数)与ρ=b.若直线l经过椭圆C的焦点,且与圆O相切,求椭圆C的离心率.