适用年级:{{getGradeNameByProperty('高三|专题试卷|全国|2014年')}} 试卷类型:{{getTestPaperTypeName('高三|专题试卷|全国|2014年')}} 使用省份:{{getAreaName('高三|专题试卷|全国|2014年')}}
试卷年份:{{getYear('高三|专题试卷|全国|2014年')}}上传日期:2014-03-16题数:14
提示:单击题文可显示答案与解析。
题号:948689
题型:选择题
难易度:一般
日期:2014-03-16
来源:2014年高考数学(理)二轮复习专题提升训练优化重组卷4练习卷(带解析)
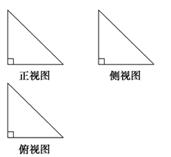
【题文】如图,某几何体的正视图、侧视图、俯视图均为直角三角形,则这个几何体的表面中,直角三角形个数为( ).
题号:948690
题型:选择题
难易度:较难
日期:2014-03-16
来源:2014年高考数学(理)二轮复习专题提升训练优化重组卷4练习卷(带解析)
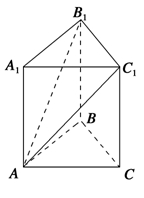
【题文】如图,在三棱柱
ABC-A1B1C1中,侧棱垂直于底面,底面是边长为2的等边三角形,侧棱长为3,则
BB1与平面
AB1C1所成的角为( ).
题号:948691
题型:选择题
难易度:一般
日期:2014-03-16
来源:2014年高考数学(理)二轮复习专题提升训练优化重组卷4练习卷(带解析)
题号:948712
题型:选择题
难易度:一般
日期:2014-03-16
来源:2014年高考数学(理)二轮复习专题提升训练优化重组卷4练习卷(带解析)
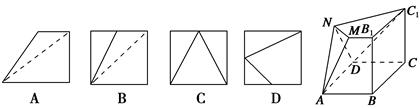
【题文】已知正方体
ABCD-A1B1C1D1,
M为棱
A1B1的中点,
N为棱
A1D1的中点.如图是该正方体被
M,
N,
A所确定的平面和
N,
D,
C1所确定的平面截去两个角后所得的几何体,则这个几何体的正视图为( ).
题号:4187786
题型:选择题
难易度:较难
日期:2014-03-20
来源:2014年高考数学(理)二轮复习专题提升训练优化重组卷4练习卷(带解析)
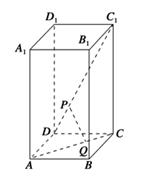
【题文】如图,在正四棱柱
ABCD-A1B1C1D1中,
AA1=2,
AB=
BC=1,动点
P,
Q分别在线段
C1D,
AC上,则线段
PQ长度的最小值是( ).
题号:948685
题型:填空题
难易度:一般
日期:2014-03-16
来源:2014年高考数学(理)二轮复习专题提升训练优化重组卷4练习卷(带解析)
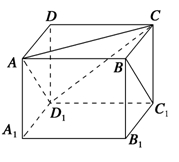
【题文】如图,在正方体
ABCD-A1B1C1D1中,点
P在直线
BC1上运动时,有下列三个命题:①三棱锥
AD1PC的体积不变;②直线
AP与平面
ACD1所成角的大小不变;③二面角
P-AD1-C的大小不变.其中真命题的序号是________.
题号:948686
题型:填空题
难易度:一般
日期:2014-03-16
来源:2014年高考数学(理)二轮复习专题提升训练优化重组卷4练习卷(带解析)
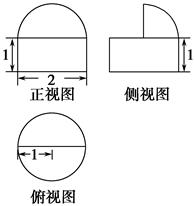
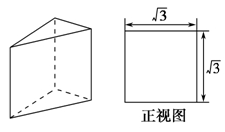
【题文】如图为某几何体的三视图,则该几何体的体积为________.
题号:948687
题型:填空题
难易度:较易
日期:2014-03-16
来源:2014年高考数学(理)二轮复习专题提升训练优化重组卷4练习卷(带解析)
【题文】一个圆锥和一个半球有公共底面,如果圆锥的体积和半球的体积相等,则这个圆锥的母线与轴所成角正弦值为________.
题号:948688
题型:填空题
难易度:一般
日期:2014-03-16
来源:2014年高考数学(理)二轮复习专题提升训练优化重组卷4练习卷(带解析)
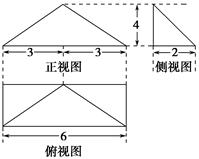
【题文】如图是某四棱锥的三视图,则该几何体的表面积为________.
题号:948684
题型:解答题
难易度:较难
日期:2014-03-16
来源:2014年高考数学(理)二轮复习专题提升训练优化重组卷4练习卷(带解析)
【题文】如图所示为一个几何体的直观图、三视图(其中正视图为直角梯形,俯视图为正方形,侧视图为直角三角形).
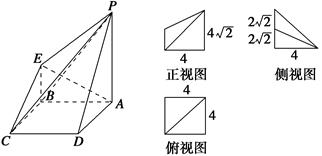
(1)求四棱锥
P-ABCD的体积;
(2)若
G为
BC上的动点,求证:
AE⊥
PG.
题号:4187787
题型:解答题
难易度:较难
日期:2014-03-18
来源:2014年高考数学(理)二轮复习专题提升训练优化重组卷4练习卷(带解析)
【题文】如图,在四棱锥
P-ABCD中,
PA⊥平面
ABCD,
E为
BD的中点,
G为
PD的中点,△
DAB≌△
DCB,
EA=
EB=
AB=1,
PA=
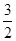
,连接
CE并延长交
AD于
F.
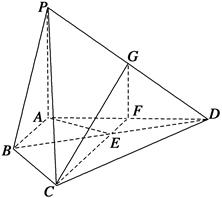
(1)求证:
AD⊥平面
CFG;
(2)求平面
BCP与平面
DCP的夹角的余弦值.
题号:4187788
题型:解答题
难易度:较难
日期:2014-03-18
来源:2014年高考数学(理)二轮复习专题提升训练优化重组卷4练习卷(带解析)
【题文】如图,四棱柱
ABCD-A1B1C1D1的底面
ABCD是正方形,
O为底面中心,
A1O⊥平面
ABCD,
AB=
AA1=
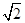
.
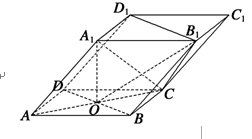
(1)证明:
A1C⊥平面
BB1D1D;
(2)求平面
OCB1与平面
BB1D1D的夹角
θ的大小.
题号:4187789
题型:解答题
难易度:较难
日期:2014-03-18
来源:2014年高考数学(理)二轮复习专题提升训练优化重组卷4练习卷(带解析)
【题文】如图,
ABCD是块矩形硬纸板,其中
AB=2
AD,
AD=
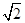
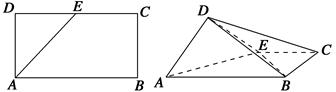
,
E为
DC的中点,将它沿
AE折成直二面角
D-AE-B.
(1)求证:
AD⊥平面
BDE;
(2)求二面角
B-AD-E的余弦值.
题号:4187790
题型:解答题
难易度:较难
日期:2014-03-18
来源:2014年高考数学(理)二轮复习专题提升训练优化重组卷4练习卷(带解析)
【题文】如图,在四棱锥
P-ABCD中,
PC⊥底面
ABCD,底面
ABCD是直角梯形,
AB⊥
AD,
AB∥
CD,
AB=2
AD=2
CD=2,
E是
PB的中点.
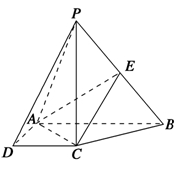
(1)求证:平面
EAC⊥平面
PBC;
(2)若二面角
P-AC-E的余弦值为
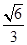
,求直线
PA与平面
EAC所成角的正弦值.


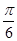
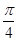
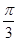
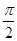
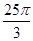
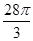


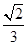
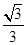
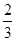
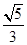




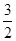 ,连接CE并延长交AD于F.
,连接CE并延长交AD于F.
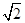 .
.
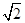 ,E为DC的中点,将它沿AE折成直二面角D-AE-B.
,E为DC的中点,将它沿AE折成直二面角D-AE-B.

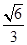 ,求直线PA与平面EAC所成角的正弦值.
,求直线PA与平面EAC所成角的正弦值.