适用年级:{{getGradeNameByProperty('高三|专题试卷|全国|2014年')}} 试卷类型:{{getTestPaperTypeName('高三|专题试卷|全国|2014年')}} 使用省份:{{getAreaName('高三|专题试卷|全国|2014年')}}
试卷年份:{{getYear('高三|专题试卷|全国|2014年')}}上传日期:2014-03-11题数:9
提示:单击题文可显示答案与解析。
题号:951092
题型:选择题
难易度:较易
日期:2014-03-11
来源:2014年高考数学(理)二轮复习4-1等差数列与等比数列练习卷(带解析)
【题文】已知等比数列{
an}中,
a1=1,且4
a2,2
a3,
a4成等差数列,则
a2+
a3+
a4等于 ( ).
题号:951093
题型:选择题
难易度:一般
日期:2014-03-11
来源:2014年高考数学(理)二轮复习4-1等差数列与等比数列练习卷(带解析)
【题文】设等比数列{
an}的公比
q=2,前
n项和为
Sn,若
S4=1,则
S8= ( ).
| A.17 | B.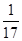 | C.5 | D.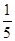 |
题号:951094
题型:选择题
难易度:较易
日期:2014-03-11
来源:2014年高考数学(理)二轮复习4-1等差数列与等比数列练习卷(带解析)
【题文】在等比数列{
an}中,已知
a1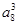 a15
a15=243,则
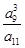
的值为( ).
题号:951096
题型:选择题
难易度:较易
日期:2014-03-11
来源:2014年高考数学(理)二轮复习4-1等差数列与等比数列练习卷(带解析)
【题文】已知数列{
an}为等差数列,且
a1+
a7+
a13=4π,则tan(
a2+
a12)= ( ).
题号:951069
题型:填空题
难易度:一般
日期:2014-03-11
来源:2014年高考数学(理)二轮复习4-1等差数列与等比数列练习卷(带解析)
【题文】设数列{an}是公差不为零的等差数列,Sn是数列{an}的前n项和,且S=9S2,S4=4S2,则数列{an}的通项公式为________.
题号:951070
题型:填空题
难易度:一般
日期:2014-03-11
来源:2014年高考数学(理)二轮复习4-1等差数列与等比数列练习卷(带解析)
【题文】若干个能唯一确定一个数列的量称为该数列的“基本量”.设{an}是公比为q的无穷等比数列,下列{an}的四组量中,一定能成为该数列“基本量”的是________.(写出所有符合要求的组号)
①S1与S2;②a2与S3;③a1与an;④q与an.其中n为大于1的整数,Sn为{an}的前n项和.
题号:951071
题型:填空题
难易度:较易
日期:2014-03-11
来源:2014年高考数学(理)二轮复习4-1等差数列与等比数列练习卷(带解析)
【题文】在等比数列{
an}中,若
a1=
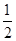
,
a4=-4,则|
a1|+|
a2|+…+|
an|=________.
题号:951067
题型:解答题
难易度:较难
日期:2014-03-11
来源:2014年高考数学(理)二轮复习4-1等差数列与等比数列练习卷(带解析)
【题文】设数列{an}的前n项和为Sn,已知ban-2n=(b-1)Sn.
(1)证明:当b=2时,{an-n·2n-1}是等比数列;
(2)求{an}的通项公式.
题号:951068
题型:解答题
难易度:较难
日期:2014-03-11
来源:2014年高考数学(理)二轮复习4-1等差数列与等比数列练习卷(带解析)
【题文】在等差数列{an}中,a16+a17+a18=a9=-36,其前n项和为Sn.
(1)求Sn的最小值,并求出Sn取最小值时n的值;
(2)求Tn=|a1|+|a2|+…+|an|.
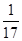
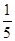
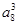 a15=243,则
a15=243,则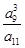 的值为( ).
的值为( ).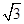
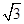
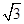
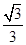
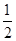 ,a4=-4,则|a1|+|a2|+…+|an|=________.
,a4=-4,则|a1|+|a2|+…+|an|=________.