适用年级:{{getGradeNameByProperty('高三|专题试卷|全国|2014年')}} 试卷类型:{{getTestPaperTypeName('高三|专题试卷|全国|2014年')}} 使用省份:{{getAreaName('高三|专题试卷|全国|2014年')}}
试卷年份:{{getYear('高三|专题试卷|全国|2014年')}}上传日期:2014-03-17题数:11
提示:单击题文可显示答案与解析。
题号:948590
题型:选择题
难易度:一般
日期:2014-03-17
来源:2014年高考数学(理)二轮专题复习知能提升演练1-1-3练习卷(带解析)
【题文】若变量
x,
y满足约束条件
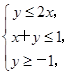
则
x+2
y的最大值是( ).
题号:948591
题型:选择题
难易度:较易
日期:2014-03-17
来源:2014年高考数学(理)二轮专题复习知能提升演练1-1-3练习卷(带解析)
【题文】若2
x+2
y=1,则
x+
y的取值范围是 ( ).
| A.[0,2] | B.[-2,0] |
| C.[-2,+∞) | D.(-∞,-2] |
题号:4187766
题型:选择题
难易度:一般
日期:2014-03-20
来源:2014年高考数学(理)二轮专题复习知能提升演练1-1-3练习卷(带解析)
【题文】小王从甲地到乙地往返的时速分别为
a和
b(
a<
b),其全程的平均时速为
v,则( ).
题号:4187767
题型:选择题
难易度:较易
日期:2014-03-20
来源:2014年高考数学(理)二轮专题复习知能提升演练1-1-3练习卷(带解析)
【题文】已知一元二次不等式
f(
x)<0的解集为
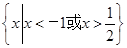
,则
f(10
x)>0的解集为( ).
| A.{x|x<-1或x>-lg 2} |
| B.{x|-1<x<-lg 2} |
| C.{x|x>-lg 2} |
| D.{x|x<-lg 2} |
题号:4187768
题型:选择题
难易度:一般
日期:2014-03-20
来源:2014年高考数学(理)二轮专题复习知能提升演练1-1-3练习卷(带解析)
【题文】某旅行社租用
A,
B两种型号的客车安排900名客人旅行,
A,
B两种车辆的载客量分别为36人和60人,租金分别为1 600元/辆和2 400元/辆,旅行社要求租车总数不超过21辆,且
B型车不多于
A型车7辆.则租金最少为( ).
| A.31 200元 | B.36 000元 |
| C.36 800元 | D.38 400元 |
题号:948589
题型:填空题
难易度:一般
日期:2014-03-17
来源:2014年高考数学(理)二轮专题复习知能提升演练1-1-3练习卷(带解析)
【题文】若点(x,y)位于曲线y=|x-1|与y=2所围成的封闭区域,则2x-y的最小值为________.
题号:4187769
题型:填空题
难易度:较易
日期:2014-03-20
来源:2014年高考数学(理)二轮专题复习知能提升演练1-1-3练习卷(带解析)
【题文】已知函数
f(
x)=4
x+
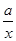
(
x>0,
a>0)在
x=3时取得最小值,则
a=________.
题号:4187770
题型:填空题
难易度:较易
日期:2014-03-20
来源:2014年高考数学(理)二轮专题复习知能提升演练1-1-3练习卷(带解析)
【题文】设0≤α≤π,不等式8x2-(8sin α)x+cos 2α≥0对x∈R恒成立,则α的取值范围是________.
题号:947828
题型:解答题
难易度:较难
日期:2014-03-22
来源:2014年高考数学(理)二轮专题复习知能提升演练1-1-3练习卷(带解析)
【题文】已知函数f(x)=x2+bx+c(b,c∈R),对任意的x∈R,恒有f′(x)≤f(x).
(1)证明:当x≥0时,f(x)≤(x+c)2;
(2)若对满足题设条件的任意b,c,不等式f(c)-f(b)≤M(c2-b2)恒成立,求M的最小值.
题号:4187771
题型:解答题
难易度:较难
日期:2014-03-20
来源:2014年高考数学(理)二轮专题复习知能提升演练1-1-3练习卷(带解析)
【题文】已知函数
f(
x)=
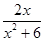
.
(1)若
f(
x)>
k的解集为{
x|
x<-3,或
x>-2},求
k的值;
(2)对任意
x>0,
f(
x)≤
t恒成立,求
t的取值范围.
题号:4817852
题型:解答题
难易度:一般
日期:2017-08-14
来源:2014年高考数学(理)二轮专题复习知能提升演练1-1-3练习卷(带解析)
【题文】为了在夏季降温和冬季供暖时减少能源损耗,房屋的屋顶和外墙需要建造隔热层,某幢建筑物要建造可使用20年的隔热层,每厘米厚的隔热层建造成本为6万元,该建筑物每年的能源消耗费用
C(单位:万元)与隔热层厚度
x(单位:cm)满足关系:
C(
x)=
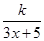
(0≤
x≤10),若不建隔热层,每年能源消耗费用为8万元.设
f(
x)为隔热层建造费用与20年的能源消耗费用之和.
(1)求
k的值及
f(
x)的表达式;
(2)隔热层修建多厚时,总费用
f(
x)达到最小,并求最小值.
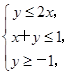 则x+2y的最大值是( ).
则x+2y的最大值是( ).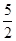
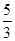
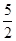
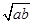
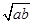
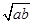 <v<
<v< 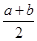
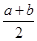
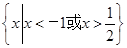 ,则f(10x)>0的解集为( ).
,则f(10x)>0的解集为( ).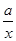 (x>0,a>0)在x=3时取得最小值,则a=________.
(x>0,a>0)在x=3时取得最小值,则a=________.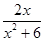 .
.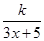 (0≤x≤10),若不建隔热层,每年能源消耗费用为8万元.设f(x)为隔热层建造费用与20年的能源消耗费用之和.
(0≤x≤10),若不建隔热层,每年能源消耗费用为8万元.设f(x)为隔热层建造费用与20年的能源消耗费用之和.