适用年级:{{getGradeNameByProperty('高三|专题试卷|全国|2014年')}} 试卷类型:{{getTestPaperTypeName('高三|专题试卷|全国|2014年')}} 使用省份:{{getAreaName('高三|专题试卷|全国|2014年')}}
试卷年份:{{getYear('高三|专题试卷|全国|2014年')}}上传日期:2014-03-11题数:10
提示:单击题文可显示答案与解析。
题号:951166
题型:选择题
难易度:较易
日期:2014-03-11
来源:2014年高考数学(理)二轮复习2-1函数的概念与基本初等函数练习卷(带解析)
【题文】函数
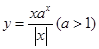
的图象的大致形状是()
题号:951167
题型:选择题
难易度:较易
日期:2014-03-11
来源:2014年高考数学(理)二轮复习2-1函数的概念与基本初等函数练习卷(带解析)
【题文】已知函数
f(
x)是定义在R上的奇函数,且当
x>0时,
f(
x)=2
x-3,则
f(-2)=( ).
| A.1 | B.-1 | C.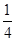 | D.-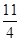 |
题号:951168
题型:选择题
难易度:较易
日期:2014-03-11
来源:2014年高考数学(理)二轮复习2-1函数的概念与基本初等函数练习卷(带解析)
题号:3628020
题型:选择题
难易度:较难
日期:2014-03-11
来源:2014年高考数学(理)二轮复习2-1函数的概念与基本初等函数练习卷(带解析)
【题文】直线
y=
x与函数
f(
x)=
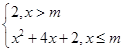
的图象恰有三个公共点,则实数
m的取值范围是 ( ).
| A.[-1,2) | B.[-1,2] | C.[2,+∞) | D.(-∞,-1] |
题号:3628021
题型:选择题
难易度:较难
日期:2014-03-11
来源:2014年高考数学(理)二轮复习2-1函数的概念与基本初等函数练习卷(带解析)
【题文】设
f(
x)与
g(
x)是定义在同一区间[
a,
b]上的两个函数,若函数
y=
f(
x)-
g(
x)在
x∈[
a,
b]上有两个不同的零点,则称
f(
x)和
g(
x)在[
a,
b]上是“关联函数”,区间[
a,
b]称为“关联区间”.若
f(
x)=
x2-3
x+4与
g(
x)=2
x+
m在[0,3]上是“关联函数”,则
m的取值范围是 ( ).
A.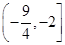 | B.[-1,0] | C.(-∞,-2] | D.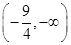 |
题号:951164
题型:填空题
难易度:较易
日期:2014-03-11
来源:2014年高考数学(理)二轮复习2-1函数的概念与基本初等函数练习卷(带解析)
【题文】已知定义在R上的函数
y=
f(
x)满足条件
f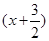
=-
f(
x),且函数
y=
f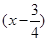
为奇函数,给出以下四个命题:
(1)函数
f(
x)是周期函数;
(2)函数
f(
x)的图象关于点
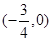
对称;
(3)函数
f(
x)为R上的偶函数;
(4)函数
f(
x)为R上的单调函数.
其中真命题的序号为________.(写出所有真命题的序号)
题号:951165
题型:填空题
难易度:容易
日期:2014-03-11
来源:2014年高考数学(理)二轮复习2-1函数的概念与基本初等函数练习卷(带解析)
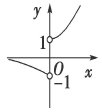
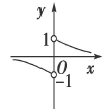
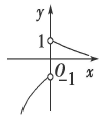
【题文】若函数
f(
x)=
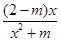
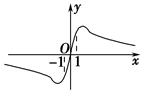
的图象如图,则
m的取值范围是________.
题号:3628022
题型:填空题
难易度:较难
日期:2014-03-11
来源:2014年高考数学(理)二轮复习2-1函数的概念与基本初等函数练习卷(带解析)
【题文】已知函数
f(
x)=
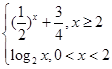
,若函数
g(
x)=
f(
x)-
k有两个不同的零点,则实数
k的取值范围是________.
题号:951162
题型:解答题
难易度:较难
日期:2014-03-11
来源:2014年高考数学(理)二轮复习2-1函数的概念与基本初等函数练习卷(带解析)
【题文】已知函数
f(
x)=
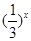
,
x∈[-1,1],函数
g(
x)=[
f(
x)]
2-2
af(
x)+3的最小值为
h(
a).
(1)求
h(
a);
(2)是否存在实数
m、
n同时满足下列条件:
①
m>
n>3;
②当
h(
a)的定义域为[
n,
m]时,值域为[
n2,
m2]?若存在,求出
m、
n的值;若不存在,说明理由.
题号:951163
题型:解答题
难易度:较难
日期:2014-03-11
来源:2014年高考数学(理)二轮复习2-1函数的概念与基本初等函数练习卷(带解析)
【题文】某养殖厂需定期购买饲料,已知该厂每天需要饲料200千克,每千克饲料的价格为1.8元,饲料的保管费与其他费用平均每千克每天0.03元,购买饲料每次支付运费300元.
(1)求该厂多少天购买一次饲料才能使平均每天支付的总费用最少;
(2)若提供饲料的公司规定,当一次购买饲料不少于5吨时,其价格可享受八五折优惠(即原价的85%).问:该厂是否应考虑利用此优惠条件?请说明理由.
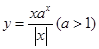 的图象的大致形状是()
的图象的大致形状是()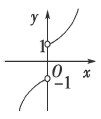
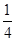
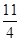
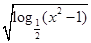 的定义域是 ( ).
的定义域是 ( ).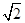 ,-1)∪(1,
,-1)∪(1,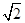 ]
]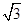 ,-1)∪(1,
,-1)∪(1,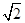 )
)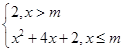 的图象恰有三个公共点,则实数m的取值范围是 ( ).
的图象恰有三个公共点,则实数m的取值范围是 ( ).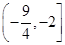
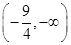
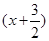 =-f(x),且函数y=f
=-f(x),且函数y=f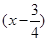 为奇函数,给出以下四个命题:
为奇函数,给出以下四个命题: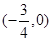 对称;
对称;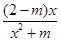 的图象如图,则m的取值范围是________.
的图象如图,则m的取值范围是________.
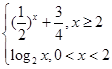 ,若函数g(x)=f(x)-k有两个不同的零点,则实数k的取值范围是________.
,若函数g(x)=f(x)-k有两个不同的零点,则实数k的取值范围是________.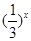 ,x∈[-1,1],函数g(x)=[f(x)]2-2af(x)+3的最小值为h(a).
,x∈[-1,1],函数g(x)=[f(x)]2-2af(x)+3的最小值为h(a).