适用年级:{{getGradeNameByProperty('高三|专题试卷|全国|2014年')}} 试卷类型:{{getTestPaperTypeName('高三|专题试卷|全国|2014年')}} 使用省份:{{getAreaName('高三|专题试卷|全国|2014年')}}
试卷年份:{{getYear('高三|专题试卷|全国|2014年')}}上传日期:2014-03-18题数:6
提示:单击题文可显示答案与解析。
题号:947883
题型:解答题
难易度:较难
日期:2014-03-18
来源:2014届高考数学(文)三轮专题体系通关训练解答题押题练C组练习卷(带解析)
【题文】设数列{
bn}满足
bn+2=-
bn+1-
bn(
n∈N
*),
b2=2
b1.
(1)若
b3=3,求
b1的值;
(2)求证数列{
bnbn+1bn+2+
n}是等差数列;
(3)设数列{
Tn}满足:
Tn+1=
Tnbn+1(
n∈N
*),且
T1=
b1=-
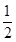
,若存在实数
p,
q,对任意
n∈N
*都有
p≤
T1+
T2+
T3+…+
Tn<
q成立,试求
q-
p的最小值.
题号:947884
题型:解答题
难易度:较难
日期:2014-03-18
来源:2014届高考数学(文)三轮专题体系通关训练解答题押题练C组练习卷(带解析)
【题文】已知函数f(x)=x2-(1+2a)x+aln x(a为常数).
(1)当a=-1时,求曲线y=f(x)在x=1处切线的方程;
(2)当a>0时,讨论函数y=f(x)在区间(0,1)上的单调性,并写出相应的单调区间.
题号:947885
题型:解答题
难易度:困难
日期:2014-03-18
来源:2014届高考数学(文)三轮专题体系通关训练解答题押题练C组练习卷(带解析)
【题文】已知椭圆
C:
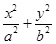
=1(
a>
b>0)上任一点
P到两个焦点的距离的和为2
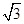
,
P与椭圆长轴两顶点连线的斜率之积为-
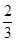
.设直线
l过椭圆
C的右焦点
F,交椭圆
C于两点
A(
x1,
y1),
B(
x2,
y2).
(1)若
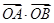
=
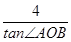
(
O为坐标原点),求|
y1-
y2|的值;
(2)当直线
l与两坐标轴都不垂直时,在
x轴上是否总存在点
Q,使得直线
QA,
QB的倾斜角互为补角?若存在,求出点
Q坐标;若不存在,请说明理由.
题号:947886
题型:解答题
难易度:一般
日期:2014-03-18
来源:2014届高考数学(文)三轮专题体系通关训练解答题押题练C组练习卷(带解析)
【题文】某创业投资公司拟投资开发某种新能源产品,估计能获得10万元到1 000万元的投资收益.现准备制定一个对科研课题组的奖励方案:资金
y(单位:万元)随投资收益
x(单位:万元)的增加而增加,且奖金不超过9万元,同时奖金不超过投资收益的20%.
(1)若建立函数
y=
f(
x)模型制定奖励方案,试用数学语言表述该公司对奖励函数
f(
x)模型的基本要求,并分析函数
y=
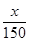
+2是否符合公司要求的奖励函数模型,并说明原因;
(2)若该公司采用模型函数
y=
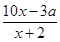
作为奖励函数模型,试确定最小的正整数
a的值.
题号:947887
题型:解答题
难易度:较易
日期:2014-03-18
来源:2014届高考数学(文)三轮专题体系通关训练解答题押题练C组练习卷(带解析)
【题文】如图,在四棱锥
P
ABCD中,
PA⊥底面
ABCD,
AC⊥
CD,∠
DAC=60°,
AB=
BC=
AC,
E是
PD的中点,
F为
ED的中点.
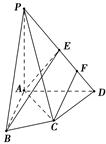
(1)求证:平面
PAC⊥平面
PCD;
(2)求证:
CF∥平面
BAE.
题号:947888
题型:解答题
难易度:一般
日期:2014-03-18
来源:2014届高考数学(文)三轮专题体系通关训练解答题押题练C组练习卷(带解析)
【题文】已知向量
m=
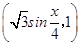
,
n=
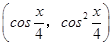
.
(1)若
m·n=1,求cos
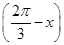
的值;
(2)记
f(
x)=
m·n,在△
ABC中,角
A,
B,
C的对边分别是
a,
b,
c,且满足(2
a-
c)cos
B=
bcos
C,求函数
f(
A)的取值范围.
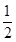 ,若存在实数p,q,对任意n∈N*都有p≤T1+T2+T3+…+Tn<q成立,试求q-p的最小值.
,若存在实数p,q,对任意n∈N*都有p≤T1+T2+T3+…+Tn<q成立,试求q-p的最小值.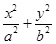 =1(a>b>0)上任一点P到两个焦点的距离的和为2
=1(a>b>0)上任一点P到两个焦点的距离的和为2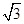 ,P与椭圆长轴两顶点连线的斜率之积为-
,P与椭圆长轴两顶点连线的斜率之积为-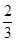 .设直线l过椭圆C的右焦点F,交椭圆C于两点A(x1,y1),B(x2,y2).
.设直线l过椭圆C的右焦点F,交椭圆C于两点A(x1,y1),B(x2,y2).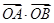 =
=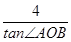 (O为坐标原点),求|y1-y2|的值;
(O为坐标原点),求|y1-y2|的值;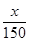 +2是否符合公司要求的奖励函数模型,并说明原因;
+2是否符合公司要求的奖励函数模型,并说明原因;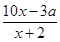 作为奖励函数模型,试确定最小的正整数a的值.
作为奖励函数模型,试确定最小的正整数a的值.
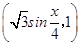 ,n=
,n=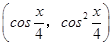 .
.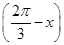 的值;
的值;