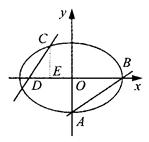
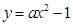 上总存在两点关于直线
上总存在两点关于直线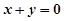 对称,则实数
对称,则实数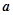 的取值范围是
的取值范围是A.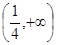 | B.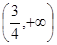 | C.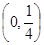 | D.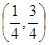 |
A.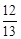 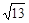 | B.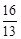 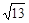 | C.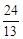 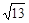 | D.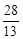 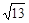 |
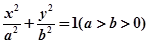 的右焦点的弦为直径的圆与直线
的右焦点的弦为直径的圆与直线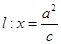 的位置关系是
的位置关系是| A.相交 | B.相切 | C.相离 | D.不能确定 |
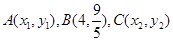 是右焦点为
是右焦点为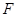 的椭圆
的椭圆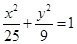 上三个不同的点,则“
上三个不同的点,则“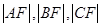 成等差数列”是“
成等差数列”是“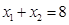 ”的
”的| A.充要条件 | B.必要不充分条件 |
| C.充分不必要条件 | D.既非充分也非必要 |
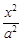 +
+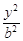 =1中心的弦,F(c,0)为椭圆的右焦点,则△AFB面积的最大值是
=1中心的弦,F(c,0)为椭圆的右焦点,则△AFB面积的最大值是| A.b2 | B.ab | C.ac | D.bc |
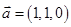 ,
,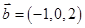 ,且
,且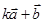 与
与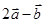 互相垂直,则
互相垂直,则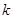 的值是()
的值是()| A.1 | B.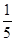 | C.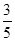 | D.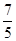 |
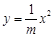 的焦点坐标为
的焦点坐标为A.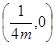 | B.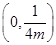 | C.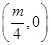 | D.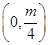 |
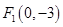 ,
,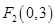 ,动点
,动点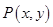 满足条件
满足条件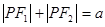
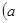 >
>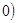 ,则动点
,则动点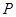 的轨迹是
的轨迹是| A.椭圆 | B.线段 |
| C.不存在 | D.椭圆或线段或不存在 |
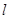 与双曲线
与双曲线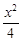 -
-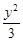 =-1有两个交点,则直线
=-1有两个交点,则直线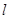 的斜率的取值范围是
的斜率的取值范围是A.(-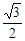 , ,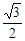 ) ) | B.(-∞,-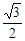 )∪( )∪(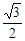 ,+∞) ,+∞) |
C.[-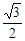 , ,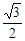 ] ] | D.(-∞,-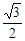 ]∪[ ]∪[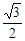 ,+∞) ,+∞) |
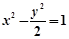 的右焦点作直线
的右焦点作直线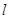 ,交双曲线于A、B两点,若|AB|=
,交双曲线于A、B两点,若|AB|= 4,则这样的直线的条数为
4,则这样的直线的条数为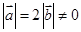 ,且关于
,且关于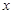 的方程
的方程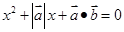 有实根,则
有实根,则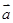 与
与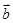 夹角的取值
夹角的取值 范围是( ).
范围是( ).A.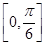 | B.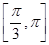 | C.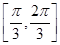 | D.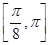 |
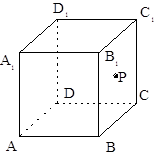
| A.直线 | B.抛物线 | C.双曲线 | D.圆 |
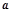 的线段AB的两个端点A、B都在抛物线
的线段AB的两个端点A、B都在抛物线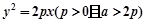 上滑动,则线段AB的中点M到
上滑动,则线段AB的中点M到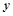 轴的最短距离是
轴的最短距离是 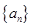 的前
的前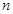 项和
项和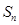 ,若
,若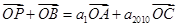 ,且
,且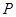 、
、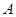 、
、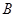 、
、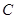 四点共面(
四点共面(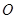 为该平面外一点),则
为该平面外一点),则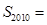 .
.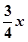 ,则此双曲线的离心率为________.
,则此双曲线的离心率为________.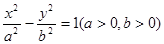 的焦点,过
的焦点,过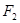 作垂直于
作垂直于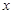 轴的直线交双曲线与点P且∠P F1F2=300,求双曲线的渐近线方程.
轴的直线交双曲线与点P且∠P F1F2=300,求双曲线的渐近线方程.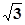 ,求此椭圆的标准方程。
,求此椭圆的标准方程。 原点,它的准线过双曲线
原点,它的准线过双曲线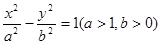 的一个焦点,并于双曲线的实轴垂直,已知抛物线与双曲线的交点为
的一个焦点,并于双曲线的实轴垂直,已知抛物线与双曲线的交点为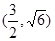 ,求抛物线的方程和双曲线的方程。
,求抛物线的方程和双曲线的方程。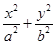 (a>b>0)的离心率
(a>b>0)的离心率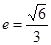 ,过点A(0,-b)和B(a,0)的直线与原点的距离为
,过点A(0,-b)和B(a,0)的直线与原点的距离为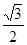 .
.