适用年级:{{getGradeNameByProperty('初三|同步测试|全国|2015年')}} 试卷类型:{{getTestPaperTypeName('初三|同步测试|全国|2015年')}} 使用省份:{{getAreaName('初三|同步测试|全国|2015年')}}
试卷年份:{{getYear('初三|同步测试|全国|2015年')}}上传日期:2015-03-06题数:30
提示:单击题文可显示答案与解析。
题号:616768
题型:填空题
难易度:一般
日期:2015-03-06
来源:2015年课时同步练习(浙教版)九年级上1.3二次函数的性质2(带解析)
【题文】函数y=﹣
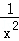
+
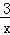
的最大值为
.
题号:616769
题型:填空题
难易度:一般
日期:2015-03-06
来源:2015年课时同步练习(浙教版)九年级上1.3二次函数的性质2(带解析)
【题文】已知实数x、y满足x2﹣2x+4y=5,则x+2y的最大值为 .
题号:616770
题型:填空题
难易度:一般
日期:2015-03-06
来源:2015年课时同步练习(浙教版)九年级上1.3二次函数的性质2(带解析)
【题文】请你写出一个二次函数,使其同时满足下列条件:①在对称轴的右侧y随x的增大而减小;②与y轴交于点(0,﹣2);③经过点(1,0).答 .
题号:616771
题型:填空题
难易度:一般
日期:2015-03-06
来源:2015年课时同步练习(浙教版)九年级上1.3二次函数的性质2(带解析)
【题文】请你写出一个你学习过的函数表达式,使它满足当1<x<2时,﹣2<y<﹣1.你写的函数是
.
题号:616772
题型:填空题
难易度:一般
日期:2015-03-06
来源:2015年课时同步练习(浙教版)九年级上1.3二次函数的性质2(带解析)
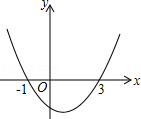
【题文】根据图中的抛物线可以判断:当x
时,y随x的增大而减小.
题号:616773
题型:填空题
难易度:一般
日期:2015-03-06
来源:2015年课时同步练习(浙教版)九年级上1.3二次函数的性质2(带解析)
【题文】二次函数y=﹣2(x﹣1)(x﹣3)的图象的对称轴是 .
题号:616774
题型:填空题
难易度:一般
日期:2015-03-06
来源:2015年课时同步练习(浙教版)九年级上1.3二次函数的性质2(带解析)
【题文】如图,已知抛物线
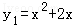
和直线y
2=x.我们约定:当x任取一值时,x对应的函数值k分别为y
1、y
2,若y
1≠y
2,取y
1、y
2中的较大值记为M;若y
1=y
2,记M=y
1=y
2.下列判断:
①当x<﹣1时,M=y
1;②当x<0时,x值越大,M值越大;
③使得M<﹣1的x值不存在;④使M=2的x值有2个.
其中正确的是
.(填序号)
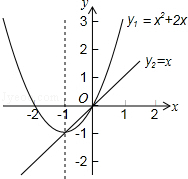
题号:616775
题型:填空题
难易度:一般
日期:2015-03-06
来源:2015年课时同步练习(浙教版)九年级上1.3二次函数的性质2(带解析)
【题文】请写出一个关于二次函数y=x2﹣2x﹣3图象或性质的结论: .
题号:616776
题型:填空题
难易度:一般
日期:2015-03-06
来源:2015年课时同步练习(浙教版)九年级上1.3二次函数的性质2(带解析)
【题文】已知抛物线的顶点坐标为(﹣1,﹣2),且通过点(1,10),则该抛物线的解析式为 .
题号:616777
题型:填空题
难易度:一般
日期:2015-03-06
来源:2015年课时同步练习(浙教版)九年级上1.3二次函数的性质2(带解析)
【题文】函数y=﹣2(x﹣1)2+3的最大值为 .
题号:616778
题型:填空题
难易度:一般
日期:2015-03-06
来源:2015年课时同步练习(浙教版)九年级上1.3二次函数的性质2(带解析)
【题文】已知抛物线的表达式是y=2(x+2)2﹣1,那么它的顶点坐标是 .
题号:616779
题型:填空题
难易度:一般
日期:2015-03-06
来源:2015年课时同步练习(浙教版)九年级上1.3二次函数的性质2(带解析)
【题文】抛物线y=(x﹣2)2+5的顶点坐标是 .
题号:616780
题型:填空题
难易度:一般
日期:2015-03-06
来源:2015年课时同步练习(浙教版)九年级上1.3二次函数的性质2(带解析)
【题文】已知函数y=mx

,当m=
时,它的图象是开口向下的抛物线,且当x=
时,y随x的增大而增大.
题号:616781
题型:填空题
难易度:一般
日期:2015-03-06
来源:2015年课时同步练习(浙教版)九年级上1.3二次函数的性质2(带解析)
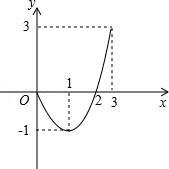
【题文】已知二次函数的图象(0≤x≤3)如图所示,则当0≤x≤3时,函数值y的范围是
.
题号:616782
题型:填空题
难易度:一般
日期:2015-03-06
来源:2015年课时同步练习(浙教版)九年级上1.3二次函数的性质2(带解析)
【题文】已知抛物线y=x2﹣2x﹣3与y轴交于点C,则点C的坐标是 ;若点C′是点的C关于该抛物线的对称轴对称点,则C′点的坐标是 .
题号:616783
题型:填空题
难易度:一般
日期:2015-03-06
来源:2015年课时同步练习(浙教版)九年级上1.3二次函数的性质2(带解析)
【题文】观察二次函数y=x2﹣2x﹣1的图象,若x>0,则y的取值范围是 .
题号:616784
题型:填空题
难易度:一般
日期:2015-03-06
来源:2015年课时同步练习(浙教版)九年级上1.3二次函数的性质2(带解析)
【题文】抛物线y=x2+4x﹣3的对称轴是直线 .
题号:616785
题型:填空题
难易度:一般
日期:2015-03-06
来源:2015年课时同步练习(浙教版)九年级上1.3二次函数的性质2(带解析)
题号:616786
题型:填空题
难易度:一般
日期:2015-03-06
来源:2015年课时同步练习(浙教版)九年级上1.3二次函数的性质2(带解析)
【题文】抛物线y=﹣2(x+4)2的对称轴是直线 .
题号:616787
题型:填空题
难易度:一般
日期:2015-03-06
来源:2015年课时同步练习(浙教版)九年级上1.3二次函数的性质2(带解析)
【题文】若二次函数y=x2﹣3x+2m的最小值是2,则m= .
题号:616788
题型:填空题
难易度:一般
日期:2015-03-06
来源:2015年课时同步练习(浙教版)九年级上1.3二次函数的性质2(带解析)
【题文】请写出一个以(﹣1,2)为顶点,且开口向上的二次函数 .
题号:616760
题型:解答题
难易度:一般
日期:2015-03-06
来源:2015年课时同步练习(浙教版)九年级上1.3二次函数的性质2(带解析)
【题文】直线y=2x+3与抛物线y=ax2交于A、B两点,已知A点的横坐标是3,求A、B两点的坐标及抛物线的解析式.
题号:616761
题型:解答题
难易度:一般
日期:2015-03-06
来源:2015年课时同步练习(浙教版)九年级上1.3二次函数的性质2(带解析)
【题文】已知反比例函数y=
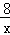
与一次函数y=kx﹣2的图象都经过点A(a,﹣4),且一次函数y=kx﹣2的图象与x轴交于点B.
(1)求a、k的值;
(2)若抛物线y=x
2+bx+c过点A、B,求此抛物线的解析式.
题号:616762
题型:解答题
难易度:一般
日期:2015-03-06
来源:2015年课时同步练习(浙教版)九年级上1.3二次函数的性质2(带解析)
【题文】根据条件求下列抛物线的解析式:
(1)二次函数的图象经过(0,1),(2,1)和(3,4);
(2)抛物线的顶点坐标是(﹣2,1),且经过点(1,﹣2).
题号:616763
题型:解答题
难易度:一般
日期:2015-03-06
来源:2015年课时同步练习(浙教版)九年级上1.3二次函数的性质2(带解析)
【题文】如图,二次函数y=ax
2+bx+c的图象过A、B、C三点.
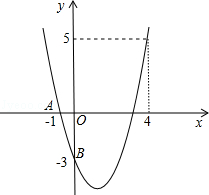
(1)求出抛物线解析式和顶点坐标;
(2)当﹣2<x<2时,求函数值y的范围;
(3)根据图象回答,当x取何值时,y>0?
题号:616764
题型:解答题
难易度:一般
日期:2015-03-06
来源:2015年课时同步练习(浙教版)九年级上1.3二次函数的性质2(带解析)
【题文】如图为抛物线y=﹣x
2+bx+c的一部分,它经过A(﹣1,0),B(0,3)两点.
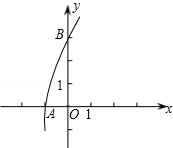
(1)求抛物线的解析式;
(2)将此抛物线向左平移3个单位,再向下平移1个单位,求平移后的抛物线的解析式.
题号:616765
题型:解答题
难易度:一般
日期:2015-03-06
来源:2015年课时同步练习(浙教版)九年级上1.3二次函数的性质2(带解析)
【题文】一个二次函数的图象经过点(0,0),(﹣1,﹣1),(1,9)三点,求这个函数的关系式.
题号:616766
题型:解答题
难易度:一般
日期:2015-03-06
来源:2015年课时同步练习(浙教版)九年级上1.3二次函数的性质2(带解析)
【题文】已知抛物线y=x2+(2m+1)x+m+1,根据下列条件分别求m的值.
(1)若抛物线过原点;
(2)若抛物线的顶点在x轴上;
(3)若抛物线的对称轴为x=1.
题号:616767
题型:解答题
难易度:一般
日期:2015-03-06
来源:2015年课时同步练习(浙教版)九年级上1.3二次函数的性质2(带解析)
【题文】如果函数y=a(x﹣1)2+c与函数y=x2+2bx+b2﹣5的顶点相同,且其中一个函数经过点(2,7),求这两个函数的解析式.
题号:3935665
题型:解答题
难易度:一般
日期:2015-03-06
来源:2015年课时同步练习(浙教版)九年级上1.3二次函数的性质2(带解析)
【题文】已知二次函数y=ax2+bx﹣3的图象经过点A(2,﹣3),B(﹣1,0).求二次函数的解析式.
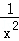 +
+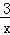 的最大值为 .
的最大值为 .
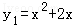 和直线y2=x.我们约定:当x任取一值时,x对应的函数值k分别为y1、y2,若y1≠y2,取y1、y2中的较大值记为M;若y1=y2,记M=y1=y2.下列判断:
和直线y2=x.我们约定:当x任取一值时,x对应的函数值k分别为y1、y2,若y1≠y2,取y1、y2中的较大值记为M;若y1=y2,记M=y1=y2.下列判断: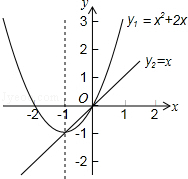
 ,当m= 时,它的图象是开口向下的抛物线,且当x= 时,y随x的增大而增大.
,当m= 时,它的图象是开口向下的抛物线,且当x= 时,y随x的增大而增大.
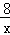 与一次函数y=kx﹣2的图象都经过点A(a,﹣4),且一次函数y=kx﹣2的图象与x轴交于点B.
与一次函数y=kx﹣2的图象都经过点A(a,﹣4),且一次函数y=kx﹣2的图象与x轴交于点B.
