适用年级:{{getGradeNameByProperty('高三|专题试卷|全国|2014年')}} 试卷类型:{{getTestPaperTypeName('高三|专题试卷|全国|2014年')}} 使用省份:{{getAreaName('高三|专题试卷|全国|2014年')}}
试卷年份:{{getYear('高三|专题试卷|全国|2014年')}}上传日期:2014-03-26题数:15
提示:单击题文可显示答案与解析。
题号:946058
题型:选择题
难易度:较难
日期:2014-03-26
来源:2014年高考数学理复习方案二轮作业手册新课标·通用版专题四练习卷(带解析)
【题文】已知函数
f(
x)是R上的单调递增函数且为奇函数,数列{
an}是等差数列,
a3>0,则
f(
a1)+
f(
a3)+
f(
a5)的值( )
| A.恒为正数 |
| B.恒为负数 |
| C.恒为0 |
| D.可以为正数也可以为负数 |
题号:946059
题型:选择题
难易度:较难
日期:2014-03-26
来源:2014年高考数学理复习方案二轮作业手册新课标·通用版专题四练习卷(带解析)
【题文】设等差数列{
an}的前
n项和是
Sn,若-
am<
a1<-
am+1(
m∈N
*,且
m≥2),则必定有( )
| A.Sm>0且Sm+1<0 | B.Sm<0且Sm+1>0 | C.Sm>0且Sm+1>0 | D.Sm<0且Sm+1<0 |
题号:946060
题型:选择题
难易度:较易
日期:2014-03-26
来源:2014年高考数学理复习方案二轮作业手册新课标·通用版专题四练习卷(带解析)
【题文】已知等比数列{
an}满足
a1=2,
a3a5=4
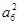
,则
a3的值为( )
A.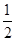 | B.1 | C.2 | D.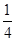 |
题号:946061
题型:选择题
难易度:较易
日期:2014-03-26
来源:2014年高考数学理复习方案二轮作业手册新课标·通用版专题四练习卷(带解析)
【题文】已知{
an}为等差数列,若
a3+
a4+
a8=9,则
S9=( )
题号:946062
题型:选择题
难易度:较易
日期:2014-03-26
来源:2014年高考数学理复习方案二轮作业手册新课标·通用版专题四练习卷(带解析)
【题文】已知等比数列{a
n}中,有a
3a
11=4a
7,数列{b
n}是等差数列,且b
7=a
7,则b
5+b
9等于()
题号:946063
题型:选择题
难易度:一般
日期:2014-03-26
来源:2014年高考数学理复习方案二轮作业手册新课标·通用版专题四练习卷(带解析)
【题文】{
an}为首项为正数的递增等差数列,其前
n项和为
Sn,则点(
n,
Sn)所在的抛物线可能为( )
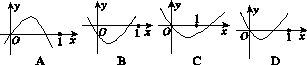
题号:946064
题型:选择题
难易度:一般
日期:2014-03-26
来源:2014年高考数学理复习方案二轮作业手册新课标·通用版专题四练习卷(带解析)
【题文】已知等差数列{
an}的前
n项和为
Sn,且
S3=6,则5
a1+
a7的值为( )
题号:946065
题型:选择题
难易度:较易
日期:2014-03-26
来源:2014年高考数学理复习方案二轮作业手册新课标·通用版专题四练习卷(带解析)
【题文】公比为2的等比数列{
an}的各项都是正数,且
a4a10=16,则
a6=( )
题号:946054
题型:填空题
难易度:一般
日期:2014-03-26
来源:2014年高考数学理复习方案二轮作业手册新课标·通用版专题四练习卷(带解析)
【题文】在数列{an}中,a1=1,a2=2,若当整数n>1时,Sn+1+Sn-1=2(Sn+S1)恒成立,则S15=________.
题号:946055
题型:填空题
难易度:一般
日期:2014-03-26
来源:2014年高考数学理复习方案二轮作业手册新课标·通用版专题四练习卷(带解析)
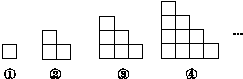
【题文】如图所示的图形由小正方形组成,请观察图①至图④的规律,并依此规律,得第
n个图形中小正方形的个数是________.
题号:946056
题型:填空题
难易度:较易
日期:2014-03-26
来源:2014年高考数学理复习方案二轮作业手册新课标·通用版专题四练习卷(带解析)
【题文】已知数列1,
a1,
a2,9是等差数列,数列1,
b1,
b2,
b3,9是等比数列,则
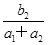
的值为________.
题号:946057
题型:填空题
难易度:较易
日期:2014-03-26
来源:2014年高考数学理复习方案二轮作业手册新课标·通用版专题四练习卷(带解析)
【题文】在等比数列{an}中,a1+a2=20,a3+a4=40,则a5+a6等于________.
题号:946031
题型:解答题
难易度:一般
日期:2014-03-26
来源:2014年高考数学理复习方案二轮作业手册新课标·通用版专题四练习卷(带解析)
【题文】已知
n∈N
*,数列{
dn}满足
dn=
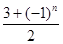
,数列{
an}满足
an=
d1+
d2+
d3+…+
d2n.又知数列{
bn}中,
b1=2,且对任意正整数
m,
n,
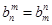
.
(1)求数列{
an}和数列{
bn}的通项公式;
(2)将数列{
bn}中的第
a1项,第
a2项,第
a3项,…,第
an项删去后,剩余的项按从小到大的顺序排成新数列{
cn},求数列{
cn}的前2013项和
T2013.
题号:946052
题型:解答题
难易度:较难
日期:2014-03-26
来源:2014年高考数学理复习方案二轮作业手册新课标·通用版专题四练习卷(带解析)
【题文】数列{
an}的前
n项和为
Sn=2
an-2,数列{
bn}是首项为
a1,公差不为零的等差数列,且
b1,
b3,
b11成等比数列.
(1)求数列{
an}与{
bn}的通项公式;
(2)求证:
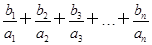
<5.
题号:946053
题型:解答题
难易度:较难
日期:2014-03-26
来源:2014年高考数学理复习方案二轮作业手册新课标·通用版专题四练习卷(带解析)
【题文】已知等比数列{an}的所有项均为正数,首项a1=1,且a4,3a3,a5成等差数列.
(1)求数列{an}的通项公式;
(2)数列{an+1-λan}的前n项和为Sn,若Sn=2n-1(n∈N*),求实数λ的值.
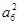 ,则a3的值为( )
,则a3的值为( )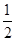
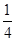
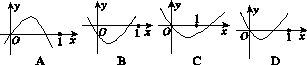

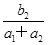 的值为________.
的值为________.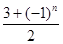 ,数列{an}满足an=d1+d2+d3+…+d2n.又知数列{bn}中,b1=2,且对任意正整数m,n,
,数列{an}满足an=d1+d2+d3+…+d2n.又知数列{bn}中,b1=2,且对任意正整数m,n,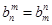 .
. 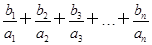 <5.
<5.