适用年级:{{getGradeNameByProperty('高三|专题试卷|全国|2014年')}} 试卷类型:{{getTestPaperTypeName('高三|专题试卷|全国|2014年')}} 使用省份:{{getAreaName('高三|专题试卷|全国|2014年')}}
试卷年份:{{getYear('高三|专题试卷|全国|2014年')}}上传日期:2014-03-17题数:11
提示:单击题文可显示答案与解析。
题号:924680
题型:选择题
难易度:较易
日期:2014-05-08
来源:2014年高考数学(理)二轮专题复习知能提升演练1-5-2练习卷(带解析)
【题文】设l是直线,α,β是两个不同的平面( )
| A.若l//α,l//β,则α//β |
| B.若l//α,l⊥β,则α⊥β |
| C.若α⊥β,l⊥α,则l⊥β |
| D.若α⊥β,l//α,则l⊥β |
题号:948439
题型:选择题
难易度:较易
日期:2014-03-17
来源:2014年高考数学(理)二轮专题复习知能提升演练1-5-2练习卷(带解析)
【题文】如图所示,在四边形
ABCD中,
AD∥
BC,
AD=
AB,∠
BCD=45°,∠
BAD=90°.将△
ADB沿
BD折起,使平面
ABD⊥平面
BCD,构成三棱锥
A-
BCD.则在三棱锥
A-
BCD中,下列命题正确的是( ).
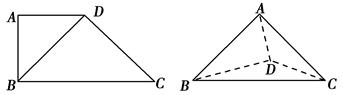
| A.平面ABD⊥平面ABC |
| B.平面ADC⊥平面BDC |
| C.平面ABC⊥平面BDC |
| D.平面ADC⊥平面ABC |
题号:948440
题型:选择题
难易度:容易
日期:2014-03-17
来源:2014年高考数学(理)二轮专题复习知能提升演练1-5-2练习卷(带解析)
【题文】设
a,
b是不同的直线,
α,
β是不同的平面,则下列命题:
①若
a⊥
b,
a∥
α,则
b∥
α;②若
a∥
α,
α⊥
β,则
a⊥
β;
③若
a⊥
β,
α⊥
β,则
a∥
α;④若
a⊥
b,
a⊥
α,
b⊥
β,则
α⊥
β.
其中正确命题的个数是 ( ).
题号:4187741
题型:选择题
难易度:较难
日期:2014-03-20
来源:2014年高考数学(理)二轮专题复习知能提升演练1-5-2练习卷(带解析)
【题文】已知三棱柱
ABC-
A1B1C1的侧棱与底面垂直,体积为
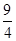
,底面是边长为
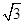
的正三角形.若
P为底面
A1B1C1的中心,则
PA与平面
ABC所成角的大小为 ( ).
题号:4187742
题型:选择题
难易度:一般
日期:2014-03-20
来源:2014年高考数学(理)二轮专题复习知能提升演练1-5-2练习卷(带解析)
【题文】如图所示,四棱锥
S-
ABCD的底面为正方形,
SD⊥底面
ABCD,则下列结论中不正确的是 ( ).
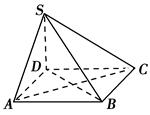
| A.AC⊥SB |
| B.AB∥平面SCD |
| C.SA与平面SBD所成的角等于SC与平面SBD所成的角 |
| D.AB与SC所成的角等于DC与SA所成的角 |
题号:948438
题型:填空题
难易度:较难
日期:2014-03-17
来源:2014年高考数学(理)二轮专题复习知能提升演练1-5-2练习卷(带解析)
【题文】如图,正方体
ABCD-
A1B1C1D1的棱长为1,
P为
BC的中点,
Q为线段
CC1上的动点,过点
A,
P,
Q的平面截该正方体所得的截面记为
S.则下列命题正确的是________(写出所有正确命题的编号).
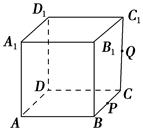
①当0<
CQ<
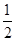
时,
S为四边形;
②当
CQ=
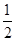
时,
S为等腰梯形;
③当
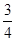
<
CQ<1时,
S为六边形;
④当
CQ=1时,
S的面积为
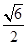
.
题号:4187743
题型:填空题
难易度:一般
日期:2014-03-20
来源:2014年高考数学(理)二轮专题复习知能提升演练1-5-2练习卷(带解析)
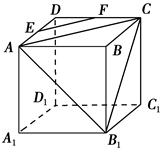
【题文】如图,在正方体
ABCD-
A1B1C1D1中,
AB=2,点
E为
AD的中点,点
F在
CD上.若
EF∥平面
AB1C,则线段
EF的长度等于________.
题号:4187744
题型:填空题
难易度:一般
日期:2014-03-20
来源:2014年高考数学(理)二轮专题复习知能提升演练1-5-2练习卷(带解析)
【题文】如图,
PA⊥⊙
O所在的平面,
AB是⊙
O的直径,
C是⊙
O上的一点,
E,
F分别是点
A在
PB,
PC上的射影,给出下列结论:
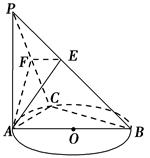
①
AF⊥
PB;②
EF⊥
PB;③
AF⊥
BC;④
AE⊥平面
PBC.其中正确命题的序号是________.
题号:948436
题型:解答题
难易度:较难
日期:2014-03-17
来源:2014年高考数学(理)二轮专题复习知能提升演练1-5-2练习卷(带解析)
【题文】在直角梯形
ABCD中,
AB∥
CD,
AD⊥
AB,
CD=2
AB=4,
AD=
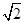
,
E为
CD的中点,将△
BCE沿
BE折起,使得
CO⊥
DE,其中垂足
O在线段
DE内.
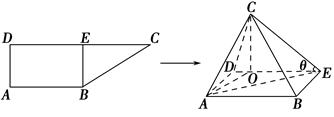
(1)求证:
CO⊥平面
ABED;
(2)问∠
CEO(记为
θ)多大时,三棱锥
C-
AOE的体积最大,最大值为多少.
题号:948437
题型:解答题
难易度:较难
日期:2014-03-17
来源:2014年高考数学(理)二轮专题复习知能提升演练1-5-2练习卷(带解析)
【题文】如图,
AB是圆
O的直径,
PA垂直圆
O所在的平面,
C是圆
O上的点.
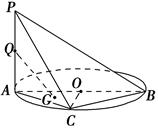
(1)求证:
BC⊥平面
PAC;
(2)设
Q为
PA的中点,
G为△
AOC的重心,求证:
QG∥平面
PBC.
题号:4187745
题型:解答题
难易度:一般
日期:2014-03-21
来源:2014年高考数学(理)二轮专题复习知能提升演练1-5-2练习卷(带解析)
【题文】如图,在三棱柱
ABC-
A1B1C1中,
CA=
CB,
AB=
AA1,∠
BAA1=60°.
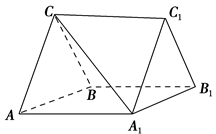
(1)证明:
AB⊥
A1C;
(2)若
AB=
CB=2,
A1C=
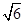
,求三棱柱
ABC-
A1B1C1的体积;
(3)若平面
ABC⊥平面
AA1B1B,
AB=
CB=2,求直线
A1C与平面
BB1C1C所成角的正弦值.

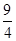 ,底面是边长为
,底面是边长为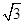 的正三角形.若P为底面A1B1C1的中心,则PA与平面ABC所成角的大小为 ( ).
的正三角形.若P为底面A1B1C1的中心,则PA与平面ABC所成角的大小为 ( ).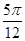
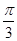
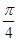
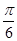


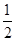 时,S为四边形;
时,S为四边形;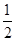 时,S为等腰梯形;
时,S为等腰梯形;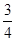 <CQ<1时,S为六边形;
<CQ<1时,S为六边形;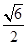 .
.

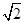 ,E为CD的中点,将△BCE沿BE折起,使得CO⊥DE,其中垂足O在线段DE内.
,E为CD的中点,将△BCE沿BE折起,使得CO⊥DE,其中垂足O在线段DE内.


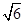 ,求三棱柱ABC-A1B1C1的体积;
,求三棱柱ABC-A1B1C1的体积;