适用年级:{{getGradeNameByProperty('高三|专题试卷|全国|2014年')}} 试卷类型:{{getTestPaperTypeName('高三|专题试卷|全国|2014年')}} 使用省份:{{getAreaName('高三|专题试卷|全国|2014年')}}
试卷年份:{{getYear('高三|专题试卷|全国|2014年')}}上传日期:2014-03-17题数:11
提示:单击题文可显示答案与解析。
题号:948484
题型:选择题
难易度:较易
日期:2014-03-17
来源:2014年高考数学(理)二轮专题复习知能提升演练1-4-1练习卷(带解析)
【题文】公比为2的等比数列{
an}的各项都是正数,且
a3a11=16,则log
2a10=( ).
题号:948485
题型:选择题
难易度:较易
日期:2014-03-17
来源:2014年高考数学(理)二轮专题复习知能提升演练1-4-1练习卷(带解析)
【题文】设等差数列{
an}的前
n项和为
Sn,
Sm-1=-2,
Sm=0,
Sm+1=3,则
m等于( ).
题号:948486
题型:选择题
难易度:一般
日期:2014-03-17
来源:2014年高考数学(理)二轮专题复习知能提升演练1-4-1练习卷(带解析)
【题文】已知{
an}为等比数列,下面结论中正确的是( ).
| A.a1+a3≥2a2 | B.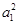 + +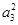 ≥2 ≥2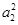 |
| C.若a1=a3,则a1=a2 | D.若a3>a1,则a4>a2 |
题号:948487
题型:选择题
难易度:一般
日期:2014-03-17
来源:2014年高考数学(理)二轮专题复习知能提升演练1-4-1练习卷(带解析)
【题文】等比数列{
an}的前
n项和为
Sn,已知
S3=
a2+10
a1,
a5=9,则
a1 ( ).
题号:948488
题型:选择题
难易度:较易
日期:2014-03-17
来源:2014年高考数学(理)二轮专题复习知能提升演练1-4-1练习卷(带解析)
【题文】在等差数列{
an}中,
a1+
a5=10,
a4=7,则数列{
an}的公差为( )
题号:948481
题型:填空题
难易度:一般
日期:2014-03-17
来源:2014年高考数学(理)二轮专题复习知能提升演练1-4-1练习卷(带解析)
【题文】将全体正整数排成一个三角形数阵:
1
2 3
4 5 6
7 8 9 10
11 12 13 14 15
……
根据以上排列规律,数阵中第n(n≥3)行从左至右的第3个数是________.
题号:948482
题型:填空题
难易度:较易
日期:2014-03-17
来源:2014年高考数学(理)二轮专题复习知能提升演练1-4-1练习卷(带解析)
【题文】已知{an}是等差数列,a1=1,公差d≠0,Sn为其前n项和,若a1,a2,a5成等比数列,则S8=________.
题号:948483
题型:填空题
难易度:较易
日期:2014-03-17
来源:2014年高考数学(理)二轮专题复习知能提升演练1-4-1练习卷(带解析)
【题文】等差数列{an}前9项的和等于前4项的和.若a4+ak=0,则k=________.
题号:948478
题型:解答题
难易度:较难
日期:2014-03-17
来源:2014年高考数学(理)二轮专题复习知能提升演练1-4-1练习卷(带解析)
【题文】已知等比数列{
an}满足:|
a2-
a3|=10,
a1a2a3=125.
(1)求数列{
an}的通项公式;
(2)是否存在正整数
m,使得
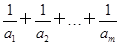
≥1?若存在,求
m的最小值;若不存在,说明理由.
题号:948479
题型:解答题
难易度:较难
日期:2014-03-17
来源:2014年高考数学(理)二轮专题复习知能提升演练1-4-1练习卷(带解析)
【题文】设{an}是公比大于1的等比数列,Sn为数列{an}的前n项和.已知S3=7,且a1+3,3a2,a3+4构成等差数列.
(1)求数列{an}的通项公式;
(2)令bn=ln a3n+1,n=1,2,…,求数列{bn}的前n项和Tn.
题号:948480
题型:解答题
难易度:较难
日期:2014-03-17
来源:2014年高考数学(理)二轮专题复习知能提升演练1-4-1练习卷(带解析)
【题文】设{an}是公比不为1的等比数列,其前n项和为Sn,且a5,a3,a4成等差数列.
(1)求数列{an}的公比;
(2)证明:对任意k∈N*,Sk+2,Sk,Sk+1成等差数列.
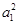 +
+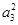 ≥2
≥2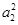
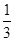
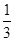
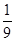
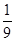
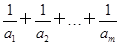 ≥1?若存在,求m的最小值;若不存在,说明理由.
≥1?若存在,求m的最小值;若不存在,说明理由.