适用年级:{{getGradeNameByProperty('高三|专题试卷|全国|2014年')}} 试卷类型:{{getTestPaperTypeName('高三|专题试卷|全国|2014年')}} 使用省份:{{getAreaName('高三|专题试卷|全国|2014年')}}
试卷年份:{{getYear('高三|专题试卷|全国|2014年')}}上传日期:2014-04-08题数:20
提示:单击题文可显示答案与解析。
题号:938174
题型:填空题
难易度:一般
日期:2014-04-08
来源:2014届高考数学总复习考点引领+技巧点拨第二章第14课时练习卷(带解析)
【题文】对于实数a和b,定义运算“”:ab=
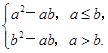
设f(x)=(2x-1)(x-1),且关于x的方程为f(x)=m(m∈R)恰有三个互不相等的实数根x
1,x
2,x
3,则x
1、x
2、x
3的取值范围是________.
题号:938175
题型:填空题
难易度:一般
日期:2014-04-08
来源:2014届高考数学总复习考点引领+技巧点拨第二章第14课时练习卷(带解析)
【题文】已知函数f(x)=
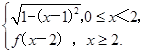
若关于x的方程f(x)=kx(k>0)有且仅有四个根,其最大根为t,则函数g(t)=
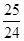
t
2-6t+7的值域为________.
题号:938176
题型:填空题
难易度:一般
日期:2014-04-08
来源:2014届高考数学总复习考点引领+技巧点拨第二章第14课时练习卷(带解析)
【题文】已知函数f(x)=2x2+m的图象与函数g(x)=ln|x|的图象有四个交点,则实数m的取值范围是________.
题号:938181
题型:填空题
难易度:一般
日期:2014-04-08
来源:2014届高考数学总复习考点引领+技巧点拨第二章第14课时练习卷(带解析)
【题文】关于函数f(x)=lg
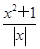
(x>0,x∈R),下列命题正确的是________.(填序号)
①函数y=f(x)的图象关于y轴对称;
②在区间(-∞,0)上,函数y=f(x)是减函数;
③函数y=f(x)的最小值为lg2;
④在区间(1,+∞)上,函数y=f(x)是增函数.
题号:938183
题型:填空题
难易度:一般
日期:2014-04-08
来源:2014届高考数学总复习考点引领+技巧点拨第二章第14课时练习卷(带解析)
【题文】已知函数f(x)=||x-1|-1|,若关于x的方程f(x)=m(m∈R)恰有四个互不相等的实根x1,x2,x3,x4,则x1x2x3x4的取值范围是________.
题号:938184
题型:填空题
难易度:较难
日期:2014-04-08
来源:2014届高考数学总复习考点引领+技巧点拨第二章第14课时练习卷(带解析)
【题文】已知函数y=f(x)是偶函数,对于x∈R都有f(x+6)=f(x)+f(3)成立.当x
1、x
2∈[0,3],且x
1≠x
2时,都有
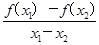
>0,给出下列命题:
①f(3)=0;
②直线x=-6是函数y=f(x)的图象的一条对称轴;
③函数y=f(x)在[-9,-6]上为单调增函数;
④函数y=f(x)在[-9,9]上有4个零点.
其中正确的命题是________.(填序号)
题号:938185
题型:填空题
难易度:一般
日期:2014-04-08
来源:2014届高考数学总复习考点引领+技巧点拨第二章第14课时练习卷(带解析)
【题文】若函数f(x)=
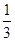
x
3-
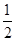
ax
2+(a-1)x+1在区间(1,4)上是减函数,在区间(6,+∞)上是增函数,则实数a的取值范围是________.
题号:938186
题型:填空题
难易度:容易
日期:2014-04-08
来源:2014届高考数学总复习考点引领+技巧点拨第二章第14课时练习卷(带解析)
【题文】已知a、b为正实数,函数f(x)=ax3+bx+2x在[0,1]上的最大值为4,则f(x)在[-1,0]上的最小值为________.
题号:938187
题型:填空题
难易度:较易
日期:2014-04-08
来源:2014届高考数学总复习考点引领+技巧点拨第二章第14课时练习卷(带解析)
【题文】已知集合A={x|33-x<6},B={x|lg(x-1)<1},则A∩B=________.
题号:4186898
题型:填空题
难易度:一般
日期:2014-04-10
来源:2014届高考数学总复习考点引领+技巧点拨第二章第14课时练习卷(带解析)
【题文】在平面直角坐标系xOy中,设定点A(a,a),P是函数y=
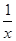
(x>0)图象上一动点.若点P、A之间的最短距离为2
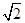
,则满足条件的实数a的所有值为________.
题号:4186899
题型:填空题
难易度:一般
日期:2014-04-10
来源:2014届高考数学总复习考点引领+技巧点拨第二章第14课时练习卷(带解析)
【题文】设函数f(x)=
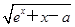
(a∈R,e为自然对数的底数).若存在b∈[0,1]使f(f(b))=b成立,则a的取值范围是________.
题号:4186900
题型:填空题
难易度:较易
日期:2014-04-10
来源:2014届高考数学总复习考点引领+技巧点拨第二章第14课时练习卷(带解析)
【题文】若奇函数f(x)与偶函数g(x)满足f(x)+g(x)=2x,则函数g(x)的最小值是________.
题号:4186901
题型:填空题
难易度:较易
日期:2014-04-10
来源:2014届高考数学总复习考点引领+技巧点拨第二章第14课时练习卷(带解析)
【题文】设函数f(x)=
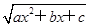
(a<0)的定义域为D,若所有点(s,f(t))(s、t∈D)构成一个正方形区域,则a的值为________.
题号:938173
题型:解答题
难易度:较难
日期:2014-04-08
来源:2014届高考数学总复习考点引领+技巧点拨第二章第14课时练习卷(带解析)
【题文】已知函数f(x)=lnx-ax
2+(2-a)x.
(1)讨论f(x)的单调性;
(2)设a>0,证明:当0<x<
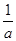
时,f
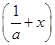
>f
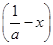
;
(3)若函数y=f(x)的图象与x轴交于A、B两点,线段AB中点的横坐标为x
0,证明:
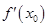
<0.
题号:938177
题型:解答题
难易度:较难
日期:2014-04-08
来源:2014届高考数学总复习考点引领+技巧点拨第二章第14课时练习卷(带解析)
【题文】已知函数f(x)=ax+x2-xlna(a>0,a≠1).
(1)当a>1时,求证:函数f(x)在(0,+∞)上单调递增;
(2)若函数y=|f(x)-t|-1有三个零点,求t的值;
(3)若存在x1、x2∈[-1,1],使得|f(x1)-f(x2)|≥e-1,试求a的取值范围.
题号:938178
题型:解答题
难易度:较难
日期:2014-04-08
来源:2014届高考数学总复习考点引领+技巧点拨第二章第14课时练习卷(带解析)
【题文】已知f(x)=xlnx,g(x)=-x
2+ax-3.
(1)求函数f(x)在[t,t+2](t>0)上的最小值;
(2)对一切x∈(0,+∞),2f(x)≥g(x)恒成立,求实数a的取值范围;
(3)证明对一切x∈(0,+∞),都有lnx>
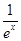
-
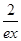
成立.
题号:938179
题型:解答题
难易度:一般
日期:2014-04-08
来源:2014届高考数学总复习考点引领+技巧点拨第二章第14课时练习卷(带解析)
【题文】设函数f(x)=
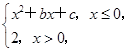
其中b>0,c∈R.当且仅当x=-2时,函数f(x)取得最小值-2.
(1)求函数f(x)的表达式;
(2)若方程f(x)=x+a(a∈R)至少有两个不相同的实数根,求a取值的集合.
题号:938180
题型:解答题
难易度:一般
日期:2014-04-08
来源:2014届高考数学总复习考点引领+技巧点拨第二章第14课时练习卷(带解析)
【题文】已知函数f(x)=ax
2-|x|+2a-1(a为实常数).
(1)若a=1,作函数f(x)的图象;
(2)设f(x)在区间[1,2]上的最小值为g(a),求g(a)的表达式;
(3)设h(x)=
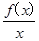
,若函数h(x)在区间[1,2]上是增函数,求实数a的取值范围.
题号:938182
题型:解答题
难易度:一般
日期:2014-04-08
来源:2014届高考数学总复习考点引领+技巧点拨第二章第14课时练习卷(带解析)
【题文】已知函数f(x)=lg(1-x)+lg(1+x)+x4-2x2.
(1)求函数f(x)的定义域;
(2)判断函数f(x)的奇偶性;
(3)求函数f(x)的值域.
题号:4186897
题型:解答题
难易度:较难
日期:2014-04-10
来源:2014届高考数学总复习考点引领+技巧点拨第二章第14课时练习卷(带解析)
【题文】定义在D上的函数f(x),如果满足:对任意x∈D,存在常数M>0,都有|f(x)|≤M成立,则称f(x)是D上的有界函数,其中M称为函数f(x)的上界.已知函数f(x)=1+a·
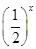
+
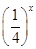
.
(1)当a=1时,求函数f(x)在(-∞,0)上的值域,并判断函数f(x)在(-∞,0)上是否为有界函数,请说明理由;
(2)若函数f(x)在[0,+∞)上是以3为上界的有界函数,求实数a的取值范围.
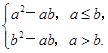 设f(x)=(2x-1)(x-1),且关于x的方程为f(x)=m(m∈R)恰有三个互不相等的实数根x1,x2,x3,则x1、x2、x3的取值范围是________.
设f(x)=(2x-1)(x-1),且关于x的方程为f(x)=m(m∈R)恰有三个互不相等的实数根x1,x2,x3,则x1、x2、x3的取值范围是________.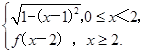 若关于x的方程f(x)=kx(k>0)有且仅有四个根,其最大根为t,则函数g(t)=
若关于x的方程f(x)=kx(k>0)有且仅有四个根,其最大根为t,则函数g(t)=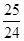 t2-6t+7的值域为________.
t2-6t+7的值域为________.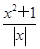 (x>0,x∈R),下列命题正确的是________.(填序号)
(x>0,x∈R),下列命题正确的是________.(填序号)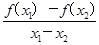 >0,给出下列命题:
>0,给出下列命题: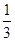 x3-
x3-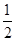 ax2+(a-1)x+1在区间(1,4)上是减函数,在区间(6,+∞)上是增函数,则实数a的取值范围是________.
ax2+(a-1)x+1在区间(1,4)上是减函数,在区间(6,+∞)上是增函数,则实数a的取值范围是________.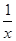 (x>0)图象上一动点.若点P、A之间的最短距离为2
(x>0)图象上一动点.若点P、A之间的最短距离为2 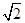 ,则满足条件的实数a的所有值为________.
,则满足条件的实数a的所有值为________.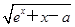 (a∈R,e为自然对数的底数).若存在b∈[0,1]使f(f(b))=b成立,则a的取值范围是________.
(a∈R,e为自然对数的底数).若存在b∈[0,1]使f(f(b))=b成立,则a的取值范围是________.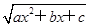 (a<0)的定义域为D,若所有点(s,f(t))(s、t∈D)构成一个正方形区域,则a的值为________.
(a<0)的定义域为D,若所有点(s,f(t))(s、t∈D)构成一个正方形区域,则a的值为________.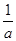 时,f
时,f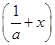 >f
>f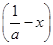 ;
;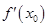 <0.
<0.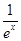 -
-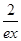 成立.
成立.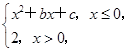 其中b>0,c∈R.当且仅当x=-2时,函数f(x)取得最小值-2.
其中b>0,c∈R.当且仅当x=-2时,函数f(x)取得最小值-2.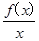 ,若函数h(x)在区间[1,2]上是增函数,求实数a的取值范围.
,若函数h(x)在区间[1,2]上是增函数,求实数a的取值范围.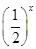 +
+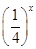 .
.