适用年级:{{getGradeNameByProperty('高三|专题试卷|全国|2014年')}} 试卷类型:{{getTestPaperTypeName('高三|专题试卷|全国|2014年')}} 使用省份:{{getAreaName('高三|专题试卷|全国|2014年')}}
试卷年份:{{getYear('高三|专题试卷|全国|2014年')}}上传日期:2014-03-22题数:11
提示:单击题文可显示答案与解析。
题号:947653
题型:填空题
难易度:较难
日期:2014-03-22
来源:2014年高考数学(文)二轮复习专题提升训练江苏专用11练习卷(带解析)
【题文】直线
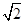 ax
ax+
by=1与圆
x2+
y2=1相交于
A,
B两点(其中
a,
b是实数),且△
AOB是直角三角形(
O是坐标原点),则点
P(
a,
b)与点(0,1)之间距离的最小值为________.
题号:947654
题型:填空题
难易度:较易
日期:2014-03-22
来源:2014年高考数学(文)二轮复习专题提升训练江苏专用11练习卷(带解析)
【题文】若直线ax+by=1过点A(b,a),则以坐标原点O为圆心,OA长为半径的圆的面积的最小值是________.
题号:947655
题型:填空题
难易度:一般
日期:2014-03-22
来源:2014年高考数学(文)二轮复习专题提升训练江苏专用11练习卷(带解析)
【题文】在平面直角坐标系中,设直线
l:
kx-
y+
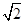
=0与圆
C:
x2+
y2=4相交于
A、
B两点,
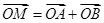
,若点
M在圆
C上,则实数
k=________.
题号:947656
题型:填空题
难易度:一般
日期:2014-03-22
来源:2014年高考数学(文)二轮复习专题提升训练江苏专用11练习卷(带解析)
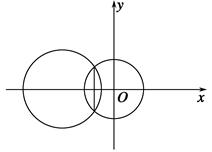
【题文】若圆
x2+
y2=4与圆
x2+
y2+2
ax-6=0(
a>0)的公共弦的长为2
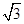
,则
a=________.
题号:947658
题型:填空题
难易度:一般
日期:2014-03-22
来源:2014年高考数学(文)二轮复习专题提升训练江苏专用11练习卷(带解析)
【题文】已知圆(x-a)2+(y-b)2=r2的圆心为抛物线y2=4x的焦点,且与直线3x+4y+2=0相切,则该圆的方程为________.
题号:947659
题型:填空题
难易度:一般
日期:2014-03-22
来源:2014年高考数学(文)二轮复习专题提升训练江苏专用11练习卷(带解析)
【题文】已知直线
x-
y+
a=0与圆
x2+
y2=1交于
A、
B两点,且向量
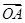
、
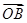
满足|
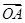
+
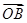
|=|
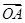
-
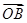
|,其中
O为坐标原点,则实数
a的值为______.
题号:947660
题型:填空题
难易度:一般
日期:2014-03-22
来源:2014年高考数学(文)二轮复习专题提升训练江苏专用11练习卷(带解析)
【题文】若圆x2+y2+2x-4y+1=0关于直线2ax-by+2=0(a,b∈R)对称,则ab的取值范围是________.
题号:3916433
题型:填空题
难易度:一般
日期:2017-07-26
来源:2014年高考数学(文)二轮复习专题提升训练江苏专用11练习卷(带解析)
【题文】已知圆的方程为
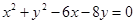
,设该圆过点(3,5)的最长弦和最短弦分别为
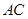
和
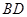
,则四边形
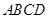
的面积为__________.
题号:947652
题型:解答题
难易度:较难
日期:2014-03-22
来源:2014年高考数学(文)二轮复习专题提升训练江苏专用11练习卷(带解析)
【题文】已知双曲线
x2-
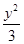
=1.
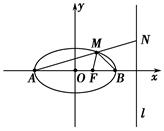
(1)若一椭圆与该双曲线共焦点,且有一交点
P(2,3),求椭圆方程.
(2)设(1)中椭圆的左、右顶点分别为
A、
B,右焦点为
F,直线
l为椭圆的右准线,
N为
l上的一动点,且在
x轴上方,直线
AN与椭圆交于点
M.若
AM=
MN,求∠
AMB的余弦值;
(3)设过
A、
F、
N三点的圆与
y轴交于
P、
Q两点,当线段
PQ的中点为(0,9)时,求这个圆的方程.
题号:4187624
题型:解答题
难易度:较难
日期:2014-03-23
来源:2014年高考数学(文)二轮复习专题提升训练江苏专用11练习卷(带解析)
【题文】已知点A(-3,0),B(3,0),动点P满足|PA|=2|PB|.
(1)若点P的轨迹为曲线C,求此曲线的方程;
(2)若点Q在直线l1:x+y+3=0上,直线l2经过点Q且与曲线C只有一个公共点M,求|QM|的最小值.
题号:4187625
题型:解答题
难易度:较难
日期:2014-03-23
来源:2014年高考数学(文)二轮复习专题提升训练江苏专用11练习卷(带解析)
【题文】已知以点
C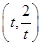
(
t∈R,
t≠0)为圆心的圆与
x轴交于点
O,
A,与
y轴交于点
O,
B,其中
O为原点.
(1)求证:△
AOB的面积为定值;
(2)设直线2
x+
y-4=0与圆
C交于点
M,
N,若|
OM|=|
ON|,求圆
C的方程;
(3)在(2)的条件下,设
P,
Q分别是直线
l:
x+
y+2=0和圆
C上的动点,求|
PB|+|
PQ|的最小值及此时点
P的坐标..
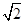 ax+by=1与圆x2+y2=1相交于A,B两点(其中a,b是实数),且△AOB是直角三角形(O是坐标原点),则点P(a,b)与点(0,1)之间距离的最小值为________.
ax+by=1与圆x2+y2=1相交于A,B两点(其中a,b是实数),且△AOB是直角三角形(O是坐标原点),则点P(a,b)与点(0,1)之间距离的最小值为________.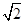 =0与圆C:x2+y2=4相交于A、B两点,
=0与圆C:x2+y2=4相交于A、B两点,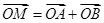 ,若点M在圆C上,则实数k=________.
,若点M在圆C上,则实数k=________.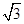 ,则a=________.
,则a=________.
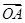 、
、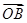 满足|
满足| 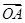 +
+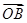 |=|
|=| 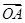 -
-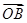 |,其中O为坐标原点,则实数a的值为______.
|,其中O为坐标原点,则实数a的值为______.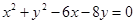 ,设该圆过点(3,5)的最长弦和最短弦分别为
,设该圆过点(3,5)的最长弦和最短弦分别为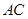 和
和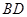 ,则四边形
,则四边形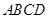 的面积为__________.
的面积为__________.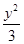 =1.
=1.
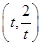 (t∈R,t≠0)为圆心的圆与x轴交于点O,A,与y轴交于点O,B,其中O为原点.
(t∈R,t≠0)为圆心的圆与x轴交于点O,A,与y轴交于点O,B,其中O为原点.