适用年级:{{getGradeNameByProperty('高三|专题试卷|全国|2014年')}} 试卷类型:{{getTestPaperTypeName('高三|专题试卷|全国|2014年')}} 使用省份:{{getAreaName('高三|专题试卷|全国|2014年')}}
试卷年份:{{getYear('高三|专题试卷|全国|2014年')}}上传日期:2014-03-18题数:6
提示:单击题文可显示答案与解析。
题号:947889
题型:解答题
难易度:较难
日期:2014-03-18
来源:2014届高考数学(文)三轮专题体系通关训练解答题押题练B组练习卷(带解析)
【题文】已知数列{
an}的前三项分别为
a1=5,
a2=6,
a3=8,且数列{
an}的前
n项和
Sn满足
Sn+m=
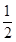
(
S2n+
S2m)-(
n-
m)
2,其中
m,
n为任意正整数.
(1)求数列{
an}的通项公式及前
n项和
Sn;
(2)求满足
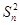
-
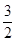 an
an+33=
k2的所有正整数
k,
n.
题号:947890
题型:解答题
难易度:较难
日期:2014-03-18
来源:2014届高考数学(文)三轮专题体系通关训练解答题押题练B组练习卷(带解析)
【题文】已知函数
f(
x)=-
x3+
x2,
g(
x)=
aln
x,
a∈R.
(1)若对任意
x∈[1,e],都有
g(
x)≥-
x2+(
a+2)
x恒成立,求
a的取值范围;
(2)设
F(
x)=
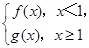
若
P是曲线
y=
F(
x)上异于原点
O的任意一点,在曲线
y=
F(
x)上总存在另一点
Q,使得△
POQ中的∠
POQ为钝角,且
PQ的中点在
y轴上,求
a的取值范围.
题号:947891
题型:解答题
难易度:困难
日期:2014-03-18
来源:2014届高考数学(文)三轮专题体系通关训练解答题押题练B组练习卷(带解析)
【题文】如图,椭圆
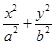
=1(
a>
b>0)的上,下两个顶点为
A,
B,直线
l:
y=-2,点
P是椭圆上异于点
A,
B的任意一点,连接
AP并延长交直线
l于点
N,连接
PB并延长交直线
l于点
M,设
AP所在的直线的斜率为
k1,
BP所在的直线的斜率为
k2.若椭圆的离心率为
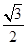
,且过点
A(0,1).
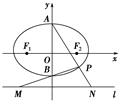
(1)求
k1·
k2的值;
(2)求
MN的最小值;
(3)随着点
P的变化,以
MN为直径的圆是否恒过定点?若过定点,求出该定点;如不过定点,请说明理由.
题号:947932
题型:解答题
难易度:一般
日期:2014-03-18
来源:2014届高考数学(文)三轮专题体系通关训练解答题押题练B组练习卷(带解析)
【题文】某商场对
A品牌的商品进行了市场调查,预计2012年从1月起前
x个月顾客对
A品牌的商品的需求总量
P(
x)件与月份
x的近似关系是:
P(
x)=
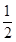 x
x(
x+1)(41-2
x)(
x≤12且
x∈N
*)
(1)写出第
x月的需求量
f(
x)的表达式;
(2)若第
x月的销售量
g(
x)=
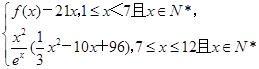
(单位:件),每件利润
q(
x)元与月份
x的近似关系为:
q(
x)=
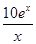
,问:该商场销售
A品牌商品,预计第几月的月利润达到最大值?月利润最大值是多少?(e
6≈403)
题号:947933
题型:解答题
难易度:一般
日期:2014-03-18
来源:2014届高考数学(文)三轮专题体系通关训练解答题押题练B组练习卷(带解析)
【题文】如图,在四棱锥
P
ABCD中,
PA⊥底面
ABCD,
PC⊥
AD,底面
ABCD为梯形,
AB∥
DC,
AB⊥
BC,
PA=
AB=
BC,点
E在棱
PB上,且
PE=2
EB.
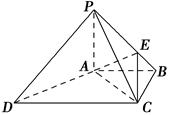
(1)求证:平面
PAB⊥平面
PCB;
(2)求证:
PD∥平面
EAC.
题号:4187639
题型:解答题
难易度:一般
日期:2014-03-20
来源:2014届高考数学(文)三轮专题体系通关训练解答题押题练B组练习卷(带解析)
【题文】设向量
a=(2,sin
θ),
b=(1,cos
θ),
θ为锐角.
(1)若
a·b=
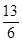
,求sin
θ+cos
θ的值;
(2)若
a∥
b,求sin
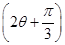
的值.
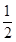 (S2n+S2m)-(n-m)2,其中m,n为任意正整数.
(S2n+S2m)-(n-m)2,其中m,n为任意正整数.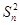 -
-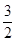 an+33=k2的所有正整数k,n.
an+33=k2的所有正整数k,n.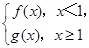 若P是曲线y=F(x)上异于原点O的任意一点,在曲线y=F(x)上总存在另一点Q,使得△POQ中的∠POQ为钝角,且PQ的中点在y轴上,求a的取值范围.
若P是曲线y=F(x)上异于原点O的任意一点,在曲线y=F(x)上总存在另一点Q,使得△POQ中的∠POQ为钝角,且PQ的中点在y轴上,求a的取值范围.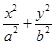 =1(a>b>0)的上,下两个顶点为A,B,直线l:y=-2,点P是椭圆上异于点A,B的任意一点,连接AP并延长交直线l于点N,连接PB并延长交直线l于点M,设AP所在的直线的斜率为k1,BP所在的直线的斜率为k2.若椭圆的离心率为
=1(a>b>0)的上,下两个顶点为A,B,直线l:y=-2,点P是椭圆上异于点A,B的任意一点,连接AP并延长交直线l于点N,连接PB并延长交直线l于点M,设AP所在的直线的斜率为k1,BP所在的直线的斜率为k2.若椭圆的离心率为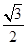 ,且过点A(0,1).
,且过点A(0,1).
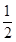 x(x+1)(41-2x)(x≤12且x∈N*)
x(x+1)(41-2x)(x≤12且x∈N*)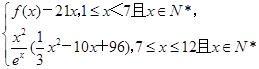
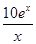 ,问:该商场销售A品牌商品,预计第几月的月利润达到最大值?月利润最大值是多少?(e6≈403)
,问:该商场销售A品牌商品,预计第几月的月利润达到最大值?月利润最大值是多少?(e6≈403)
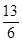 ,求sin θ+cos θ的值;
,求sin θ+cos θ的值;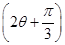 的值.
的值.