适用年级:{{getGradeNameByProperty('高三|专题试卷|全国|2014年')}} 试卷类型:{{getTestPaperTypeName('高三|专题试卷|全国|2014年')}} 使用省份:{{getAreaName('高三|专题试卷|全国|2014年')}}
试卷年份:{{getYear('高三|专题试卷|全国|2014年')}}上传日期:2014-03-17题数:11
提示:单击题文可显示答案与解析。
题号:948432
题型:选择题
难易度:较难
日期:2014-03-17
来源:2014年高考数学(理)二轮专题复习知能提升演练1-5-3练习卷(带解析)
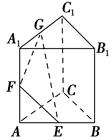
【题文】正三棱柱
ABC-
A1B1C1的棱长都为2,
E,
F,
G为
AB,
AA1,
A1C1的中点,则
B1F与平面
GEF所成角的正弦值为( ).
题号:948433
题型:选择题
难易度:一般
日期:2014-03-17
来源:2014年高考数学(理)二轮专题复习知能提升演练1-5-3练习卷(带解析)
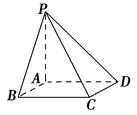
【题文】过正方形
ABCD的顶点
A,引
PA⊥平面
ABCD.若
PA=
BA,则平面
ABP和平面
CDP所成的二面角的大小是( ).
题号:948434
题型:选择题
难易度:一般
日期:2014-03-17
来源:2014年高考数学(理)二轮专题复习知能提升演练1-5-3练习卷(带解析)
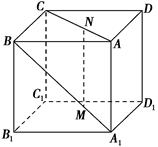
【题文】如图,在正方体
ABCD-
A1B1C1D1中,棱长为
a,
M,
N分别为
A1B和
AC上的点,
A1M=
AN=
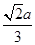
,则
MN与平面
BB1C1C的位置关系是 ( ).
题号:948435
题型:选择题
难易度:一般
日期:2014-03-17
来源:2014年高考数学(理)二轮专题复习知能提升演练1-5-3练习卷(带解析)
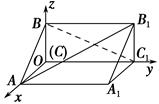
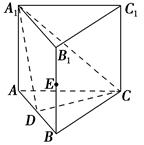
【题文】如图所示,在空间直角坐标系中有直三棱柱
ABC-
A1B1C1,
CA=
CC1=2
CB,则直线
BC1与直线
AB1夹角的余弦值为 ( ).
题号:4187737
题型:选择题
难易度:一般
日期:2014-03-21
来源:2014年高考数学(理)二轮专题复习知能提升演练1-5-3练习卷(带解析)
【题文】在正方体
ABCD-
A1B1C1D1中,
M,
N分别为棱
AA1和
BB1的中点,则sin〈
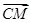
,
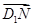
〉的值为 ( ).
题号:948410
题型:填空题
难易度:较难
日期:2014-03-17
来源:2014年高考数学(理)二轮专题复习知能提升演练1-5-3练习卷(带解析)
【题文】在正四棱锥S-ABCD中,O为顶点在底面上的射影,P为侧棱SD的中点,且SO=OD,则直线BC与平面PAC所成的角是________.
题号:948411
题型:填空题
难易度:一般
日期:2014-03-17
来源:2014年高考数学(理)二轮专题复习知能提升演练1-5-3练习卷(带解析)
【题文】在四面体P-ABC中,PA,PB,PC两两垂直,设PA=PB=PC=a,则点P到平面ABC的距离为________.
题号:4187738
题型:填空题
难易度:一般
日期:2014-03-21
来源:2014年高考数学(理)二轮专题复习知能提升演练1-5-3练习卷(带解析)
【题文】在正方体
ABCD-
A1B1C1D1中,
M,
N分别是棱
CD,
CC1的中点,则异面直线
A1M与
DN所成的角的大小是________
题号:948408
题型:解答题
难易度:较难
日期:2014-03-17
来源:2014年高考数学(理)二轮专题复习知能提升演练1-5-3练习卷(带解析)
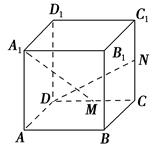
【题文】如图,在长方体
ABCD-
A1B1C1D1中,
AA1=
AD=1,
E为
CD的中点.
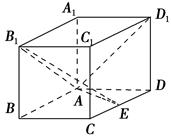
(1)求证:
B1E⊥
AD1.
(2)在棱
AA1上是否存在一点
P,使得
DP∥平面
B1AE?若存在,求
AP的长;若不存在,说明理由.
(3)若二面角
A-
B1E-
A1的大小为30°,求
AB的长.
题号:948409
题型:解答题
难易度:较难
日期:2014-03-17
来源:2014年高考数学(理)二轮专题复习知能提升演练1-5-3练习卷(带解析)
【题文】已知四边形
ABCD是菱形,∠
BAD=60°,四边形
BDEF是矩形,平面
BDEF⊥平面
ABCD,
G,
H分别是
CE,
CF的中点.
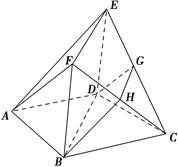
(1)求证:平面
AEF∥平面
BDGH(2)若平面
BDGH与平面
ABCD所成的角为60°,求直线
CF与平面
BDGH所成的角的正弦值.
题号:4187739
题型:解答题
难易度:较难
日期:2014-03-21
来源:2014年高考数学(理)二轮专题复习知能提升演练1-5-3练习卷(带解析)
【题文】如图,在直三棱柱
ABC-
A1B1C1中,
D,
E分别是
AB,
BB1的中点,
AA1=
AC=
CB=
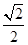 AB
AB.
(1)证明:
BC1∥平面
A1CD;
(2)求二面角
D-
A1C-
E的正弦值.

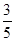
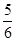
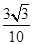
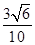

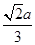 ,则MN与平面BB1C1C的位置关系是 ( ).
,则MN与平面BB1C1C的位置关系是 ( ).

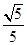
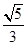
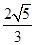
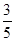
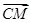 ,
,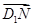 〉的值为 ( ).
〉的值为 ( ).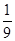
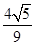
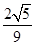
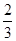



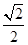 AB.
AB. 