适用年级:{{getGradeNameByProperty('高三|专题试卷|全国|2014年')}} 试卷类型:{{getTestPaperTypeName('高三|专题试卷|全国|2014年')}} 使用省份:{{getAreaName('高三|专题试卷|全国|2014年')}}
试卷年份:{{getYear('高三|专题试卷|全国|2014年')}}上传日期:2014-03-17题数:11
提示:单击题文可显示答案与解析。
题号:948577
题型:选择题
难易度:一般
日期:2014-03-17
来源:2014年高考数学(理)二轮专题复习知能提升演练1-2-2练习卷(带解析)
【题文】设函数
f(
x)=
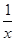
,
g(
x)=-
x2+
bx,若
y=
f(
x)的图象与
y=
g(
x)的图象有且仅有两个不同的公共点
A(
x1,
y1),
B(
x2,
y2),则下列判断正确的是 ( ).
| A.x1+x2>0,y1+y2>0 |
| B.x1+x2<0,y1+y2>0 |
| C.x1+x2>0,y1+y2<0 |
| D.x1+x2<0,y1+y2<0 |
题号:948578
题型:选择题
难易度:一般
日期:2014-03-17
来源:2014年高考数学(理)二轮专题复习知能提升演练1-2-2练习卷(带解析)
【题文】设函数
f(
x)=ln
x,
g(
x)=
x2-4
x+4,则方程
f(
x)-
g(
x)=0的实根个数是 ( ).
题号:948579
题型:选择题
难易度:较易
日期:2014-03-17
来源:2014年高考数学(理)二轮专题复习知能提升演练1-2-2练习卷(带解析)
【题文】已知函数
f(
x)=
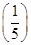 x
x-log
3x,若实数
x0是方程
f(
x)=0的解,且0<
x1<
x0,则
f(
x1)的值 ( ).
题号:4187757
题型:选择题
难易度:一般
日期:2014-03-20
来源:2014年高考数学(理)二轮专题复习知能提升演练1-2-2练习卷(带解析)
【题文】若关于
x的方程
x2+
mx+1=0有两个不相等的实数根,则实数
m的取值范围是 ( ).
| A.(-1,1) | B.(-2,2) |
| C.(-∞,-2)∪(2,+∞) | D.(-∞,-1)∪(1,+∞) |
题号:4187758
题型:选择题
难易度:一般
日期:2014-03-20
来源:2014年高考数学(理)二轮专题复习知能提升演练1-2-2练习卷(带解析)
【题文】根据统计,一名工人组装第
x件某产品所用的时间(单位:分钟)为
f(
x)=
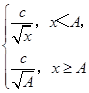
(
A,
c为常数).已知工人组装第4件产品用时30分钟,组装第
A件产品用时15分钟,那么
c和
A的值分别是 ( ).
| A.75,25 | B.75,16 | C.60,25 | D.60,16 |
题号:948575
题型:填空题
难易度:较易
日期:2014-03-17
来源:2014年高考数学(理)二轮专题复习知能提升演练1-2-2练习卷(带解析)
【题文】设a>0,b>0,e为自然对数的底数,ea+2a=eb+3b,则a与b的大小关系是________.
题号:948576
题型:填空题
难易度:较易
日期:2014-03-17
来源:2014年高考数学(理)二轮专题复习知能提升演练1-2-2练习卷(带解析)
【题文】已知0<
a<1,函数
f(
x)=
ax-|log
ax|的零点个数为________.

题号:4187759
题型:填空题
难易度:较易
日期:2014-03-20
来源:2014年高考数学(理)二轮专题复习知能提升演练1-2-2练习卷(带解析)
【题文】在如图所示的锐角三角形空地中,欲建一个面积最大的内接矩形花园(阴影部分),则其边长
x为________ m.

题号:4187637
题型:解答题
难易度:一般
日期:2014-03-22
来源:2014年高考数学(理)二轮专题复习知能提升演练1-2-2练习卷(带解析)
【题文】设函数f(x)=ax2+bx+b-1(a≠0).
(1)当a=1,b=-2时,求函数f(x)的零点;
(2)若对任意b∈R,函数f(x)恒有两个不同零点,求实数a的取值范围.
题号:4187761
题型:解答题
难易度:较难
日期:2014-03-18
来源:2014年高考数学(理)二轮专题复习知能提升演练1-2-2练习卷(带解析)
【题文】设函数
f(
x)=
x3-
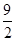 x2
x2+6
x-
a.
(1)对于任意实数
x,
f′(
x)≥
m恒成立,求
m的最大值;
(2)若方程
f(
x)=0有且仅有一个实根,求
a的取值范围.
题号:4187762
题型:解答题
难易度:较难
日期:2014-03-18
来源:2014年高考数学(理)二轮专题复习知能提升演练1-2-2练习卷(带解析)
【题文】某商场销售某种商品的经验表明,该商品每日的销售量
y(单位:千克)与销售价格
x(单位:元/千克)满足关系式
y=
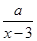
+10(
x-6)
2,其中3<
x<6,
a为常数.已知销售价格为5元/千克时,每日可售出该商品11千克.
(1)求
a的值;
(2)若该商品的成本为3元/千克,试确定销售价格
x的值,使商场每日销售该商品所获得的利润最大.
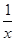 ,g(x)=-x2+bx,若y=f(x)的图象与y=g(x)的图象有且仅有两个不同的公共点A(x1,y1),B(x2,y2),则下列判断正确的是 ( ).
,g(x)=-x2+bx,若y=f(x)的图象与y=g(x)的图象有且仅有两个不同的公共点A(x1,y1),B(x2,y2),则下列判断正确的是 ( ).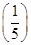 x-log3x,若实数x0是方程f(x)=0的解,且0<x1<x0,则f(x1)的值 ( ).
x-log3x,若实数x0是方程f(x)=0的解,且0<x1<x0,则f(x1)的值 ( ).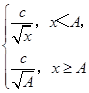 (A,c为常数).已知工人组装第4件产品用时30分钟,组装第A件产品用时15分钟,那么c和A的值分别是 ( ).
(A,c为常数).已知工人组装第4件产品用时30分钟,组装第A件产品用时15分钟,那么c和A的值分别是 ( ).

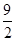 x2+6x-a.
x2+6x-a.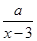 +10(x-6)2,其中3<x<6,a为常数.已知销售价格为5元/千克时,每日可售出该商品11千克.
+10(x-6)2,其中3<x<6,a为常数.已知销售价格为5元/千克时,每日可售出该商品11千克.