适用年级:{{getGradeNameByProperty('高三|专题试卷|全国|2014年')}} 试卷类型:{{getTestPaperTypeName('高三|专题试卷|全国|2014年')}} 使用省份:{{getAreaName('高三|专题试卷|全国|2014年')}}
试卷年份:{{getYear('高三|专题试卷|全国|2014年')}}上传日期:2014-03-16题数:11
提示:单击题文可显示答案与解析。
题号:948792
题型:选择题
难易度:一般
日期:2014-03-16
来源:2014年高考数学(理)二轮复习专题提升训练训练16练习卷(带解析)
【题文】过抛物线
y2=2
px(
p>0)的焦点
F且倾斜角为60°的直线
l与抛物线分别交于
A,
B两点,则
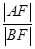
的值等于( ).
题号:948793
题型:选择题
难易度:一般
日期:2014-03-16
来源:2014年高考数学(理)二轮复习专题提升训练训练16练习卷(带解析)
【题文】已知椭圆
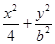
=1(0<
b<2)与
y轴交于
A,
B两点,点
F为该椭圆的一个焦点,则△
ABF面积的最大值为( ).
题号:948794
题型:选择题
难易度:一般
日期:2014-03-16
来源:2014年高考数学(理)二轮复习专题提升训练训练16练习卷(带解析)
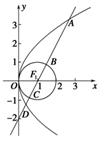
【题文】已知抛物线
y2=4
x,圆
F:(
x-1)
2+
y2=1,过点
F作直线
l,自上而下顺次与上述两曲线交于点
A,
B,
C,
D(如图所示),则|
AB|·|
CD|的值正确的是( ).
题号:948795
题型:选择题
难易度:一般
日期:2014-03-16
来源:2014年高考数学(理)二轮复习专题提升训练训练16练习卷(带解析)
【题文】若双曲线
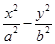
=1(
a>0,
b>0)与直线
y=
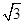 x
x无交点,则离心率
e的取值范围是( ).
| A.(1,2) | B.(1,2] | C.(1,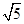 ) ) | D.(1,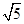 ] ] |
题号:4187826
题型:选择题
难易度:较易
日期:2014-03-17
来源:2014年高考数学(理)二轮复习专题提升训练训练16练习卷(带解析)
【题文】直线4
kx-4
y-
k=0与抛物线
y2=
x交于
A,
B两点,若|
AB|=4,则弦
AB的中点到直线
x+
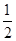
=0的距离等于( ).
A.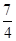 | B.2 | C.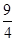 | D.4 |
题号:4187827
题型:填空题
难易度:较易
日期:2014-03-20
来源:2014年高考数学(理)二轮复习专题提升训练训练16练习卷(带解析)
【题文】抛物线
x2=2
py(
p>0)的焦点为
F,其准线与双曲线
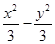
=1相交于
A,
B两点,若△
ABF为等边三角形,则
p=________.
题号:4187828
题型:填空题
难易度:一般
日期:2014-03-20
来源:2014年高考数学(理)二轮复习专题提升训练训练16练习卷(带解析)
【题文】已知点
F是双曲线
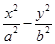
=1(
a>0,
b>0)的左焦点,点
E是该双曲线的右顶点,过点
F且垂直于
x轴的直线与双曲线交于
A,
B两点,若△
ABE是锐角三角形,则该双曲线的离心率
e的取值范围是________.
题号:4187829
题型:填空题
难易度:较难
日期:2014-03-20
来源:2014年高考数学(理)二轮复习专题提升训练训练16练习卷(带解析)
【题文】设
F1是椭圆
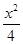
+
y2=1的左焦点,
O为坐标原点,点
P在椭圆上,则
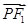
·
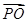
的最大值为________.
题号:4187622
题型:解答题
难易度:较难
日期:2014-03-23
来源:2014年高考数学(理)二轮复习专题提升训练训练16练习卷(带解析)
【题文】已知椭圆的焦点坐标为F1(-1,0),F2(1,0),过F2垂直于长轴的直线交椭圆于P,Q两点,且|PQ|=3.
(1)求椭圆的方程;
(2)过F2的直线l与椭圆交于不同的两点M,N,则△F1MN的内切圆的面积是否存在最大值?若存在,求出这个最大值及此时的直线方程;若不存在,请说明理由.
题号:4187830
题型:解答题
难易度:较难
日期:2014-03-20
来源:2014年高考数学(理)二轮复习专题提升训练训练16练习卷(带解析)
【题文】已知
A,
B,
C是椭圆
W:
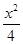
+
y2=1上的三个点,
O是坐标原点.
(1)当点
B是
W的右顶点,且四边形
OABC为菱形时,求此菱形的面积;
(2)当点
B不是
W的顶点时,判断四边形
OABC是否可能为菱形,并说明理由.
题号:4187831
题型:解答题
难易度:较难
日期:2014-03-20
来源:2014年高考数学(理)二轮复习专题提升训练训练16练习卷(带解析)
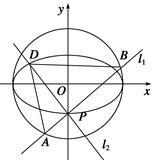
【题文】如图,点
P(0,-1)是椭圆
C1:
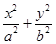
=1(
a>
b>0)的一个顶点,
C1的长轴是圆
C2:
x2+
y2=4的直径.
l1,
l2是过点
P且互相垂直的两条直线,其中
l1交圆
C2于
A,
B两点,
l2交椭圆
C1于另一点
D.
(1)求椭圆
C1的方程;
(2)求△
ABD面积取最大值时直线
l1的方程.
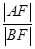 的值等于( ).
的值等于( ).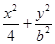 =1(0<b<2)与y轴交于A,B两点,点F为该椭圆的一个焦点,则△ABF面积的最大值为( ).
=1(0<b<2)与y轴交于A,B两点,点F为该椭圆的一个焦点,则△ABF面积的最大值为( ).
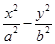 =1(a>0,b>0)与直线y=
=1(a>0,b>0)与直线y=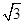 x无交点,则离心率e的取值范围是( ).
x无交点,则离心率e的取值范围是( ).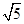 )
)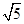 ]
]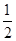 =0的距离等于( ).
=0的距离等于( ).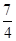
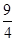
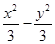 =1相交于A,B两点,若△ABF为等边三角形,则p=________.
=1相交于A,B两点,若△ABF为等边三角形,则p=________.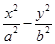 =1(a>0,b>0)的左焦点,点E是该双曲线的右顶点,过点F且垂直于x轴的直线与双曲线交于A,B两点,若△ABE是锐角三角形,则该双曲线的离心率e的取值范围是________.
=1(a>0,b>0)的左焦点,点E是该双曲线的右顶点,过点F且垂直于x轴的直线与双曲线交于A,B两点,若△ABE是锐角三角形,则该双曲线的离心率e的取值范围是________.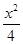 +y2=1的左焦点,O为坐标原点,点P在椭圆上,则
+y2=1的左焦点,O为坐标原点,点P在椭圆上,则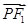 ·
·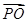 的最大值为________.
的最大值为________. 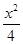 +y2=1上的三个点,O是坐标原点.
+y2=1上的三个点,O是坐标原点.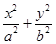 =1(a>b>0)的一个顶点,C1的长轴是圆C2:x2+y2=4的直径.l1,l2是过点P且互相垂直的两条直线,其中l1交圆C2于A,B两点,l2交椭圆C1于另一点D.
=1(a>b>0)的一个顶点,C1的长轴是圆C2:x2+y2=4的直径.l1,l2是过点P且互相垂直的两条直线,其中l1交圆C2于A,B两点,l2交椭圆C1于另一点D.