适用年级:{{getGradeNameByProperty('高三|专题试卷|全国|2014年')}} 试卷类型:{{getTestPaperTypeName('高三|专题试卷|全国|2014年')}} 使用省份:{{getAreaName('高三|专题试卷|全国|2014年')}}
试卷年份:{{getYear('高三|专题试卷|全国|2014年')}}上传日期:2014-03-16题数:11
提示:单击题文可显示答案与解析。
题号:948802
题型:选择题
难易度:一般
日期:2014-03-16
来源:2014年高考数学(理)二轮复习专题提升训练训练14练习卷(带解析)
【题文】直线
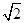 ax
ax+
by=1与圆
x2+
y2=1相交于
A,
B两点(其中
a,
b是实数),且△
AOB是直角三角形(
O是坐标原点),则点
P(
a,
b)与点(0,1)之间距离的最小值为( ).
题号:948803
题型:选择题
难易度:一般
日期:2014-03-16
来源:2014年高考数学(理)二轮复习专题提升训练训练14练习卷(带解析)
【题文】“
a=
b”是“直线
y=
x+2与圆(
x-
a)
2+(
x-
b)
2=2相切”的( ).
| A.充分不必要条件 | B.必要不充分条件 |
| C.充要条件 | D.既不充分也不必要条件 |
题号:948804
题型:选择题
难易度:容易
日期:2014-03-16
来源:2014年高考数学(理)二轮复习专题提升训练训练14练习卷(带解析)
【题文】已知倾斜角为
α的直线
l与直线
x-2
y+2=0平行,则tan 2
α的值为( ).
题号:4187840
题型:选择题
难易度:较易
日期:2014-03-17
来源:2014年高考数学(理)二轮复习专题提升训练训练14练习卷(带解析)
【题文】已知圆(
x-
a)
2+(
y-
b)
2=
r2的圆心为抛物线
y2=4
x的焦点,且与直线3
x+4
y+2=0相切,则该圆的方程为( ).
A.(x-1)2+y2=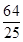 | B.x2+(y-1)2=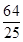 |
| C.(x-1)2+y2=1 | D.x2+(y-1)2=1 |
题号:4187841
题型:选择题
难易度:一般
日期:2014-03-17
来源:2014年高考数学(理)二轮复习专题提升训练训练14练习卷(带解析)
【题文】已知圆的方程为
x2+
y2-6
x-8
y=0,设该圆中过点(3,5)的最长弦和最短弦分别为
AC和
BD,则四边形
ABCD的面积是( ).
题号:948801
题型:填空题
难易度:一般
日期:2014-03-16
来源:2014年高考数学(理)二轮复习专题提升训练训练14练习卷(带解析)
【题文】若直线l:4x+3y-8=0过圆C:x2+y2-ax=0的圆心且交圆C于A,B两点,O坐标原点,则△OAB的面积为________.
题号:4187733
题型:填空题
难易度:较易
日期:2014-03-21
来源:2014年高考数学(理)二轮复习专题提升训练训练14练习卷(带解析)
【题文】设圆x2+y2=2的切线l与x轴的正半轴、y轴的正半轴分别交于点A,B,当|AB|取最小值时,切线l的方程为________.
题号:4187842
题型:填空题
难易度:一般
日期:2014-03-17
来源:2014年高考数学(理)二轮复习专题提升训练训练14练习卷(带解析)
【题文】若圆
x2+
y2=4与圆
x2+
y2+2
ax-6=0(
a>0)的公共弦的长为2
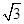
,则
a=________.
题号:789363
题型:解答题
难易度:一般
日期:2016-01-18
来源:2014年高考数学(理)二轮复习专题提升训练训练14练习卷(带解析)
【题文】在平面直角坐标系xOy中,曲线y=x2-6x+1与坐标轴的交点都在圆C上.
(1)求圆C的方程;
(2)若圆C与直线x-y+a=0交于A,B两点,且OA⊥OB,求a的值.
题号:4187844
题型:解答题
难易度:较难
日期:2014-03-17
来源:2014年高考数学(理)二轮复习专题提升训练训练14练习卷(带解析)
【题文】已知点A(-3,0),B(3,0),动点P满足|PA|=2|PB|.
(1)若点P的轨迹为曲线C,求此曲线的方程;
(2)若点Q在直线l1:x+y+3=0上,直线l2经过点Q且与曲线C只有一个公共点M,求|QM|的最小值.
题号:4187845
题型:解答题
难易度:较难
日期:2014-03-17
来源:2014年高考数学(理)二轮复习专题提升训练训练14练习卷(带解析)
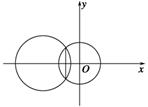
【题文】已知以点
C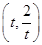
(
t∈R,
t≠0)为圆心的圆与
x轴交于点
O,
A,与
y轴交于点
O,
B,其中
O为原点.
(1)求证:△
AOB的面积为定值;
(2)设直线2
x+
y-4=0与圆
C交于点
M,
N,若|
OM|=|
ON|,求圆
C的方程;
(3)在(2)的条件下,设
P,
Q分别是直线
l:
x+
y+2=0和圆
C上的动点,求|
PB|+|
PQ|的最小值及此时点
P的坐标.
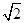 ax+by=1与圆x2+y2=1相交于A,B两点(其中a,b是实数),且△AOB是直角三角形(O是坐标原点),则点P(a,b)与点(0,1)之间距离的最小值为( ).
ax+by=1与圆x2+y2=1相交于A,B两点(其中a,b是实数),且△AOB是直角三角形(O是坐标原点),则点P(a,b)与点(0,1)之间距离的最小值为( ).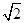
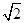 -1
-1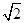 +1
+1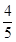
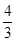
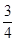
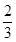
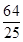
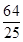
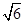
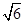
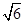
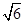
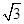 ,则a=________.
,则a=________.
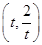 (t∈R,t≠0)为圆心的圆与x轴交于点O,A,与y轴交于点O,B,其中O为原点.
(t∈R,t≠0)为圆心的圆与x轴交于点O,A,与y轴交于点O,B,其中O为原点.