适用年级:{{getGradeNameByProperty('高三|专题试卷|全国|2010年')}} 试卷类型:{{getTestPaperTypeName('高三|专题试卷|全国|2010年')}} 使用省份:{{getAreaName('高三|专题试卷|全国|2010年')}}
试卷年份:{{getYear('高三|专题试卷|全国|2010年')}}上传日期:2010-06-25题数:38
提示:单击题文可显示答案与解析。
题号:1261284
题型:选择题
难易度:一般
日期:2010-06-17
来源:2010年高考试题分项版理科数学之专题八 圆锥曲线
【题文】已知椭圆
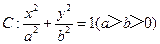
的离心率为
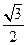
,过右焦点
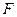
且斜率为
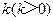
的直线与
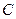
相交于
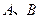
两点.若
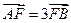
,则
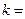
| A.1 | B.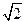 | C.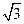 | D.2 |
题号:1262583
题型:选择题
难易度:一般
日期:2010-06-15
来源:2010年高考试题分项版理科数学之专题八 圆锥曲线
【题文】设双曲线的一个焦点为
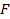
,虚轴的一个端点为
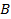
,如果直线
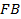
与该双曲线的一条渐近线垂直,那么此双曲线的离心率为( )
题号:1263928
题型:选择题
难易度:较易
日期:2010-06-09
来源:2010年高考试题分项版理科数学之专题八 圆锥曲线
【题文】已知抛物线
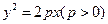
的准线与圆

相切,则p的值为【】
A.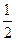 | B.1 | C.2 | D.4 |
题号:1264244
题型:选择题
难易度:较难
日期:2010-06-08
来源:2010年高考试题分项版理科数学之专题八 圆锥曲线
【题文】双曲线方程为
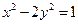
,则它的右焦点坐标为
题号:3411192
题型:选择题
难易度:较难
日期:2010-06-23
来源:2010年高考试题分项版理科数学之专题八 圆锥曲线
【题文】已知
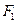
、
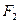
为双曲线C:
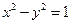
的左、右焦点,点
P在
C上,∠
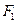 P
P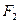
=
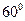
,则
P到
x轴的距离为
题号:3428548
题型:选择题
难易度:一般
日期:2012-07-17
来源:2010年高考试题分项版理科数学之专题八 圆锥曲线
【题文】设抛物线y
2=8x的焦点为F,准线为l,P为抛物线上一点,PA⊥l,A为垂足.如
果直线AF的斜率为
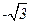
,那么|PF|=
A.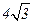 | B.8 | C.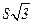 | D.16 |
题号:3600858
题型:选择题
难易度:一般
日期:2012-07-02
来源:2010年高考试题分项版理科数学之专题八 圆锥曲线
【题文】已知双曲线
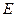
的中心为原点,
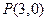
是
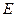
的焦点,过F的直线
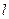
与
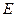
相交于A,B两点,且AB的中点为
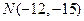
,则
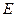
的方程式为
题号:3603244
题型:选择题
难易度:一般
日期:2010-06-18
来源:2010年高考试题分项版理科数学之专题八 圆锥曲线
【题文】半径为
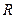
的球
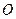
的直径
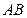
垂直于平面
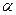
,垂足为
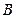
,
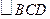
是平面
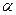
内边长为
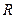
的正三角形,线段
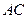
、
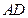
分别
与球面交于点
M,
N,那么
M、
N两点间的球面距离是
(
A)

(
B)
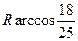
(
C)
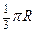
(
D)
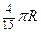
题号:3759108
题型:选择题
难易度:一般
日期:2012-07-05
来源:2010年高考试题分项版理科数学之专题八 圆锥曲线
【题文】已知双曲线
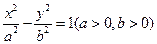
的一条渐近线方程是y=
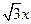
,它的一个焦点在抛物线
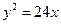
的准线上,则双曲线的方程为
题号:3766548
题型:选择题
难易度:较易
日期:2010-06-10
来源:2010年高考试题分项版理科数学之专题八 圆锥曲线
【题文】以抛物线y
2=4x的焦点为圆心,且过坐标原点的圆的方程为
| A.x2+y2+2x="0" | B.x2+y2+x=0 |
| C.x2+y2-x="0" | D.x2+y2-2x=0 |
题号:3766554
题型:选择题
难易度:较易
日期:2010-06-10
来源:2010年高考试题分项版理科数学之专题八 圆锥曲线
题号:4217134
题型:选择题
难易度:一般
日期:2012-07-04
来源:2010年高考试题分项版理科数学之专题八 圆锥曲线
【题文】
设
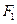
、
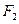
分别为双曲线
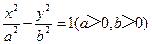
的左、右焦点.若在双曲线右支上存在点
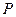
,满足
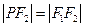
,且
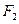
到直线
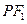
的距离等于双曲线的实轴长,则该双曲线的渐近线方程为
题号:1261161
题型:填空题
难易度:一般
日期:2010-06-17
来源:2010年高考试题分项版理科数学之专题八 圆锥曲线
【题文】已知抛物线
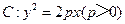
的准线为
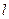
,过
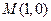
且斜率为
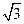
的直线与
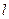
相交于点
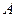
,与
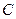
的一个交点为
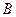
.若
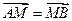
,则
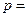
.
题号:1261624
题型:填空题
难易度:一般
日期:2010-06-17
来源:2010年高考试题分项版理科数学之专题八 圆锥曲线
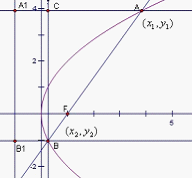
【题文】已知以F为焦点的抛物线
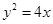
上的两点A、B满足
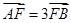
,则弦AB的中点到准线的距离为___________.
题号:1261826
题型:填空题
难易度:一般
日期:2010-06-15
来源:2010年高考试题分项版理科数学之专题八 圆锥曲线
【题文】
点

在双曲线

的右支上,若点

到右焦点的距离等于
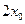
,则
 .
.
题号:1264380
题型:填空题
难易度:较难
日期:2010-06-08
来源:2010年高考试题分项版理科数学之专题八 圆锥曲线
【题文】在平面直角坐标系xOy中,双曲线
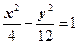
上一点M,点M的横坐标是3,则M到双曲线右焦点的距离是___
_______
题号:3411195
题型:填空题
难易度:较难
日期:2013-04-02
来源:2010年高考试题分项版理科数学之专题八 圆锥曲线
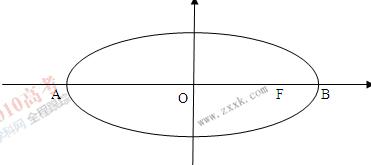
【题文】已知
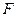
是椭圆
C的一个焦点,
B是短轴的一个端点,线段
BF的延长线交
C于点
D,且
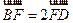
,则
C的离心率为
.
题号:3760205
题型:填空题
难易度:较难
日期:2013-04-11
来源:2010年高考试题分项版理科数学之专题八 圆锥曲线
【题文】已知双曲线

的离心率为2,焦点与椭圆
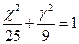
的焦点相同,那么双曲线的焦点坐标为
;渐近线方程为
。
题号:3877103
题型:填空题
难易度:较易
日期:2012-08-07
来源:2010年高考试题分项版理科数学之专题八 圆锥曲线
【题文】过抛物线
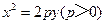
的焦点作斜率为1的直线与该抛物线交于

两点,

在
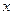
轴上的正射影分别为

.若梯形
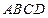
的面积为
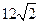
,则

.
题号:4217135
题型:填空题
难易度:一般
日期:2013-01-05
来源:2010年高考试题分项版理科数学之专题八 圆锥曲线
【题文】
设抛物线
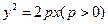
的焦点为
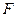
,点
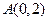
.若线段
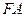
的中点
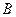
在抛物线上,则
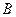
到该抛物线准线的距离为_____________。
题号:1084987
题型:解答题
难易度:一般
日期:2012-05-05
来源:2010年高考试题分项版理科数学之专题八 圆锥曲线
【题文】已知一条曲线C在y轴右边,C上每一点到点F(1,0)的距离减去它到y轴距离的差都是1
(1)求曲线C的方程.
(2)是否存在正数m,对于过点M(m,0)且与曲线C有两个交点A,B的任一直线,都有

?若存在,求出m的取值范围,若不存在,请说明理由.
题号:1258279
题型:解答题
难易度:较难
日期:2010-06-23
来源:2010年高考试题分项版理科数学之专题八 圆锥曲线
【题文】已知抛物线
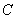
:

的焦点为

,过点

的直线

与
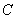
相交于

、

两点,点

关于

轴的对称点为

.
(Ⅰ)判断点

是否在直线

上,并给出证明;
(Ⅱ)设
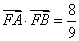
,求

的内切圆
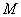
的方程.
题号:1261157
题型:解答题
难易度:一般
日期:2010-06-17
来源:2010年高考试题分项版理科数学之专题八 圆锥曲线
【题文】己知斜率为1的直线
l与双曲线
C:
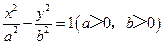
相交于
B、
D两点,且
BD的中点为
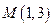
.
(Ⅰ)求
C的离心率;
(Ⅱ)设
C的右顶点为
A,右焦点为
F,
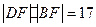
,证明:过
A、
B、
D三点的圆与
x轴相切.
题号:1261499
题型:解答题
难易度:一般
日期:2010-06-17
来源:2010年高考试题分项版理科数学之专题八 圆锥曲线
【题文】已知以原点O为中心,
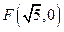
为右焦点的双曲线C的离心率
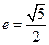
。
(I) 求双曲线C的标准方程及其渐近线方程;
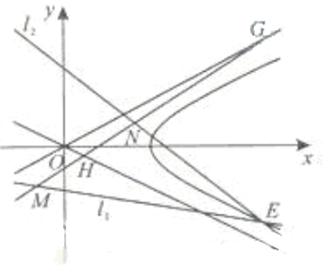
(II) 如题(20)图,已知过点
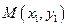
的直线
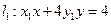
与过点
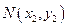
(其中
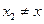
)的直线
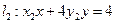
的交点E在双曲线C上,直线MN与两条渐近线分别交与G、H两点,求
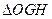
的面积。
题号:1261642
题型:解答题
难易度:一般
日期:2010-06-15
来源:2010年高考试题分项版理科数学之专题八 圆锥曲线
【题文】

设椭圆

:
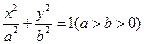
,抛物线

:

.
(1) 若

经过

的两个焦点,求

的离心率;
(2) 设
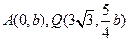
,又
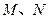
为

与

不在
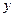
轴上的两个交点,若
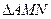
的垂心为
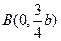
,且

的重心在

上,求椭圆

和抛物线

的方程.
题号:1262765
题型:解答题
难易度:一般
日期:2010-06-13
来源:2010年高考试题分项版理科数学之专题八 圆锥曲线
【题文】设
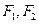
分别是椭圆
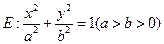
的左、右焦点,过
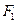
斜率为1的直线
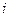
与
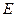
相交于
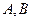
两点,且
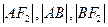
成等差数列。
(1)求
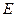
的离心率;
(2)设点
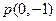
满足
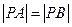
,求
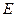
的方程
题号:1263604
题型:解答题
难易度:一般
日期:2010-06-10
来源:2010年高考试题分项版理科数学之专题八 圆锥曲线
【题文】一条双曲线

的左、右顶点分别为A
1,A
2,点

,
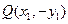
是双曲线上不同的两个动点。
(1)求直线A
1P与A
2Q交点的轨迹E的方程式;
(2)若过点H(0, h)(h>1)的两条直线l
1和l
2与轨迹E都只有一个交点,且
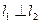 ,
,求h的值。
题号:1263768
题型:解答题
难易度:较易
日期:2010-06-09
来源:2010年高考试题分项版理科数学之专题八 圆锥曲线
【题文】(本小题满分13分)
为了考察冰川的融化状况,一支科考队在某冰川上相距8km的A,B两点各建一个考察基地。视冰川面为平面形,以过A,B两点的直线为x轴,线段AB的的垂直平分线为y轴建立平面直角坐标系(图6)在直线x=2的右侧,考察范围为到点B的距离不超过
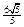
km区域;在直线x=2的左侧,考察范围为到A,B两点的距离之和不超过
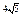
km区域。
(Ⅰ)求考察区域边界曲线的方程;
(Ⅱ)如图6所示,设线段P
1P
2,P
2P
3是冰川的部分边界线(不考虑其他边界线),当冰川融化时,边界线沿与其垂直的方向朝考察区域平行移动,第一年移动0.2km,以后每年移动的距离为前一年的2倍,求冰川边界线移动到考察区域所需的最短时间。

题号:1263921
题型:解答题
难易度:较易
日期:2010-06-09
来源:2010年高考试题分项版理科数学之专题八 圆锥曲线
【题文】

题号:1264251
题型:解答题
难易度:较难
日期:2010-06-08
来源:2010年高考试题分项版理科数学之专题八 圆锥曲线
【题文】(16分)在平面直角坐标系
中,如图,已知椭圆
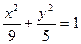
的左右顶点为A,B,右顶点为F,设过点T(
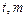
)的直线TA,TB与椭圆分别交于点M
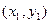
,
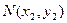
,其中m>0,
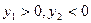
①设动点P满足
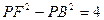
,求点P的轨迹
②设
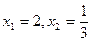
,求点T的坐标
③设
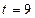
,求证:直线MN必过x轴上的一定点
(其坐标与m无关)
题号:3428554
题型:解答题
难易度:一般
日期:2013-03-25
来源:2010年高考试题分项版理科数学之专题八 圆锥曲线
【题文】设椭圆C:
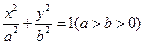
的左焦点为F,过点F的直线与椭圆C相交于A,B两点,直线l的倾斜角为60
o,
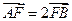
.
(I) 求椭圆C的离心率;
(II) 如果|AB|=
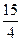
,求椭圆C的方程.
题号:3440071
题型:解答题
难易度:一般
日期:2010-06-18
来源:2010年高考试题分项版理科数学之专题八 圆锥曲线
【题文】已知定点
A(-1,0),
F(2,0),定直线
l:
x=
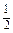
,不在
x轴上的动点
P与点
F的距离是它到直线
l的距离的2倍.设点
P的轨迹为
E,过点
F的直线交
E于
B、
C两点,直线
AB、
AC分别交
l于点
M、
N(Ⅰ)求
E的方程;
(Ⅱ)试判断以线段
MN为直径的圆是否过点
F,并说明理由.



w_w w. k#s5_u.c o*m
题号:3759111
题型:解答题
难易度:一般
日期:2010-06-13
来源:2010年高考试题分项版理科数学之专题八 圆锥曲线
【题文】已知椭圆
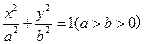
的离心率
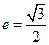
,连接椭圆的四个顶点得到的菱形的面积为4。
(1) 求椭圆的方程;
(2) 设直线
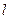
与椭圆相交于不同的两点
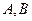
,已知点
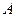
的坐标为(
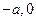
),点
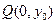
在线段
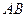
的垂直平分线上,且
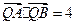
,求
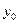
的值
题号:3760207
题型:解答题
难易度:一般
日期:2013-03-14
来源:2010年高考试题分项版理科数学之专题八 圆锥曲线
【题文】(本小题共14分)
在平面直角坐标系xOy中,点B与点A(-1,1)关于原点O对称,P是动点,且直线AP与BP的斜率之积等于

.
(Ⅰ)求动点P的轨迹方程;
(Ⅱ)设直线AP和BP分别与直线x=3交于点M,N,问:是否存在点P使得△PAB与△PMN的面积相等?

若存在,求出点P的坐标;若不存在,说明理由。
题号:3766552
题型:解答题
难易度:较易
日期:2010-06-10
来源:2010年高考试题分项版理科数学之专题八 圆锥曲线
【题文】(本小题满分13分)
已知中心在坐标原点O的椭圆C经过点A(2,3),且点F(2.0)为其右焦点。
(Ⅰ)求椭圆C的方程;
(Ⅱ)是否存在平行于OA的直线L,使得直线L与椭圆C有公共点,且直线OA与L的距离等于4?若存在,求出直线L的方程;若不存在,说明理由。
题号:3876923
题型:解答题
难易度:较难
日期:2012-05-25
来源:2010年高考试题分项版理科数学之专题八 圆锥曲线
【题文】(本小题满分13分)
已知椭圆
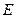
经过点
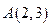
,对称轴为

坐标轴,焦点
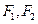
在
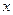
轴上,离心率
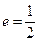
。[来源:学科网ZXXK]
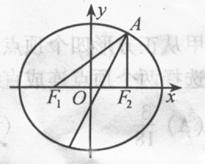
(Ⅰ)求椭圆
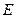
的方程;
(Ⅱ)求
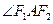
的角平分线所在直线
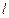
的方程;
(Ⅲ)在椭圆
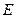
上是否存在关于直线

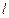
对称的相异两点?若存在,请找出;若不存在,说明理由。
题号:4217133
题型:解答题
难易度:较易
日期:2012-10-16
来源:2010年高考试题分项版理科数学之专题八 圆锥曲线
【题文】(本小题满分12分)
如图,已知椭圆
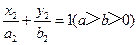
的离心率为
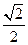
,以该椭圆上的点和椭圆的左、右焦点
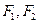
为顶点的三角形的周长为
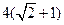
.一等轴双曲线的顶点是该椭圆的焦点,设
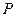
为该双曲线上异于顶点的任一点,直线
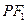
和
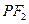
与椭圆的交点分别为
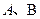
和
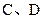
.
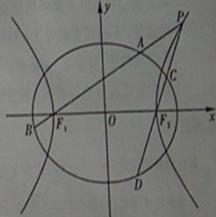
(Ⅰ)求椭圆和双曲线的标准方程;
(Ⅱ)设直线
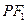
、
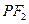
的斜率分别为
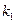
、
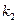
,证明
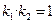
;
(Ⅲ)是否存在常数
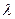
,使得
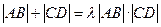
恒成立?若存在,求
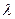
的值;若不存在,请说明理由.
题号:4217136
题型:解答题
难易度:一般
日期:2010-06-15
来源:2010年高考试题分项版理科数学之专题八 圆锥曲线
【题文】
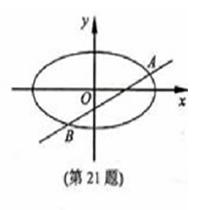
(本题满分15分)已知
m>1,直线
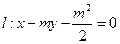
,
椭圆
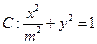
,
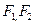
分别为椭圆
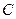
的左、右焦点.
(Ⅰ)当直线
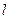
过右焦点
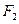
时,求直线
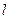
的方程;
(Ⅱ)设直线
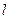
与椭圆
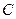
交于
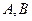
两点,
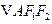
,
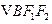
的重心分别为
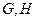
.若原点
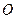
在以线段
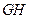
为直径的圆内,求实数
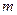
的取值范围.
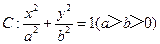 的离心率为
的离心率为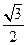 ,过右焦点
,过右焦点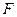 且斜率为
且斜率为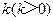 的直线与
的直线与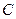 相交于
相交于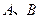 两点.若
两点.若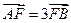 ,则
,则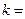
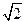
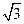
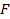 ,虚轴的一个端点为
,虚轴的一个端点为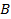 ,如果直线
,如果直线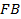 与该双曲线的一条渐近线垂直,那么此双曲线的离心率为( )
与该双曲线的一条渐近线垂直,那么此双曲线的离心率为( )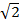
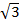
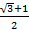
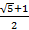
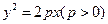 的准线与圆
的准线与圆 相切,则p的值为【】
相切,则p的值为【】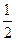
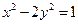 ,则它的右焦点坐标为
,则它的右焦点坐标为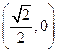
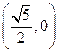
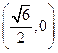
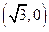
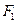 、
、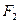 为双曲线C:
为双曲线C: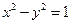 的左、右焦点,点P在C上,∠
的左、右焦点,点P在C上,∠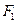 P
P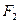 =
=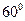 ,则P到x轴的距离为
,则P到x轴的距离为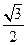
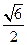
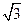
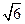
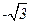 ,那么|PF|=
,那么|PF|=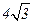
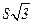
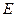 的中心为原点,
的中心为原点,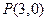 是
是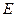 的焦点,过F的直线
的焦点,过F的直线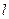 与
与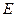 相交于A,B两点,且AB的中点为
相交于A,B两点,且AB的中点为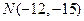 ,则
,则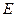 的方程式为
的方程式为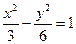
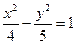
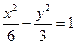
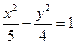
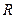 的球
的球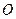 的直径
的直径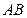 垂直于平面
垂直于平面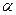 ,垂足为
,垂足为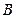 ,
,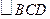 是平面
是平面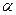 内边长为
内边长为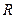 的正三角形,线段
的正三角形,线段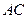 、
、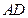 分别
分别 (B)
(B)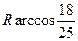
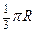 (D)
(D)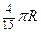
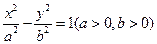 的一条渐近线方程是y=
的一条渐近线方程是y=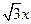 ,它的一个焦点在抛物线
,它的一个焦点在抛物线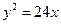 的准线上,则双曲线的方程为
的准线上,则双曲线的方程为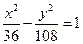
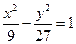

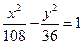
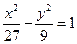
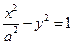 (a>0)的中心和左
(a>0)的中心和左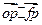 的取值范围为
的取值范围为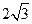 ,
,  )
)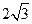 ,
,  )
) ,
,  )
)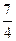 ,
,  )
)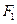 、
、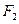 分别为双曲线
分别为双曲线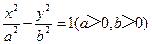 的左、右焦点.若在双曲线右支上存在点
的左、右焦点.若在双曲线右支上存在点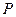 ,满足
,满足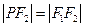 ,且
,且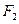 到直线
到直线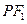 的距离等于双曲线的实轴长,则该双曲线的渐近线方程为
的距离等于双曲线的实轴长,则该双曲线的渐近线方程为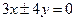
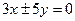
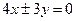
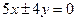
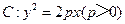 的准线为
的准线为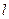 ,过
,过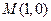 且斜率为
且斜率为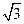 的直线与
的直线与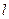 相交于点
相交于点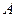 ,与
,与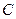 的一个交点为
的一个交点为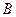 .若
.若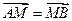 ,则
,则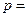 .
.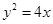 上的两点A、B满足
上的两点A、B满足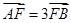 ,则弦AB的中点到准线的距离为___________.
,则弦AB的中点到准线的距离为___________.
 在双曲线
在双曲线 的右支上,若点
的右支上,若点 到右焦点的距离等于
到右焦点的距离等于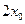 ,则
,则 .
.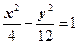 上一点M,点M的横坐标是3,则M到双曲线右焦点的距离是__________
上一点M,点M的横坐标是3,则M到双曲线右焦点的距离是__________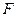 是椭圆C的一个焦点,B是短轴的一个端点,线段BF的延长线交C于点D,且
是椭圆C的一个焦点,B是短轴的一个端点,线段BF的延长线交C于点D,且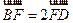 ,则C的离心率为 .
,则C的离心率为 . 的离心率为2,焦点与椭圆
的离心率为2,焦点与椭圆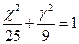 的焦点相同,那么双曲线的焦点坐标为 ;渐近线方程为 。
的焦点相同,那么双曲线的焦点坐标为 ;渐近线方程为 。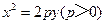 的焦点作斜率为1的直线与该抛物线交于
的焦点作斜率为1的直线与该抛物线交于 两点,
两点, 在
在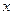 轴上的正射影分别为
轴上的正射影分别为 .若梯形
.若梯形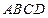 的面积为
的面积为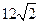 ,则
,则 .
.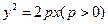 的焦点为
的焦点为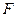 ,点
,点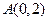 .若线段
.若线段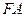 的中点
的中点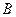 在抛物线上,则
在抛物线上,则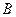 到该抛物线准线的距离为_____________。
到该抛物线准线的距离为_____________。 ?若存在,求出m的取值范围,若不存在,请说明理由.
?若存在,求出m的取值范围,若不存在,请说明理由.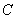 :
: 的焦点为
的焦点为 ,过点
,过点 的直线
的直线 与
与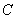 相交于
相交于 、
、 两点,点
两点,点 关于
关于 轴的对称点为
轴的对称点为 .
. 是否在直线
是否在直线 上,并给出证明;
上,并给出证明;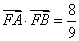 ,求
,求 的内切圆
的内切圆 的方程.
的方程.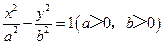 相交于B、D两点,且BD的中点为
相交于B、D两点,且BD的中点为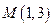 .
.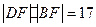 ,证明:过A、B、D三点的圆与x轴相切.
,证明:过A、B、D三点的圆与x轴相切.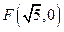 为右焦点的双曲线C的离心率
为右焦点的双曲线C的离心率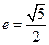 。
。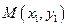 的直线
的直线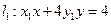 与过点
与过点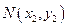 (其中
(其中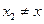 )的直线
)的直线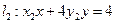 的交点E在双曲线C上,直线MN与两条渐近线分别交与G、H两点,求
的交点E在双曲线C上,直线MN与两条渐近线分别交与G、H两点,求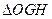 的面积。
的面积。

 :
: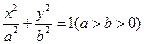 ,抛物线
,抛物线 :
: .
. 经过
经过 的两个焦点,求
的两个焦点,求 的离心率;
的离心率;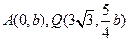 ,又
,又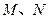 为
为 与
与 不在
不在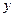 轴上的两个交点,若
轴上的两个交点,若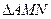 的垂心为
的垂心为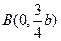 ,且
,且 的重心在
的重心在 上,求椭圆
上,求椭圆 和抛物线
和抛物线 的方程.
的方程.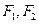 分别是椭圆
分别是椭圆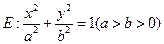 的左、右焦点,过
的左、右焦点,过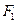 斜率为1的直线
斜率为1的直线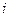 与
与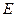 相交于
相交于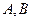 两点,且
两点,且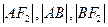 成等差数列。
成等差数列。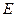 的离心率;
的离心率;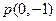 满足
满足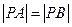 ,求
,求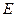 的方程
的方程 的左、右顶点分别为A1,A2,点
的左、右顶点分别为A1,A2,点 ,
,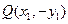 是双曲线上不同的两个动点。
是双曲线上不同的两个动点。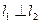 ,求h的值。
,求h的值。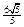 km区域;在直线x=2的左侧,考察范围为到A,B两点的距离之和不超过
km区域;在直线x=2的左侧,考察范围为到A,B两点的距离之和不超过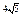 km区域。
km区域。

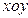 中,如图,已知椭圆
中,如图,已知椭圆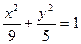 的左右顶点为A,B,右顶点为F,设过点T(
的左右顶点为A,B,右顶点为F,设过点T(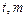 )的直线TA,TB与椭圆分别交于点M
)的直线TA,TB与椭圆分别交于点M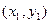 ,
,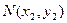 ,其中m>0,
,其中m>0,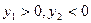

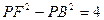 ,求点P的轨迹
,求点P的轨迹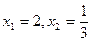 ,求点T的坐标
,求点T的坐标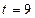 ,求证:直线MN必过x轴上的一定点
,求证:直线MN必过x轴上的一定点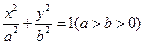 的左焦点为F,过点F的直线与椭圆C相交于A,B两点,直线l的倾斜角为60o,
的左焦点为F,过点F的直线与椭圆C相交于A,B两点,直线l的倾斜角为60o,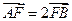 .
.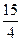 ,求椭圆C的方程.
,求椭圆C的方程.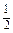 ,不在x轴上的动点P与点F的距离是它到直线l的距离的2倍.设点P的轨迹为E,过点F的直线交E于B、C两点,直线AB、AC分别交l于点M、N
,不在x轴上的动点P与点F的距离是它到直线l的距离的2倍.设点P的轨迹为E,过点F的直线交E于B、C两点,直线AB、AC分别交l于点M、N

 w_w w. k#s5_u.c o*m
w_w w. k#s5_u.c o*m 的离心率
的离心率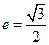 ,连接椭圆的四个顶点得到的菱形的面积为4。
,连接椭圆的四个顶点得到的菱形的面积为4。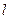 与椭圆相交于不同的两点
与椭圆相交于不同的两点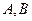 ,已知点
,已知点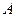 的坐标为(
的坐标为(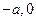 ),点
),点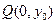 在线段
在线段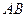 的垂直平分线上,且
的垂直平分线上,且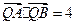 ,求
,求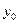 的值
的值 .
. 若存在,求出点P的坐标;若不存在,说明理由。
若存在,求出点P的坐标;若不存在,说明理由。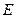 经过点
经过点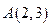 ,对称轴为
,对称轴为 坐标轴,焦点
坐标轴,焦点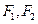 在
在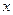 轴上,离心率
轴上,离心率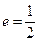 。[来源:学科网ZXXK]
。[来源:学科网ZXXK]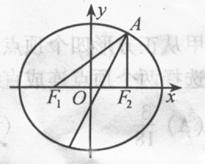
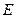 的方程;
的方程;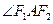 的角平分线所在直线
的角平分线所在直线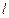 的方程;
的方程;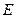 上是否存在关于直线
上是否存在关于直线
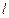 对称的相异两点?若存在,请找出;若不存在,说明理由。
对称的相异两点?若存在,请找出;若不存在,说明理由。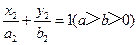 的离心率为
的离心率为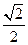 ,以该椭圆上的点和椭圆的左、右焦点
,以该椭圆上的点和椭圆的左、右焦点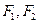 为顶点的三角形的周长为
为顶点的三角形的周长为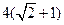 .一等轴双曲线的顶点是该椭圆的焦点,设
.一等轴双曲线的顶点是该椭圆的焦点,设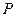 为该双曲线上异于顶点的任一点,直线
为该双曲线上异于顶点的任一点,直线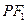 和
和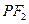 与椭圆的交点分别为
与椭圆的交点分别为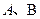 和
和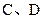 .
.
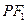 、
、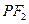 的斜率分别为
的斜率分别为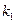 、
、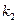 ,证明
,证明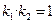 ;
;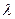 ,使得
,使得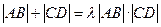 恒成立?若存在,求
恒成立?若存在,求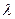 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
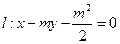 ,
,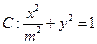 ,
,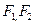 分别为椭圆
分别为椭圆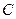 的左、右焦点.
的左、右焦点. 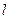 过右焦点
过右焦点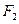 时,求直线
时,求直线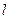 的方程;
的方程;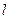 与椭圆
与椭圆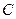 交于
交于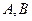 两点,
两点,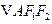 ,
,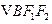 的重心分别为
的重心分别为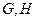 .若原点
.若原点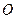 在以线段
在以线段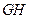 为直径的圆内,求实数
为直径的圆内,求实数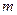 的取值范围.
的取值范围.