适用年级:{{getGradeNameByProperty('高三|专题试卷|全国|2014年')}} 试卷类型:{{getTestPaperTypeName('高三|专题试卷|全国|2014年')}} 使用省份:{{getAreaName('高三|专题试卷|全国|2014年')}}
试卷年份:{{getYear('高三|专题试卷|全国|2014年')}}上传日期:2014-03-13题数:11
提示:单击题文可显示答案与解析。
题号:949393
题型:选择题
难易度:一般
日期:2014-03-13
来源:2014年高考数学(理)二轮复习专题提升训练6练习卷(带解析)
【题文】已知函数
f(
x)=sin (2
x+
φ),其中
φ为实数,若
f(
x)≤
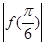
对
x∈R恒成立,且
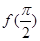
<
f(π),则下列结论正确的是( ).
A.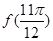 =-1 =-1 |
B.f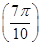 >f >f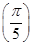 |
| C.f(x)是奇函数 |
D.f(x)的单调递增区间是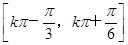 (k∈Z) (k∈Z) |
题号:949394
题型:选择题
难易度:较易
日期:2014-03-13
来源:2014年高考数学(理)二轮复习专题提升训练6练习卷(带解析)
【题文】已知函数
f(
x)=2sin(
ωx+
φ)(
ω>0)的图象关于直线
x=
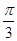
对称,且
f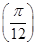
=0,则
ω的最小值为( ).
题号:949395
题型:选择题
难易度:较易
日期:2014-03-13
来源:2014年高考数学(理)二轮复习专题提升训练6练习卷(带解析)
【题文】将函数
y=sin
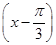
的图象上所有点的横坐标伸长到原来的2倍(纵坐标不变),再将所得图象向左平移
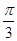
个单位,则所得函数图象对应的解析式为( ).
A.y=sin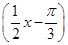 | B.y=sin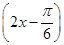 |
C.y=sin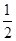 x x | D.y=sin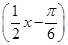 |
题号:4187939
题型:选择题
难易度:较易
日期:2014-03-14
来源:2014年高考数学(理)二轮复习专题提升训练6练习卷(带解析)
【题文】已知函数
f(
x)=
Acos(
ωx+
φ)(
A>0,
ω>0,
φ∈R),则“
f(
x)是奇函数”是“
φ=
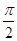
”的( ).
| A.充分不必要条件 | B.必要不充分条件 |
| C.充分必要条件 | D.既不充分也不必要条件 |
题号:4187940
题型:选择题
难易度:较易
日期:2014-03-14
来源:2014年高考数学(理)二轮复习专题提升训练6练习卷(带解析)
【题文】将函数
y=
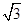
cos
x+sin
x(
x∈R) 的图象向左平移
m(
m>0)个单位长度后,所得到的图象关于
y轴对称,则
m的最小值是( ).
题号:3598849
题型:填空题
难易度:一般
日期:2014-03-14
来源:2014年高考数学(理)二轮复习专题提升训练6练习卷(带解析)
【题文】已知函数
f(
x)=3sin(
ωx-
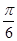
)(
ω>0)和
g(
x)=3cos(2
x+
φ)的图象的对称中心完全相同,若
x∈
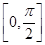
,则
f(
x)的取值范围是______.
题号:4187941
题型:填空题
难易度:容易
日期:2014-03-14
来源:2014年高考数学(理)二轮复习专题提升训练6练习卷(带解析)
题号:4187942
题型:填空题
难易度:一般
日期:2014-03-14
来源:2014年高考数学(理)二轮复习专题提升训练6练习卷(带解析)
【题文】若函数
f(
x)=sin
ωx(
ω>0)在区间
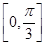
上单调递增,在区间
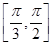
上单调递减,则
ω=________.
题号:949371
题型:解答题
难易度:较易
日期:2014-03-13
来源:2014年高考数学(理)二轮复习专题提升训练6练习卷(带解析)
【题文】已知函数
f(
x)=2sin
ωx·cos
ωx+2
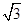
cos
2ωx-
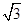
(其中
ω>0),且函数
f(
x)的周期为π.
(1)求
ω的值;
(2)将函数
y=
f(
x)的图象向右平移
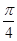
个单位长度,再将所得图象各点的横坐标缩小到原来的
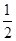
倍(纵坐标不变)得到函数
y=
g(
x)的图象,求函数
g(
x)在
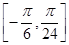
上的单调区间.
题号:949392
题型:解答题
难易度:较易
日期:2014-03-13
来源:2014年高考数学(理)二轮复习专题提升训练6练习卷(带解析)
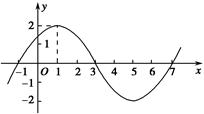
【题文】已知函数
f(
x)=
Asin(
ωx+
φ)(
A>0,
ω>0,|
φ|<
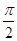
)的图象的一部分如图所示.
(1)求函数
f(
x)的解析式;
(2)当
x∈
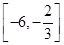
时,求函数
y=
f(
x)+
f(
x+2)的最大值与最小值及相应的
x的值.
题号:4187943
题型:解答题
难易度:较易
日期:2014-03-14
来源:2014年高考数学(理)二轮复习专题提升训练6练习卷(带解析)
【题文】已知函数
f(
x)=sin
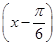
+cos
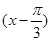
,
g(
x)=2sin
2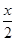
.
(1)若
α是第一象限角,且
f(
α)=
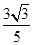
.求
g(
α)的值;
(2)求使
f(
x)≥
g(
x)成立的
x的取值集合.
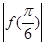 对x∈R恒成立,且
对x∈R恒成立,且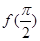 <f(π),则下列结论正确的是( ).
<f(π),则下列结论正确的是( ).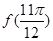 =-1
=-1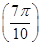 >f
>f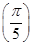
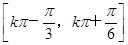 (k∈Z)
(k∈Z)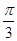 对称,且f
对称,且f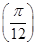 =0,则ω的最小值为( ).
=0,则ω的最小值为( ).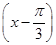 的图象上所有点的横坐标伸长到原来的2倍(纵坐标不变),再将所得图象向左平移
的图象上所有点的横坐标伸长到原来的2倍(纵坐标不变),再将所得图象向左平移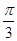 个单位,则所得函数图象对应的解析式为( ).
个单位,则所得函数图象对应的解析式为( ).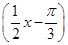
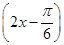
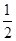 x
x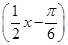
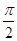 ”的( ).
”的( ).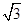 cos x+sin x(x∈R) 的图象向左平移m(m>0)个单位长度后,所得到的图象关于y轴对称,则m的最小值是( ).
cos x+sin x(x∈R) 的图象向左平移m(m>0)个单位长度后,所得到的图象关于y轴对称,则m的最小值是( ).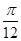
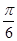
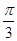
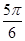
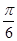 )(ω>0)和g(x)=3cos(2x+φ)的图象的对称中心完全相同,若x∈
)(ω>0)和g(x)=3cos(2x+φ)的图象的对称中心完全相同,若x∈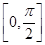 ,则f(x)的取值范围是______.
,则f(x)的取值范围是______.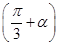 =
=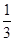 ,则sin
,则sin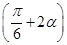 =______.
=______.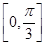 上单调递增,在区间
上单调递增,在区间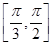 上单调递减,则ω=________.
上单调递减,则ω=________.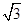 cos2ωx-
cos2ωx-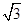 (其中ω>0),且函数f(x)的周期为π.
(其中ω>0),且函数f(x)的周期为π.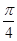 个单位长度,再将所得图象各点的横坐标缩小到原来的
个单位长度,再将所得图象各点的横坐标缩小到原来的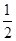 倍(纵坐标不变)得到函数y=g(x)的图象,求函数g(x)在
倍(纵坐标不变)得到函数y=g(x)的图象,求函数g(x)在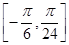 上的单调区间.
上的单调区间.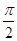 )的图象的一部分如图所示.
)的图象的一部分如图所示.
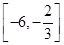 时,求函数y=f(x)+f(x+2)的最大值与最小值及相应的x的值.
时,求函数y=f(x)+f(x+2)的最大值与最小值及相应的x的值.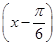 +cos
+cos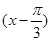 ,g(x)=2sin2
,g(x)=2sin2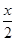 .
.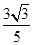 .求g(α)的值;
.求g(α)的值;