适用年级:{{getGradeNameByProperty('高三|专题试卷|全国|2014年')}} 试卷类型:{{getTestPaperTypeName('高三|专题试卷|全国|2014年')}} 使用省份:{{getAreaName('高三|专题试卷|全国|2014年')}}
试卷年份:{{getYear('高三|专题试卷|全国|2014年')}}上传日期:2014-03-17题数:11
提示:单击题文可显示答案与解析。
题号:948401
题型:选择题
难易度:较难
日期:2014-03-17
来源:2014年高考数学(理)二轮专题复习知能提升演练1-6-2练习卷(带解析)
【题文】设椭圆
C:
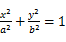
(
a>
b>0)的左、右焦点分别为
F1,
F2,
P是
C上的点,
PF2⊥
F1F2,∠
PF1F2=30°,则
C的离心率为 ( )
题号:948402
题型:选择题
难易度:较易
日期:2014-03-17
来源:2014年高考数学(理)二轮专题复习知能提升演练1-6-2练习卷(带解析)
【题文】抛物线
y2=4
x的焦点到双曲线
x2-
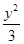
=1的渐近线的距离是( ).
题号:4187725
题型:选择题
难易度:较易
日期:2014-03-18
来源:2014年高考数学(理)二轮专题复习知能提升演练1-6-2练习卷(带解析)
【题文】已知中心在原点的双曲线
C的右焦点为
F(3,0),离心率等于
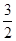
,则
C的方程是( ).
题号:4187726
题型:选择题
难易度:较难
日期:2014-03-18
来源:2014年高考数学(理)二轮专题复习知能提升演练1-6-2练习卷(带解析)
【题文】
O为坐标原点,
F为抛物线
C:
y2=4
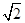 x
x的焦点,
P为
C上一点,若|
PF|=4
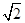
,则△
POF的面积为( ).
| A.2 | B.2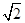 | C.2 | D.4 |
题号:4187727
题型:选择题
难易度:一般
日期:2014-03-18
来源:2014年高考数学(理)二轮专题复习知能提升演练1-6-2练习卷(带解析)
【题文】抛物线
C1:
y=
 x2
x2(
p>0)的焦点与双曲线
C2:
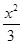
-
y2=1的右焦点的连线交
C1于第一象限的点
M.若
C1在点
M处的切线平行于
C2的一条渐近线,则
p=( ).
题号:948400
题型:填空题
难易度:一般
日期:2014-03-17
来源:2014年高考数学(理)二轮专题复习知能提升演练1-6-2练习卷(带解析)
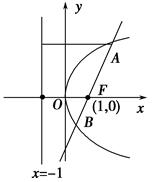
【题文】过抛物线
y2=4
x的焦点
F的直线交该抛物线于
A,
B两点.若|
AF|=3,
则|
BF|=________.
题号:4187728
题型:填空题
难易度:较易
日期:2014-03-18
来源:2014年高考数学(理)二轮专题复习知能提升演练1-6-2练习卷(带解析)
【题文】已知抛物线
y2=8
x的准线过双曲线
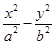
=1(
a>0,
b>0)的一个焦点,且双曲线的离心率为2,则该双曲线的方程为________.
题号:4187729
题型:填空题
难易度:一般
日期:2014-03-18
来源:2014年高考数学(理)二轮专题复习知能提升演练1-6-2练习卷(带解析)
【题文】椭圆
T:
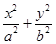
=1(
a>
b>0)的左,右焦点分别为
F1,
F2,焦距为2
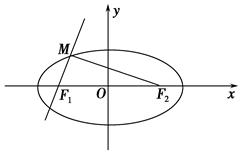
c.若直线
y=

(
x+
c)与椭圆
T的一个交点
M满足∠
MF1F2=2∠
MF2F1,则该椭圆的离心率等于________.
题号:948398
题型:解答题
难易度:较难
日期:2014-03-17
来源:2014年高考数学(理)二轮专题复习知能提升演练1-6-2练习卷(带解析)
【题文】已知椭圆
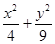
=1上任一点
P,由点
P向
x轴作垂线
PQ,垂足为
Q,设点
M在
PQ上,且
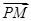
=2
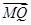
,点
M的轨迹为
C.
(1)求曲线
C的方程;
(2)过点
D(0,-2)作直线
l与曲线
C交于
A、
B两点,设
N是过点
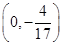
且平行于
x轴的直线上一动点,且满足
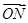
=
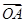
+
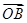
(
O为原点),且四边形
OANB为矩形,求直线
l的方程.
题号:948399
题型:解答题
难易度:较难
日期:2014-03-17
来源:2014年高考数学(理)二轮专题复习知能提升演练1-6-2练习卷(带解析)
【题文】已知椭圆
C1:
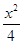
+
y2=1,椭圆
C2以
C1的长轴为短轴,且与
C1有相同的离心率.
(1)求椭圆
C2的方程;
(2)设
O为坐标原点,点
A,
B分别在椭圆
C1和
C2上,
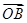
=2
,求直线
AB的方程.
题号:4187730
题型:解答题
难易度:较难
日期:2014-03-18
来源:2014年高考数学(理)二轮专题复习知能提升演练1-6-2练习卷(带解析)
【题文】如图,抛物线
E:
y2=4
x的焦点为
F,准线
l与
x轴的交点为
A.点
C在抛物线
E上,以
C为圆心,|
CO|为半径作圆,设圆
C与准线
l交于不同的两点
M,
N.
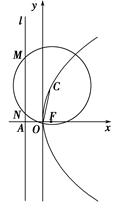
(1)若点
C的纵坐标为2,求|
MN|;
(2)若|
AF|
2=|
AM|·|
AN|,求圆
C的半径.
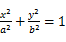 (a>b>0)的左、右焦点分别为F1,F2, P是C上的点,PF2⊥F1F2,∠PF1F2=30°,则C的离心率为 ( )
(a>b>0)的左、右焦点分别为F1,F2, P是C上的点,PF2⊥F1F2,∠PF1F2=30°,则C的离心率为 ( )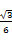


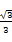
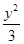 =1的渐近线的距离是( ).
=1的渐近线的距离是( ).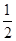
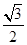

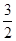 ,则C的方程是( ).
,则C的方程是( ). =1
=1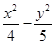 =1
=1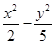 =1
=1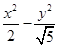 =1
=1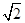 x的焦点,P为C上一点,若|PF|=4
x的焦点,P为C上一点,若|PF|=4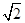 ,则△POF的面积为( ).
,则△POF的面积为( ).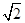

 x2(p>0)的焦点与双曲线C2:
x2(p>0)的焦点与双曲线C2: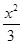 -y2=1的右焦点的连线交C1于第一象限的点M.若C1在点M处的切线平行于C2的一条渐近线,则p=( ).
-y2=1的右焦点的连线交C1于第一象限的点M.若C1在点M处的切线平行于C2的一条渐近线,则p=( ).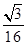
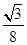
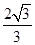
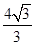

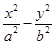 =1(a>0,b>0)的一个焦点,且双曲线的离心率为2,则该双曲线的方程为________.
=1(a>0,b>0)的一个焦点,且双曲线的离心率为2,则该双曲线的方程为________.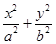 =1(a>b>0)的左,右焦点分别为F1,F2,焦距为2c.若直线y=
=1(a>b>0)的左,右焦点分别为F1,F2,焦距为2c.若直线y= (x+c)与椭圆T的一个交点M满足∠MF1F2=2∠MF2F1,则该椭圆的离心率等于________.
(x+c)与椭圆T的一个交点M满足∠MF1F2=2∠MF2F1,则该椭圆的离心率等于________.
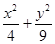 =1上任一点P,由点P向x轴作垂线PQ,垂足为Q,设点M在PQ上,且
=1上任一点P,由点P向x轴作垂线PQ,垂足为Q,设点M在PQ上,且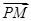 =2
=2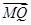 ,点M的轨迹为C.
,点M的轨迹为C.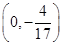 且平行于x轴的直线上一动点,且满足
且平行于x轴的直线上一动点,且满足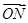 =
=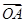 +
+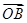 (O为原点),且四边形OANB为矩形,求直线l的方程.
(O为原点),且四边形OANB为矩形,求直线l的方程.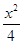 +y2=1,椭圆C2以C1的长轴为短轴,且与C1有相同的离心率.
+y2=1,椭圆C2以C1的长轴为短轴,且与C1有相同的离心率.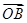 =2
=2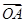 ,求直线AB的方程.
,求直线AB的方程.