适用年级:{{getGradeNameByProperty('高三|专题试卷|全国|2010年')}} 试卷类型:{{getTestPaperTypeName('高三|专题试卷|全国|2010年')}} 使用省份:{{getAreaName('高三|专题试卷|全国|2010年')}}
试卷年份:{{getYear('高三|专题试卷|全国|2010年')}}上传日期:2010-06-28题数:20
提示:单击题文可显示答案与解析。
题号:1260261
题型:选择题
难易度:一般
日期:2010-06-18
来源:2010年高考试题分项版文科数学之专题十三 导数
题号:1260619
题型:选择题
难易度:一般
日期:2010-06-18
来源:2010年高考试题分项版文科数学之专题十三 导数
【题文】

题号:1261837
题型:选择题
难易度:一般
日期:2010-06-15
来源:2010年高考试题分项版文科数学之专题十三 导数
【题文】已知点
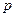
在曲线
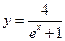
上,
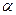
为曲线在点
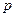
处的切线的倾斜角,则
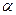
的取值范围是
(A)[0,
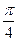
) (B)
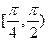
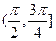
(D)
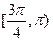
题号:1261957
题型:选择题
难易度:一般
日期:2010-06-15
来源:2010年高考试题分项版文科数学之专题十三 导数
题号:1262239
题型:选择题
难易度:一般
日期:2010-06-15
来源:2010年高考试题分项版文科数学之专题十三 导数
【题文】曲线
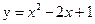
在点(1,0)处的切线方程为
题号:4216986
题型:选择题
难易度:较难
日期:2012-06-13
来源:2010年高考试题分项版文科数学之专题十三 导数
【题文】观察
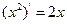
,
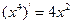
,
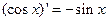
,由归纳推理可得:若定义在
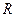
上的函数
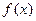
满足
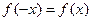
,记
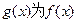
的导函数,则
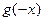
题号:1087326
题型:解答题
难易度:一般
日期:2012-04-20
来源:2010年高考试题分项版文科数学之专题十三 导数
【题文】设函数

.
(1)若

的两个极值点为

,且
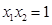
,求实数
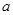
的值;
(2)是否存在实数
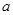
,使得

是
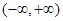
上的单调函数?若存在,求出
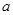
的值;若不存在,说明理由.
题号:1258625
题型:解答题
难易度:较难
日期:2010-06-23
来源:2010年高考试题分项版文科数学之专题十三 导数
【题文】(本小题满分12分)(注意:在试题卷上作答无效)
已知函数

.
(Ⅰ)当

时,求

的极值;
(Ⅱ)若

在
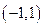
上是增函数,求
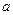
的取值范围.
题号:1261293
题型:解答题
难易度:一般
日期:2010-06-17
来源:2010年高考试题分项版文科数学之专题十三 导数
【题文】已知函数
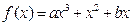
(其中常数a,b∈R),

是奇函数.
(Ⅰ)求
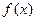
的表达式;
(Ⅱ)讨论

的单调性,并求

在区间[1,2]上的最大值和最小值.
题号:1261629
题型:解答题
难易度:一般
日期:2010-06-17
来源:2010年高考试题分项版文科数学之专题十三 导数
【题文】已知函数

其中a<0,且a≠-1.
(Ⅰ)讨论函数
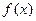
的单调性;
(Ⅱ)设函数
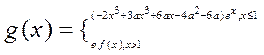
(e是自然数的底数)。是否存在a,使
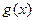
在[a,-a]上为减函数?若存在,求a的取值范围;若不存在,请说明理由。
题号:1261946
题型:解答题
难易度:一般
日期:2010-06-15
来源:2010年高考试题分项版文科数学之专题十三 导数
【题文】 已知函数f(x)=x
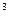
-3ax
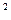
+3x+1。
(Ⅰ)设a=2,求f(x)的单调期间;
(Ⅱ)设f(x)在区间(2,3)中至少有一个极值点,求a的取值范围。
题号:1262093
题型:解答题
难易度:一般
日期:2010-06-15
来源:2010年高考试题分项版文科数学之专题十三 导数
【题文】设函数
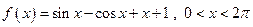
,求函数
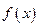
的单调区间与极值。
题号:1262225
题型:解答题
难易度:一般
日期:2010-06-15
来源:2010年高考试题分项版文科数学之专题十三 导数
【题文】设函数
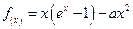
(Ⅰ)若a=
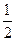
,求
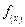
的单调区间;
(Ⅱ)若当
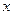
≥0时
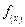
≥0,求a的取值范围
题号:1262914
题型:解答题
难易度:较难
日期:2010-06-11
来源:2010年高考试题分项版文科数学之专题十三 导数
【题文】
已知函数

(a-b)
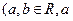
<b)。
(I)当a=1,b=2时,求曲线

在点(2,

)处的切线方程。
(II)设
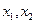
是

的两个极值点,
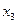
是

的一个零点,且
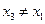
,

证明:存在实数
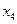
,使得

按某种顺序排列后的等差数列,并求
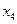
题号:1263279
题型:解答题
难易度:一般
日期:2010-06-11
来源:2010年高考试题分项版文科数学之专题十三 导数
【题文】(本小题满分14分)
已知函数
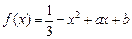
的图像在点P(0,f(0))处的切线方程为

.
(Ⅰ)求实数a,b的值;
(Ⅱ)设

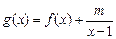
是
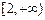
上的增函数.
(ⅰ)求实数m的最大值;
(ⅱ)当m取最大值时,是否存在点Q,使得过点Q的直线能与曲线
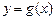
围成两个封闭图形,则这两个封闭图形的面积总相等?若存在,求出点Q的坐标;若不存在,说明理由.
题号:3757453
题型:解答题
难易度:较易
日期:2013-05-24
来源:2010年高考试题分项版文科数学之专题十三 导数
【题文】(本小题共14分)
设定函数

,且方程

的两个根分别为1,4。
(Ⅰ)当a=3且曲线

过原点时,求
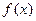
的解析式;
(Ⅱ)若
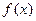
在
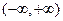
无极值点,求a的取值范围。
题号:3766990
题型:解答题
难易度:一般
日期:2012-06-08
来源:2010年高考试题分项版文科数学之专题十三 导数
【题文】已知函数
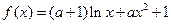
.
(Ⅰ)讨论函数
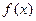
的单调性;
K^S*5U.C#(Ⅱ)设
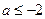
,证明:对任意
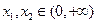
,
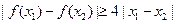
。
题号:3767476
题型:解答题
难易度:一般
日期:2013-07-25
来源:2010年高考试题分项版文科数学之专题十三 导数
【题文】设函数
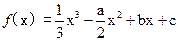
,其中a>0,曲线
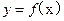
在点P(0,
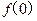
)处的切线方程为y=1
(Ⅰ)确定b、c的值
(Ⅱ)设曲线
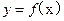
在点(
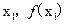
)及(
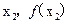
)处的切线都过点(0,2)证明:当
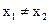
时,
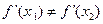
(Ⅲ)若过点(0,2)可作曲线
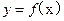
的三条不同切线,求a的取值范围。
题号:3767733
题型:解答题
难易度:一般
日期:2012-07-10
来源:2010年高考试题分项版文科数学之专题十三 导数
【题文】(本小题满分12分)
已知函数f(x)=
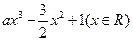
,其中a>0.
(Ⅰ)若a=1,求曲线y=f(x)在点(2,f(2))处的切线方程;
(Ⅱ)若在区间

上,f(x)>0恒成立,求a的取值范围.
题号:3877090
题型:解答题
难易度:较难
日期:2013-05-24
来源:2010年高考试题分项版文科数学之专题十三 导数
【题文】(本小题满分14分)
已知函数

,
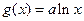
,
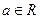
.
(Ⅰ)若曲线
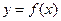
与曲线
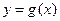
相交,且在交点处有相同的切线,求
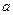
的值及该切线的方程;
(Ⅱ)设函数
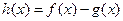
,当
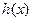
存在最小值时,求其最小值

的解析式;
(Ⅲ)对(Ⅱ)中的

,证明:当
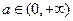
时,
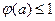
.
 满足
满足 ,则
,则
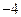
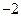

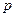 在曲线
在曲线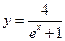 上,
上,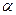 为曲线在点
为曲线在点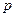 处的切线的倾斜角,则
处的切线的倾斜角,则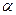 的取值范围是
的取值范围是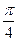 ) (B)
) (B)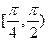
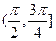 (D)
(D) 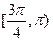
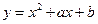 在点
在点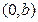 处的切线方程是
处的切线方程是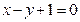 ,则
,则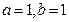
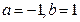
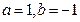
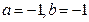
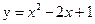 在点(1,0)处的切线方程为
在点(1,0)处的切线方程为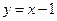
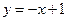
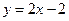
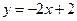
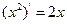 ,
,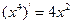 ,
,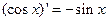 ,由归纳推理可得:若定义在
,由归纳推理可得:若定义在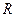 上的函数
上的函数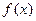 满足
满足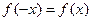 ,记
,记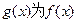 的导函数,则
的导函数,则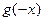
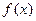
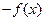
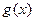
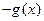
 .
. 的两个极值点为
的两个极值点为 ,且
,且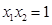 ,求实数
,求实数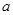 的值;
的值;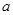 ,使得
,使得 是
是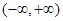 上的单调函数?若存在,求出
上的单调函数?若存在,求出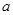 的值;若不存在,说明理由.
的值;若不存在,说明理由. .
. 时,求
时,求 的极值;
的极值; 在
在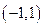 上是增函数,求
上是增函数,求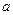 的取值范围.
的取值范围.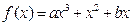 (其中常数a,b∈R),
(其中常数a,b∈R), 是奇函数.
是奇函数.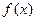 的表达式;
的表达式; 的单调性,并求
的单调性,并求 在区间[1,2]上的最大值和最小值.
在区间[1,2]上的最大值和最小值. 其中a<0,且a≠-1.
其中a<0,且a≠-1.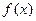 的单调性;
的单调性;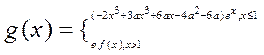 (e是自然数的底数)。是否存在a,使
(e是自然数的底数)。是否存在a,使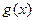 在[a,-a]上为减函数?若存在,求a的取值范围;若不存在,请说明理由。
在[a,-a]上为减函数?若存在,求a的取值范围;若不存在,请说明理由。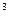 -3ax
-3ax +3x+1。
+3x+1。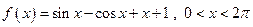 ,求函数
,求函数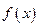 的单调区间与极值。
的单调区间与极值。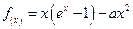
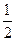 ,求
,求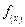 的单调区间;
的单调区间;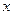 ≥0时
≥0时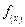 ≥0,求a的取值范围
≥0,求a的取值范围 (a-b)
(a-b)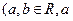 <b)。
<b)。 在点(2,
在点(2, )处的切线方程。
)处的切线方程。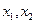 是
是 的两个极值点,
的两个极值点,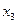 是
是 的一个零点,且
的一个零点,且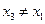 ,
,
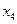 ,使得
,使得 按某种顺序排列后的等差数列,并求
按某种顺序排列后的等差数列,并求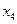
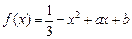 的图像在点P(0,f(0))处的切线方程为
的图像在点P(0,f(0))处的切线方程为 .
.
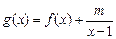 是
是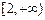 上的增函数.
上的增函数.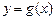 围成两个封闭图形,则这两个封闭图形的面积总相等?若存在,求出点Q的坐标;若不存在,说明理由.
围成两个封闭图形,则这两个封闭图形的面积总相等?若存在,求出点Q的坐标;若不存在,说明理由. ,且方程
,且方程 的两个根分别为1,4。
的两个根分别为1,4。 过原点时,求
过原点时,求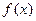 的解析式;
的解析式;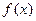 在
在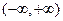 无极值点,求a的取值范围。
无极值点,求a的取值范围。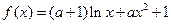 .
.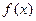 的单调性; K^S*5U.C#
的单调性; K^S*5U.C#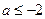 ,证明:对任意
,证明:对任意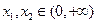 ,
,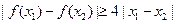 。
。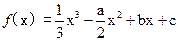 ,其中a>0,曲线
,其中a>0,曲线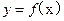 在点P(0,
在点P(0,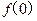 )处的切线方程为y=1
)处的切线方程为y=1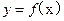 在点(
在点(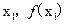 )及(
)及(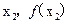 )处的切线都过点(0,2)证明:当
)处的切线都过点(0,2)证明:当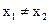 时,
时,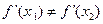
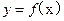 的三条不同切线,求a的取值范围。
的三条不同切线,求a的取值范围。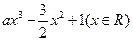 ,其中a>0.
,其中a>0.  上,f(x)>0恒成立,求a的取值范围.
上,f(x)>0恒成立,求a的取值范围. ,
,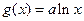 ,
,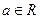 .
. 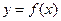 与曲线
与曲线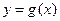 相交,且在交点处有相同的切线,求
相交,且在交点处有相同的切线,求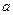 的值及该切线的方程;
的值及该切线的方程;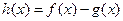 ,当
,当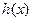 存在最小值时,求其最小值
存在最小值时,求其最小值 的解析式;
的解析式; ,证明:当
,证明:当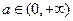 时,
时,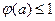 .
.