适用年级:{{getGradeNameByProperty('高三|专题试卷|全国|2010年')}} 试卷类型:{{getTestPaperTypeName('高三|专题试卷|全国|2010年')}} 使用省份:{{getAreaName('高三|专题试卷|全国|2010年')}}
试卷年份:{{getYear('高三|专题试卷|全国|2010年')}}上传日期:2010-06-28题数:9
提示:单击题文可显示答案与解析。
题号:4216986
题型:选择题
难易度:较难
日期:2012-06-13
来源:2010年高考试题分项版文科数学之专题十五 推理与证明
【题文】观察
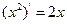
,
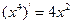
,
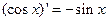
,由归纳推理可得:若定义在
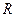
上的函数
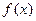
满足
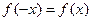
,记
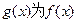
的导函数,则
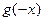
题号:1258610
题型:填空题
难易度:较难
日期:2010-06-23
来源:2010年高考试题分项版文科数学之专题十五 推理与证明
【题文】观察下列等式:

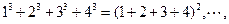
根据上述规律,第四个等式为
.
题号:1263287
题型:填空题
难易度:一般
日期:2010-06-11
来源:2010年高考试题分项版文科数学之专题十五 推理与证明
【题文】观察下列等式:
① cos2α="2" cos
2 α-1;
② cos 4α="8" cos
4 α-8 cos
2 α+1;
③ cos 6α="32" cos
6 α-48 cos
4 α+18 cos
2 α-1;
④ cos 8α=" 128" co

s
8α-256cos
6 α+160 cos
4 α-32 cos
2 α+1;
⑤ cos 10α=mcos
10α-1280 cos
8α+1120cos
6 α+ncos
4 α+p cos
2 α-1;
可以推测,m-n+p=
.
题号:1263289
题型:填空题
难易度:一般
日期:2010-06-11
来源:2010年高考试题分项版文科数学之专题十五 推理与证明
【题文】对于平面上的点集Ω,如果连接Ω中任意两点的线段必定包涵Ω,则称Ω为平面上的凸集,给出平面上4个点集的图形如下(阴影区域及其边界):
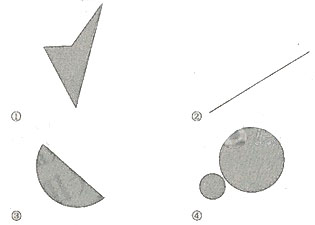
其中为凸集的是
(写出所有凸集相应图形的序号).
题号:1258166
题型:解答题
难易度:较难
日期:2010-06-23
来源:2010年高考试题分项版文科数学之专题十五 推理与证明
【题文】(本小题满分14分)
已知曲线

,点
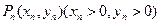
是曲线

上的点
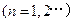
.
(1)试写出曲线

在点

处的切线
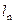
的方程,并求出
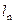
与
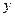
轴的交点

的坐标;
(2)若原点
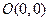
到
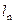
的距离与线段
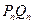
的长度之比取得最大值,试求试点

的坐标
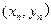
;
(3)设

与
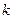
为两个给定的不同的正整数,
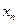
与

是满足(2)中条件的点

的坐标,
证明:


题号:1260247
题型:解答题
难易度:一般
日期:2010-06-18
来源:2010年高考试题分项版文科数学之专题十五 推理与证明
【题文】正实数数列
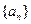
中,
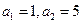
,且
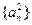
成等差数列.
(1) 证明数列
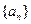
中有无穷多项为无理数;
(2)当
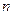
为何值时,
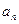
为整数,并求出使
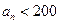
的所有整数项的和.
题号:1261630
题型:解答题
难易度:一般
日期:2010-06-17
来源:2010年高考试题分项版文科数学之专题十五 推理与证明
【题文】给出下面的数表序列:

其中表n(n="1,2,3"

)有n行,第1行的n个数是1,3,5,

2n-1,从第2行起,每行中的每个数都等于它肩上的两数之和。
(I)写出表4,验证表4各行中数的平均数按从上到下的顺序构成等比数列,并将结论推广到表n(n≥3)(不要求证明);
(II)每个数列中最后一行都只有一个数,它们构成数列1,4,12

,记此数列为
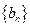
求和:
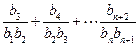

题号:1263930
题型:解答题
难易度:较易
日期:2010-06-09
来源:2010年高考试题分项版文科数学之专题十五 推理与证明
【题文】(本小题共13分)
已知集合
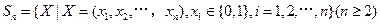
对于
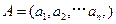
,
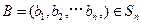
,定义A与B的差为

A与B之间的距离为

(Ⅰ)当n=5时,设
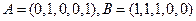
,求
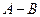
,

;
(Ⅱ)证明:

,且

;
(Ⅲ) 证明:
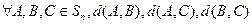
三个数中至少有一个是偶数
题号:3767476
题型:解答题
难易度:一般
日期:2013-07-25
来源:2010年高考试题分项版文科数学之专题十五 推理与证明
【题文】设函数
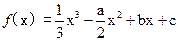
,其中a>0,曲线
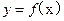
在点P(0,
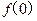
)处的切线方程为y=1
(Ⅰ)确定b、c的值
(Ⅱ)设曲线
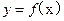
在点(
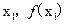
)及(
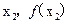
)处的切线都过点(0,2)证明:当
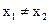
时,
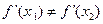
(Ⅲ)若过点(0,2)可作曲线
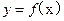
的三条不同切线,求a的取值范围。
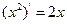 ,
,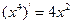 ,
,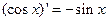 ,由归纳推理可得:若定义在
,由归纳推理可得:若定义在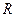 上的函数
上的函数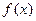 满足
满足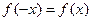 ,记
,记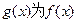 的导函数,则
的导函数,则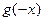
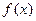
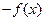
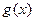

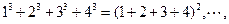 根据上述规律,第四个等式为 .
根据上述规律,第四个等式为 . s8α-256cos6 α+160 cos4 α-32 cos2 α+1;
s8α-256cos6 α+160 cos4 α-32 cos2 α+1;
 ,点
,点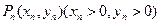 是曲线
是曲线 上的点
上的点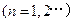 .
. 在点
在点 处的切线
处的切线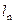 的方程,并求出
的方程,并求出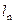 与
与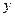 轴的交点
轴的交点 的坐标;
的坐标;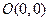 到
到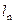 的距离与线段
的距离与线段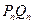 的长度之比取得最大值,试求试点
的长度之比取得最大值,试求试点 的坐标
的坐标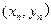 ;
; 与
与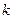 为两个给定的不同的正整数,
为两个给定的不同的正整数,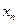 与
与 是满足(2)中条件的点
是满足(2)中条件的点 的坐标,
的坐标,

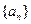 中,
中,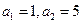 ,且
,且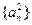 成等差数列.
成等差数列.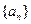 中有无穷多项为无理数;
中有无穷多项为无理数;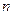 为何值时,
为何值时,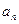 为整数,并求出使
为整数,并求出使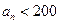 的所有整数项的和.
的所有整数项的和.
 )有n行,第1行的n个数是1,3,5,
)有n行,第1行的n个数是1,3,5, 2n-1,从第2行起,每行中的每个数都等于它肩上的两数之和。
2n-1,从第2行起,每行中的每个数都等于它肩上的两数之和。 ,记此数列为
,记此数列为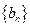 求和:
求和: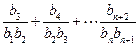

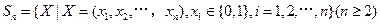 对于
对于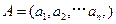 ,
,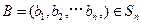 ,定义A与B的差为
,定义A与B的差为

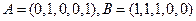 ,求
,求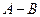 ,
, ;
; ,且
,且 ;
;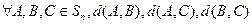 三个数中至少有一个是偶数
三个数中至少有一个是偶数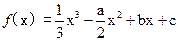 ,其中a>0,曲线
,其中a>0,曲线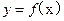 在点P(0,
在点P(0,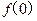 )处的切线方程为y=1
)处的切线方程为y=1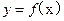 在点(
在点(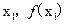 )及(
)及(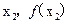 )处的切线都过点(0,2)证明:当
)处的切线都过点(0,2)证明:当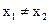 时,
时,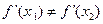
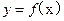 的三条不同切线,求a的取值范围。
的三条不同切线,求a的取值范围。