适用年级:{{getGradeNameByProperty('高一|专题试卷|全国|2019年')}} 试卷类型:{{getTestPaperTypeName('高一|专题试卷|全国|2019年')}} 使用省份:{{getAreaName('高一|专题试卷|全国|2019年')}}
试卷年份:{{getYear('高一|专题试卷|全国|2019年')}}上传日期:2018-10-28题数:16
提示:单击题文可显示答案与解析。
题号:748135
题型:选择题
难易度:一般
日期:2016-05-18
来源:《2018-2019学年同步单元双基双测AB卷》必修一 专题八 函数模型与应用 A卷
【题文】国家规定个人稿费纳税办法为:不超过800元的不纳税;超过800元而不超过4000元的按超过部分的14%纳税;超过4000元的按全稿酬的11%纳税.某人出版了一本书共纳税420元,则他的稿费为( )
| A.3000元 | B.3800元 | C.3818元 | D.5600元 |
题号:763377
题型:选择题
难易度:较易
日期:2016-03-28
来源:《2018-2019学年同步单元双基双测AB卷》必修一 专题八 函数模型与应用 A卷
【题文】某工厂从1970年的年产值200万元增加到40年后2010年的1000万元,假设每年产值增长率相同,则每年年产值增长率是(
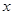
为很小的正数时,
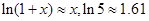
)
题号:767122
题型:选择题
难易度:一般
日期:2016-03-17
来源:《2018-2019学年同步单元双基双测AB卷》必修一 专题八 函数模型与应用 A卷
【题文】甲、乙两种商品在过去一段时间内的价格走势如图所示.假设某人持有资金120万元,他可以在t
1至t
4的任意时刻买卖这两种商品,且买卖能够立即成交(其他费用忽略不计).如果他在t
4时刻卖出所有商品,那么他将获得的最大利润是( )
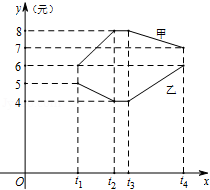
| A.40万元 | B.60万元 | C.120万元 | D.140万元 |
题号:771472
题型:选择题
难易度:较易
日期:2016-03-10
来源:《2018-2019学年同步单元双基双测AB卷》必修一 专题八 函数模型与应用 A卷
【题文】如图所示的是某池塘中的浮萍蔓延的面积(
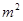
)与时间
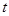
(月)的关系:
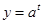
,有以下叙述:
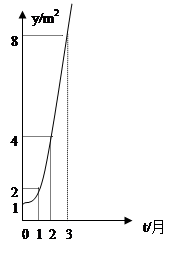
①这个指数函数的底数是2;
②第5个月时,浮萍的面积就会超过
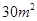
;
③浮萍从
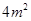
蔓延到
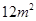
需要经过1.5个月;
④浮萍每个月增加的面积都相等;
⑤若浮萍蔓延到
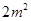
、
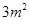
、
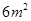
所经过的时间
分别为
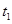
、
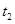
、
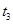
,则
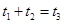
.
其中正确的是 ( )
题号:774294
题型:选择题
难易度:较难
日期:2016-03-04
来源:《2018-2019学年同步单元双基双测AB卷》必修一 专题八 函数模型与应用 A卷
【题文】某地实行阶梯电价,以日历年(每年1月1日至12月31日)为周期执行居民阶梯电价,即:一户居民用户全年不超过2880度(1度=千瓦时)的电量,执行第一档电价标准,每度电0.4883元;全年超过2880度至4800度之间的电量,执行第二档电价标准,每度电0.5383元;全年超过4800度以上的电量,执行第三档电价标准,每度电0.7883元.下面是关于阶梯电价的图形表示,其中正确的有
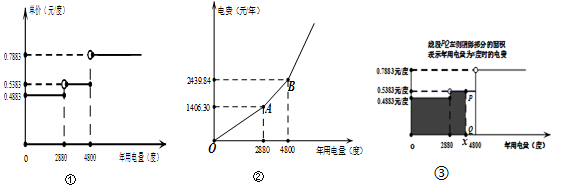
参考数据:0.4883元/度
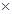
2880度=1406.30元,
0.5383元/度
(4800-2880)度+1406.30元=2439.84元.
题号:778854
题型:选择题
难易度:一般
日期:2016-02-24
来源:《2018-2019学年同步单元双基双测AB卷》必修一 专题八 函数模型与应用 A卷
【题文】某市的房价(均价)经过6年时间从1200元/m
2增加到了4800元/m
2,则这6年间平均每年的增长率是( )
| A.600元 | B.50﹪ | C.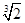 -1 -1 | D.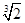 +1. +1. |
题号:3677198
题型:选择题
难易度:容易
日期:2017-05-19
来源:《2018-2019学年同步单元双基双测AB卷》必修一 专题八 函数模型与应用 A卷
【题文】甲、乙、丙.丁四辆玩具赛车同时从起点出发并做匀速直线运动,丙车最先到达终点.丁车最后到达终点.若甲、乙两车的
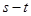
图象如图所示,则对于丙、丁两车的图象所在区域,判断正确的是( )
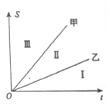
| A.丙在Ⅲ区域,丁在Ⅰ区域 | B.丙在Ⅰ区城,丁在Ⅲ区域 |
| C.丙在Ⅱ区域,丁在Ⅰ区域 | D.丙在Ⅲ区域,丁在Ⅱ区域 |
题号:741899
题型:填空题
难易度:较易
日期:2016-06-07
来源:《2018-2019学年同步单元双基双测AB卷》必修一 专题八 函数模型与应用 A卷
【题文】某桶装水经营部每天的房租、人员工资等固定成本为
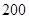
元,每桶水的进价是
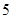
元,销售单价与日均销售量的关系如下表所示.

请根据以上数据分析,这个经营部定价在
元/桶才能获得最大利润.
题号:752648
题型:填空题
难易度:较易
日期:2016-04-29
来源:《2018-2019学年同步单元双基双测AB卷》必修一 专题八 函数模型与应用 A卷
【题文】某食品的保鲜时间y (单位:小时)与储藏温度x (单位:℃)满足函数关系
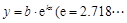
为自然对数的底数,
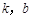
为常数).若该食品在0 ℃时的保鲜时间是100小时,在15 ℃时的保鲜时间是10小时,则该食品在30 ℃时的保鲜时间是__________小时.
题号:774109
题型:填空题
难易度:一般
日期:2016-03-04
来源:《2018-2019学年同步单元双基双测AB卷》必修一 专题八 函数模型与应用 A卷
【题文】某食品的保鲜时间t(单位:小时)与储藏温度x(单位:℃)满足函数关系
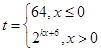
且该食品在4℃的保鲜时间是16小时.
已知甲在某日上午10时购买了该食品,并将其遗放在室外,且此日的室外温度随时间变化如图所示.给出以下四个结论:
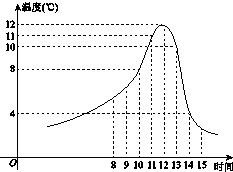
①该食品在6℃的保鲜时间是8小时;
②当x∈[﹣6,6]时,该食品的保鲜时间t随着x增大而逐渐减少;
③到了此日13时,甲所购买的食品还在保鲜时间内;
④到了此日14时,甲所购买的食品已然过了保鲜时间.
其中,所有正确结论的序号是
.
题号:6013236
题型:填空题
难易度:一般
日期:2017-11-26
来源:《2018-2019学年同步单元双基双测AB卷》必修一 专题八 函数模型与应用 A卷
【题文】计算机的价格大约每3年下降
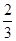
,那么今年花8 100元买的一台计算机,9年后的价格大约是________元.
题号:695358
题型:解答题
难易度:较易
日期:2016-11-17
来源:《2018-2019学年同步单元双基双测AB卷》必修一 专题八 函数模型与应用 A卷
【题文】为了预防流感,某学校对教室用药熏消毒法进行消毒.已知药物释放过程中,室内每立方米空气中的含药量
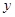
(毫克)与时间
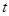
(小时)成正比;药物释放完毕后,
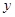
与
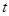
的函数关系式为
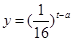
(
为常数),如图所示.据图中提供的信息,回答下列问题:
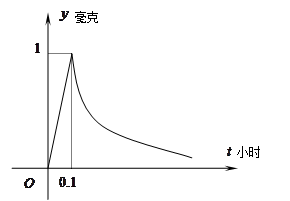
(1)写出从药物释放开始,每立方米空气中的含药量
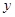
(毫克)与时间
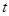
(小时)之间的函数关系式;
(2)据测定,当空气中每立方米的含药量降低到
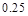
毫克以下时,学生方可进教室。那么药物释放开始,至少需要经过多少小时后,学生才能回到教室?
题号:716631
题型:解答题
难易度:一般
日期:2016-09-06
来源:《2018-2019学年同步单元双基双测AB卷》必修一 专题八 函数模型与应用 A卷
【题文】大学毕业生小王相应国家“自主创业”的号召,利用银行小额无息贷款开办了一家饰品店,该店购进一种今年新上市的饰品进行销售,饰品的进价为每件40元,售价为每件60元,每月可卖出300件,市场调查反映:调整价格时,售价每涨1元每月要少卖10件;售价每下降1元每月多卖20件,为获得更大的利润,现将饰品售价调整为
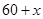
(元/件)(
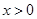
即售价上涨,
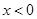
即售价下降),每月饰品销售为
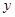
(件),月利润为
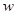
(元).
(1)直接写出
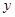
与
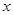
之间的函数关系式;
(2)如何确定销售价格才能使月利润最大?求最大月利润;
(3)为了使每月利润不少于6000元,应如何控制销售价格?
题号:722639
题型:解答题
难易度:一般
日期:2016-08-08
来源:《2018-2019学年同步单元双基双测AB卷》必修一 专题八 函数模型与应用 A卷
【题文】某公司经过测算投资
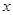
百万元,投资项目
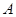
与产生的经济效益
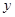
之间满足:
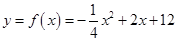
,投资项目
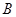
产生的经济效益
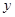
之间满足:
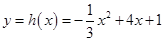
.
(1)现公司共有1千万资金可供投资,应如何分配资金使得投资收益总额最大?
(2)投资边际效应函数
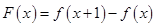
,当边际值小于0时,不建议投资,则应如何分配投资?
题号:726639
题型:解答题
难易度:一般
日期:2016-07-25
来源:《2018-2019学年同步单元双基双测AB卷》必修一 专题八 函数模型与应用 A卷
【题文】某工厂的固定成本为3万元,该工厂每生产100台某产品的生产成本为1万元,设生产该产品
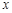
(百台),其总成本为
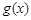
万元(总成本=固定成本+生产成本),并且销售收入
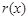
满足
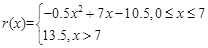
,假设该产品产销平衡,根据上述统计数据规律求:
(Ⅰ)要使工厂有盈利,产品数量
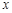
应控制在什么范围?
(Ⅱ)工厂生产多少台产品时盈利最大?
题号:764262
题型:解答题
难易度:一般
日期:2016-03-23
来源:《2018-2019学年同步单元双基双测AB卷》必修一 专题八 函数模型与应用 A卷
【题文】某蔬菜基地种植西红柿,由历年市场行情得知,从二月一日起的300天内,西红柿场售价与上市时间的关系如图一的一条折线表示;西红柿的种植成本与上市时间的关系如图二的抛物线段表示.
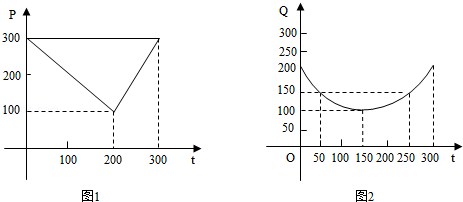
(1)写出图一表示的市场售价与时间的函数关系式p=f(t);写出图二表示的种植成本与时间的函数关系式Q=g(t);
(2)认定市场售价减去种植成本为纯收益,问何时上市的西红柿纯收益最大?(注:市场售价各种植成本的单位:元/10
2㎏,时间单位:天)
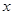 为很小的正数时,
为很小的正数时,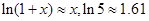 )
)
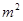 )与时间
)与时间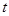 (月)的关系:
(月)的关系: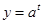 ,有以下叙述:
,有以下叙述: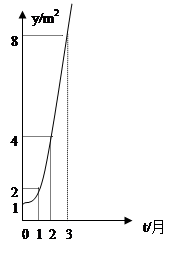
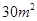 ;
;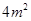 蔓延到
蔓延到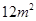 需要经过1.5个月;
需要经过1.5个月;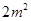 、
、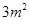 、
、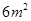 所经过的时间
所经过的时间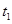 、
、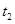 、
、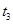 ,则
,则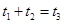 .
.
 2880度=1406.30元,
2880度=1406.30元, (4800-2880)度+1406.30元=2439.84元.
(4800-2880)度+1406.30元=2439.84元.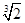 -1
-1 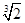 +1.
+1.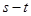 图象如图所示,则对于丙、丁两车的图象所在区域,判断正确的是( )
图象如图所示,则对于丙、丁两车的图象所在区域,判断正确的是( )
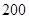 元,每桶水的进价是
元,每桶水的进价是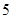 元,销售单价与日均销售量的关系如下表所示.
元,销售单价与日均销售量的关系如下表所示.
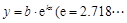 为自然对数的底数,
为自然对数的底数,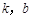 为常数).若该食品在0 ℃时的保鲜时间是100小时,在15 ℃时的保鲜时间是10小时,则该食品在30 ℃时的保鲜时间是__________小时.
为常数).若该食品在0 ℃时的保鲜时间是100小时,在15 ℃时的保鲜时间是10小时,则该食品在30 ℃时的保鲜时间是__________小时.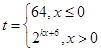 且该食品在4℃的保鲜时间是16小时.
且该食品在4℃的保鲜时间是16小时.
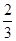 ,那么今年花8 100元买的一台计算机,9年后的价格大约是________元.
,那么今年花8 100元买的一台计算机,9年后的价格大约是________元.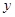 (毫克)与时间
(毫克)与时间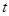 (小时)成正比;药物释放完毕后,
(小时)成正比;药物释放完毕后,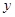 与
与 的函数关系式为
的函数关系式为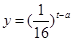 (
(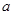 为常数),如图所示.据图中提供的信息,回答下列问题:
为常数),如图所示.据图中提供的信息,回答下列问题: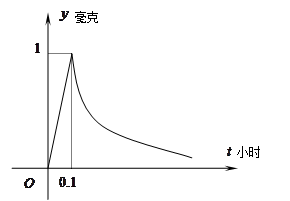
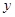 (毫克)与时间
(毫克)与时间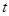 (小时)之间的函数关系式;
(小时)之间的函数关系式;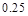 毫克以下时,学生方可进教室。那么药物释放开始,至少需要经过多少小时后,学生才能回到教室?
毫克以下时,学生方可进教室。那么药物释放开始,至少需要经过多少小时后,学生才能回到教室?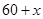 (元/件)(
(元/件)(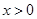 即售价上涨,
即售价上涨,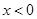 即售价下降),每月饰品销售为
即售价下降),每月饰品销售为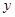 (件),月利润为
(件),月利润为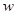 (元).
(元).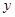 与
与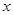 之间的函数关系式;
之间的函数关系式;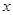 百万元,投资项目
百万元,投资项目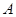 与产生的经济效益
与产生的经济效益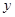 之间满足:
之间满足: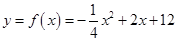 ,投资项目
,投资项目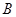 产生的经济效益
产生的经济效益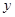 之间满足:
之间满足: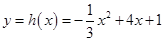 .
.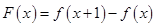 ,当边际值小于0时,不建议投资,则应如何分配投资?
,当边际值小于0时,不建议投资,则应如何分配投资?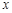 (百台),其总成本为
(百台),其总成本为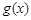 万元(总成本=固定成本+生产成本),并且销售收入
万元(总成本=固定成本+生产成本),并且销售收入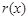 满足
满足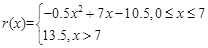 ,假设该产品产销平衡,根据上述统计数据规律求:
,假设该产品产销平衡,根据上述统计数据规律求: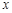 应控制在什么范围?
应控制在什么范围?