适用年级:{{getGradeNameByProperty('高三|专题试卷|全国|2010年')}} 试卷类型:{{getTestPaperTypeName('高三|专题试卷|全国|2010年')}} 使用省份:{{getAreaName('高三|专题试卷|全国|2010年')}}
试卷年份:{{getYear('高三|专题试卷|全国|2010年')}}上传日期:2010-06-25题数:44
提示:单击题文可显示答案与解析。
题号:939610
题型:选择题
难易度:较易
日期:2014-04-06
来源:2010年高考试题分项版理科数学之专题九 立体几何
【题文】在空间,下列命题正确的是
| A.平行直线的平行投影重合 |
| B.平行于同一直线的两个平面平行 |
| C.垂直于同一平面的两个平面平行 |
| D.垂直于同一平面的两条直线平行 |
题号:1084615
题型:选择题
难易度:一般
日期:2012-05-08
来源:2010年高考试题分项版理科数学之专题九 立体几何
【题文】已知正四棱锥
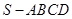
中,
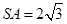
,那么当该棱锥的体积最大时,它的高为
| A.1 | B.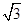 | C.2 | D.3 |
题号:1258289
题型:选择题
难易度:较难
日期:2010-06-23
来源:2010年高考试题分项版理科数学之专题九 立体几何
【题文】正方体
ABCD-
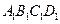
中,
B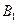
与平面
AC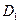
所成角的余弦值为
题号:1262432
题型:选择题
难易度:一般
日期:2010-06-15
来源:2010年高考试题分项版理科数学之专题九 立体几何
【题文】
设
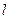
,
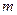
是两条不同的直线,
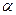
是一个平面,则下列命题正确的是
题号:1262581
题型:选择题
难易度:一般
日期:2010-06-15
来源:2010年高考试题分项版理科数学之专题九 立体几何
【题文】有四根长都为2的直铁条,若再选两根长都为a的直铁条,使这六根铁条端点处相连能够焊接成一个三棱锥形的铁架,则a的取值范围是
题号:1263094
题型:选择题
难易度:较难
日期:2010-06-11
来源:2010年高考试题分项版理科数学之专题九 立体几何
题号:1263095
题型:选择题
难易度:较易
日期:2010-06-11
来源:2010年高考试题分项版理科数学之专题九 立体几何
题号:1264241
题型:选择题
难易度:较难
日期:2010-06-08
来源:2010年高考试题分项版理科数学之专题九 立体几何
【题文】一个几何体的三视图如图,该几何体的表面积为
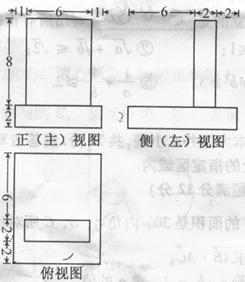
题号:3411194
题型:选择题
难易度:较难
日期:2012-05-29
来源:2010年高考试题分项版理科数学之专题九 立体几何
【题文】已知在半径为2的球面上有
A、
B、
C、
D四点,若
AB=
CD=2,则四面体
ABCD的体积的最大值为
题号:3600624
题型:选择题
难易度:一般
日期:2010-06-10
来源:2010年高考试题分项版理科数学之专题九 立体几何
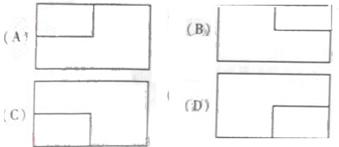
【题文】如图1,△ ABC为三角形,

//
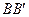
//
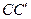
,
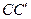
⊥平面ABC 且3

=
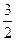
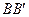
=
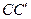
=AB,则多面体△ABC -

的正视图(也称主视图)是
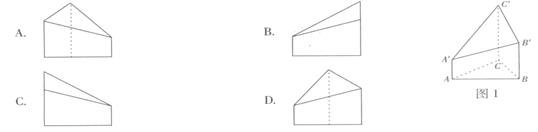
题号:3600852
题型:选择题
难易度:一般
日期:2012-06-18
来源:2010年高考试题分项版理科数学之专题九 立体几何
【题文】与正方体
的三条棱
、
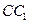
、
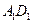
所在直线的距离相等的点
| A.有且只有1个 | B.有且只有2个 |
| C.有且只有3个 | D.有无数个 |
题号:3600857
题型:选择题
难易度:一般
日期:2012-10-16
来源:2010年高考试题分项版理科数学之专题九 立体几何
【题文】设三棱柱的侧棱垂直于底面,所有棱长都为
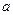
,顶点都在一个球面上,则该球的表面积为
题号:3603247
题型:选择题
难易度:一般
日期:2010-06-18
来源:2010年高考试题分项版理科数学之专题九 立体几何
【题文】半径为
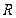
的球
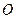
的直径
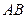
垂直于平面
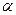
,垂足为
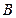
,
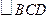
是平面
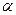
内边长为
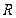
的正三角形,线段
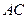
、
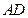
分别
与球面交于点
M,
N,那么
M、
N两点间的球面距离是
(
A)
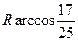
(
B)
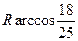
w_w_w.k*s 5*u.c o*m
(
C)
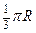
(
D)
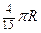
题号:3766550
题型:选择题
难易度:较易
日期:2010-06-10
来源:2010年高考试题分项版理科数学之专题九 立体几何
【题文】如图,若

是长方体ABCD-A
1B
1C
1D
1被平面EFGH截去几何体EFGHB
1C
1后得到的几何体,其中E为线段A
1B
1上异于B
1的点,F为线段BB
1上异于B
1的点,且EH∥A
1 D
1,则下列结论中不正确的是

| A.EH∥FG | B.四边形EFGH是矩形 |
C. 是棱柱 是棱柱 | D. 是棱台 是棱台 |
题号:3767838
题型:选择题
难易度:较易
日期:2010-06-09
来源:2010年高考试题分项版理科数学之专题九 立体几何
【题文】若某空间几何体的三视图如图所示,则该几何体的体积是【】
A. | B.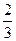 | C.1 | D.2 |
题号:3877111
题型:选择题
难易度:一般
日期:2012-05-22
来源:2010年高考试题分项版理科数学之专题九 立体几何
【题文】到两互相垂直的异面直线的距离相等的点,在过其中一条直线且平行于另一条直线的平面内的轨迹是
题号:3877445
题型:选择题
难易度:一般
日期:2012-05-22
来源:2010年高考试题分项版理科数学之专题九 立体几何
【题文】
过正方体

的顶点
A作直线

,使
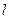
与棱
AB,
AD,
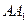
所成的角都相等,这样的直线
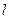
可以作
题号:1262428
题型:填空题
难易度:一般
日期:2010-06-15
来源:2010年高考试题分项版理科数学之专题九 立体几何
【题文】
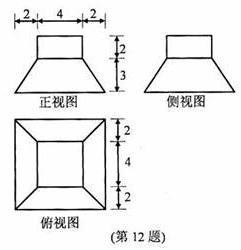
若某几何体的三视图(单位:cm)如图所示,
则此几何体的体积是___________
.
题号:1262605
题型:填空题
难易度:一般
日期:2010-06-13
来源:2010年高考试题分项版理科数学之专题九 立体几何
【题文】一个几何体的三视图如图所示,则这个几何体的体积为
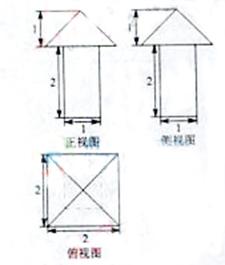
题号:1262769
题型:填空题
难易度:一般
日期:2010-06-13
来源:2010年高考试题分项版理科数学之专题九 立体几何
【题文】正视图为一个三角形的几何体可以是______(写出三种)
题号:3428557
题型:填空题
难易度:一般
日期:2010-06-15
来源:2010年高考试题分项版理科数学之专题九 立体几何
【题文】如图,网格纸的小正方形的边长是1,在其上用粗线画出了某多面体的三视图,则这个多面体最长的一条棱的长为______.
题号:3600854
题型:填空题
难易度:一般
日期:2010-06-17
来源:2010年高考试题分项版理科数学之专题九 立体几何
【题文】已知球
的半径为4,圆
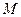
与圆
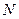
为该球的两个小圆,
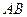
为圆
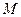
与圆
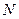
的公共弦,
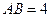
.若
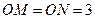
,则两圆圆心的距离
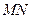
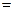
.
题号:3603242
题型:填空题
难易度:一般
日期:2013-03-11
来源:2010年高考试题分项版理科数学之专题九 立体几何
【题文】如图,二面角
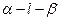
的大小是60°,线段
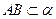
.
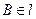
,
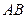
与
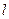
所成的角为30°.则
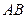
与平面
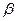
所成的角的正弦值是
.
题号:3766556
题型:填空题
难易度:较易
日期:2010-06-10
来源:2010年高考试题分项版理科数学之专题九 立体几何
【题文】若一个底面是正三角形的三棱柱的正视图如图所示,则其表面积等于( )。
题号:3877446
题型:填空题
难易度:一般
日期:2012-05-22
来源:2010年高考试题分项版理科数学之专题九 立体几何
【题文】
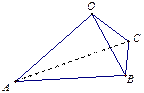
如图,在三棱锥

中,三条棱

,
,

两两垂直,
且
,分别经过三条棱

,
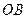
,

作一个截面平
分三棱锥的体积,截面面积依次为
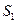
,
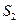
,

,则
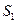
,
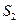
,

的
大小关系为
.
题号:4217132
题型:填空题
难易度:一般
日期:2012-06-05
来源:2010年高考试题分项版理科数学之专题九 立体几何
【题文】圆柱形容器内部盛有高度为8cm的水,若放入三个相同的球(球的半径与圆柱的底面半径相同)后,水恰好淹没最上面的球(如图所示),则球的半径是
cm。

题号:1258281
题型:解答题
难易度:较难
日期:2010-06-23
来源:2010年高考试题分项版理科数学之专题九 立体几何
【题文】(本小题满分12分)(注意:在试题卷上作答无效)
如图,四棱锥
S-
ABCD中,
SD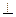
底面
ABCD,
AB//
DC,
AD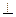 DC
DC,
AB=
AD=1,
DC=
SD=2,
E为棱
SB上的一点,平面
EDC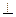
平面
SBC .
(Ⅰ)证明:
SE=2
EB;
(Ⅱ)求二面角
A-
DE-
C的大小 .
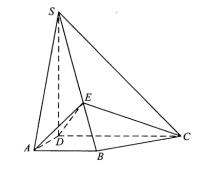
题号:1260969
题型:解答题
难易度:一般
日期:2010-06-18
来源:2010年高考试题分项版理科数学之专题九 立体几何
【题文】如图,在四面体ABOC中,
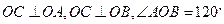
, 且
(Ⅰ)设为
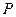
为
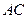
的中点,证明:在
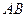
上存在一点
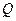
,使
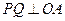
,并计算
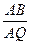
的值;
(Ⅱ)求二面角
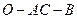
的平面角的余弦值。
题号:1261159
题型:解答题
难易度:一般
日期:2010-06-17
来源:2010年高考试题分项版理科数学之专题九 立体几何
【题文】如图,直三棱柱
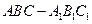
中,
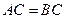
,
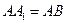
,
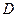
为
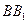
的中点,
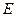
为
上的一点,
.
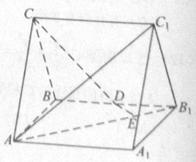
(Ⅰ)证明:
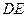
为异面直线
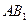
与
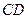
的公垂线;
(Ⅱ)设异面直线
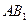
与
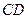
的夹角为45°,求二面角
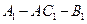
的大小.
题号:1261822
题型:解答题
难易度:一般
日期:2010-06-15
来源:2010年高考试题分项版理科数学之专题九 立体几何
【题文】
如图,

与
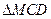
都是边长为2的正三角形,
平面

平面
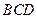
,
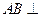
平面
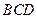
,
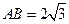
.
(1)求点

到平面

的距离;
(2)求平面
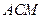
与平面
所成二面角的正弦值.
题号:1262422
题型:解答题
难易度:一般
日期:2010-06-15
来源:2010年高考试题分项版理科数学之专题九 立体几何
【题文】
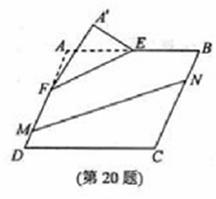
本题满分15分)如图,在矩形
中,点
分别
在线段
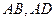
上,
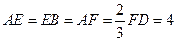
.沿直线
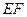
将
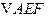
翻折成
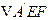
,使平面

.

(Ⅰ)求二面角
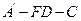
的余弦值;
(Ⅱ)点
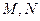
分别在线段
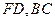
上,若沿直线
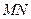
将四
边形
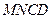
向上翻折,使
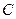
与
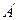
重合,求线段
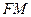
的长。
题号:1262593
题型:解答题
难易度:一般
日期:2010-06-13
来源:2010年高考试题分项版理科数学之专题九 立体几何
【题文】如图,在长方体
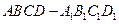
中,
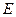
、
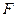
分别是棱
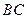
,
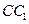
上的点,
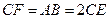
,

(1) 求异面直线
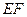
与

所成角的余弦值;
(2) 证明
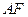
平面

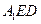
(3) 求二面角
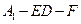
的正弦值。
题号:1263453
题型:解答题
难易度:较易
日期:2010-06-10
来源:2010年高考试题分项版理科数学之专题九 立体几何
【题文】(本小题满分13分)
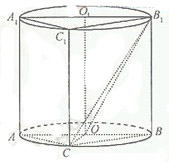
如图,圆柱OO
1内有一个三棱柱ABC-A
1B
1C
1,
三棱柱的底面为圆柱底面的内接三角形,且AB是圆O的直径。
(Ⅰ)证明:平面A
1ACC
1⊥平面B
1BCC
1;
(Ⅱ)设AB=AA
1。在圆柱OO
1内随机选取一点,记该点取自于
三棱柱ABC-A
1B
1C
1内的概率为P。
(i) 当点C在圆周上运动时,求P的最大值;
记平面A
1ACC
1与平面B
1OC所成的角为
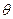
(0°<
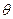
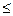
90°)。当P取最大值时,求cos
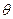
的值。
题号:1263605
题型:解答题
难易度:一般
日期:2010-06-10
来源:2010年高考试题分项版理科数学之专题九 立体几何
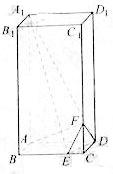
【题文】如图5,
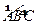
是半径为
a的半圆,
AC为直径,点E为

的中点,点B和点C为线段AD的三等分点.平面AEC外一点F满足
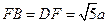
,FE=

a .

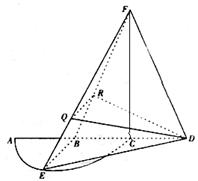
图5
(1)证明:EB⊥FD;
(2)已知点Q,R分别为线段FE,FB上的点,使得

,求平面
与平面

所成二面角的正弦值
题号:1263769
题型:解答题
难易度:较易
日期:2010-06-09
来源:2010年高考试题分项版理科数学之专题九 立体几何
【题文】(本小题满分12分)
如图5所示,在正方体
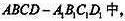
E是棱

的中点。
(Ⅰ)求直线BE的平面

所成的角的正弦值;
(II)在棱
上是否存在一点F,使
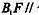
平面

证明你的结论。
题号:1263922
题型:解答题
难易度:较易
日期:2010-06-09
来源:2010年高考试题分项版理科数学之专题九 立体几何
【题文】

题号:1264097
题型:解答题
难易度:较难
日期:2010-06-08
来源:2010年高考试题分项版理科数学之专题九 立体几何
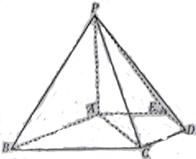
【题文】(本小题满分12分)
如图,在多面体
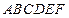
中,四边形
是正方形,
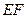
∥
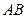
,
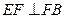
,
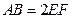
,
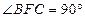
,
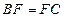
,
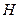
为
的中点。
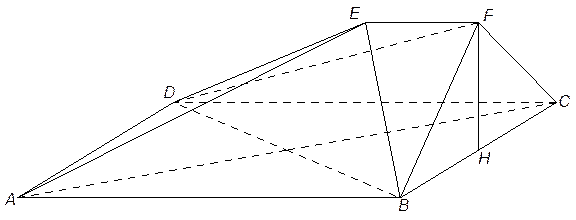
(Ⅰ)求证:
∥平面
;
(Ⅱ)求证:
平面
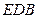
;
(Ⅲ)求二面角
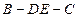
的大小。
题号:1264252
题型:解答题
难易度:较难
日期:2010-06-08
来源:2010年高考试题分项版理科数学之专题九 立体几何
【题文】(14分)如图,四棱锥P-ABCD中,PD⊥平面ABCD,PD=DC=BC=1,AB=2,AB∥DC,∠BCD=90
0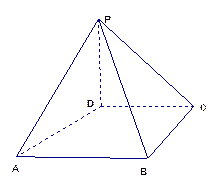
(1)求证:PC⊥BC
(2)求点A到平面PBC的距离
题号:3428553
题型:解答题
难易度:一般
日期:2012-05-22
来源:2010年高考试题分项版理科数学之专题九 立体几何
【题文】已知三棱锥P-ABC中,PA⊥ABC,AB⊥AC,PA=AC=½AB,N为AB上一点,AB=4AN,M,S分别为PB,BC的中点.
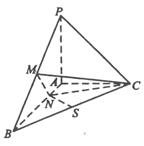
(Ⅰ)证明:CM⊥SN;
(Ⅱ)求SN与平面CMN所成角的大小.
题号:3600859
题型:解答题
难易度:一般
日期:2010-06-13
来源:2010年高考试题分项版理科数学之专题九 立体几何
【题文】如图,已知四棱锥P-ABCD的底面为等腰梯形,AB
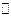
CD,AC
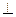
BD,垂足为H,PH是四棱锥的高,E为AD中点
(1) 证明:PE
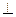
BC
(2) 若
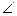
APB=
ADB=60°,求直线PA与平面PEH所成角的正弦值
题号:3603252
题型:解答题
难易度:一般
日期:2010-06-18
来源:2010年高考试题分项版理科数学之专题九 立体几何
【题文】已知正方体
ABCD-
A'
B'
C'
D'的棱长为1,点
M是棱
AA'的中点,点
O是对角线
BD'的中点.
(Ⅰ)求证:
OM为异面直线
AA'和
BD'的公垂线;

(Ⅱ)求二面角
M-
BC'-
B'的大小;
(Ⅲ)求三棱锥
M-
OBC的体积.



w_w w. k#s5_u.c o*m
题号:3760206
题型:解答题
难易度:较难
日期:2010-06-11
来源:2010年高考试题分项版理科数学之专题九 立体几何
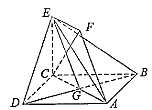
【题文】(本小题共14分)
如图,正方形
ABCD和四边形
ACEF所在的平面互相垂直,
CE⊥AC,EF∥AC,AB=
,
CE=EF=1.(Ⅰ)求证:
AF∥平面
BDE;
(Ⅱ)求证:
CF⊥平面
BDE;(Ⅲ)求二面角
A-BE-D的大小。[来源:学科网ZXXK]
题号:3877113
题型:解答题
难易度:一般
日期:2010-06-17
来源:2010年高考试题分项版理科数学之专题九 立体几何
【题文】如题(19)图,四棱锥P-ABCD中,底面ABCD为矩形,PA
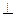
底面ABCD,PA=AB=
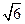
,点E是棱PB的中点。
(I) 求直线AD与平面PBC的距离;
若AD=
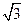
,求二面角A-EC-D的平面角的余弦值。
题号:4217130
题型:解答题
难易度:较易
日期:2013-07-08
来源:2010年高考试题分项版理科数学之专题九 立体几何
【题文】(本小题满分12分)
如图,在五棱锥
P—
ABCDE中,
PA⊥平面
ABCDE,
AB∥
CD,
AC∥
ED,
AE∥
BC,
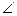 ABC
ABC=45°,
AB=2
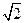
,
BC=2
AE=4,三角形
PAB是等腰三角形.
(Ⅰ)求证:平面
PCD⊥平面
PAC;
(Ⅱ)求直线
PB与平面
PCD所成角的大小;
(Ⅲ)求四棱锥
P—
ACDE的体积.
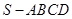 中,
中,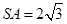 ,那么当该棱锥的体积最大时,它的高为
,那么当该棱锥的体积最大时,它的高为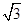
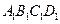 中,B
中,B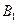 与平面AC
与平面AC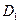 所成角的余弦值为
所成角的余弦值为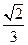
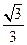
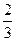
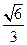
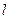 ,
,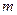 是两条不同的直线,
是两条不同的直线,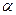 是一个平面,则下列命题正确的是
是一个平面,则下列命题正确的是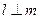 ,
,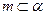 ,则
,则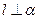
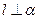 ,
,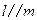 ,则
,则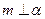
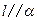 ,
,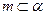 ,则
,则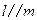
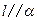 ,
,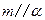 ,则
,则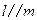
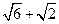 )
)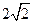 )
)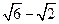 ,
,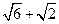 )
)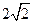 )
) 的棱长为2,动点
的棱长为2,动点 在棱
在棱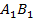 上,动点
上,动点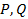 分别在棱
分别在棱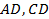 上,若
上,若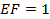 ,
, ,
, ,
,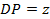 (
(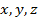 大于零),则四面体
大于零),则四面体 的体积( ).
的体积( ).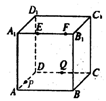
 都有关
都有关 有关,与
有关,与 无关
无关 有关,与
有关,与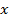 ,
, 无关
无关 有关,与
有关,与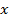 ,
, 无关
无关


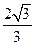
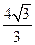
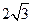
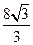
 //
// //
//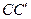 ,
,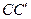 ⊥平面ABC 且3
⊥平面ABC 且3 =
=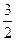
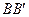 =
=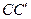 =AB,则多面体△ABC -
=AB,则多面体△ABC - 的正视图(也称主视图)是
的正视图(也称主视图)是
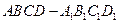 的三条棱
的三条棱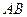 、
、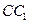 、
、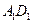 所在直线的距离相等的点
所在直线的距离相等的点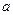 ,顶点都在一个球面上,则该球的表面积为
,顶点都在一个球面上,则该球的表面积为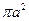
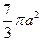
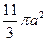
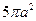
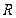 的球
的球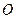 的直径
的直径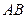 垂直于平面
垂直于平面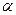 ,垂足为
,垂足为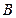 ,
,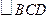 是平面
是平面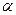 内边长为
内边长为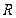 的正三角形,线段
的正三角形,线段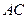 、
、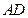 分别
分别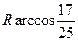 (B)
(B)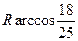 w_w_w.k*s 5*u.c o*m
w_w_w.k*s 5*u.c o*m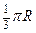 (D)
(D)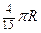
 是长方体ABCD-A1B1C1D1被平面EFGH截去几何体EFGHB1C1后得到的几何体,其中E为线段A1B1上异于B1的点,F为线段BB1上异于B1的点,且EH∥A1 D1,则下列结论中不正确的是
是长方体ABCD-A1B1C1D1被平面EFGH截去几何体EFGHB1C1后得到的几何体,其中E为线段A1B1上异于B1的点,F为线段BB1上异于B1的点,且EH∥A1 D1,则下列结论中不正确的是
 是棱柱
是棱柱 是棱台
是棱台
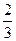
 的顶点A作直线
的顶点A作直线 ,使
,使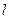 与棱AB,AD,
与棱AB,AD,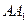
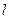 可以作
可以作
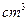 .
.
 的半径为4,圆
的半径为4,圆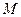 与圆
与圆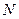 为该球的两个小圆,
为该球的两个小圆,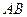 为圆
为圆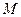 与圆
与圆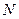 的公共弦,
的公共弦,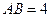 .若
.若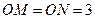 ,则两圆圆心的距离
,则两圆圆心的距离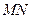
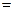 .
.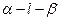 的大小是60°,线段
的大小是60°,线段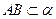 .
.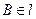 ,
,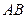 与
与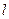 所成的角为30°.则
所成的角为30°.则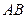 与平面
与平面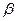 所成的角的正弦值是 .
所成的角的正弦值是 .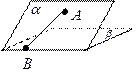

 中,三条棱
中,三条棱 ,
,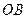 ,
, 两两垂直,
两两垂直,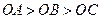 ,分别经过三条棱
,分别经过三条棱 ,
,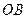 ,
, 作一个截面平
作一个截面平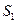 ,
,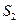 ,
, ,则
,则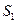 ,
,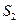 ,
, 的
的
 底面ABCD,AB//DC,AD
底面ABCD,AB//DC,AD DC,AB=AD=1,DC=SD=2,E为棱SB上的一点,平面EDC
DC,AB=AD=1,DC=SD=2,E为棱SB上的一点,平面EDC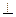 平面SBC .
平面SBC .
 , 且
, 且

 为
为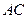 的中点,证明:在
的中点,证明:在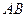 上存在一点
上存在一点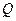 ,使
,使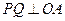 ,并计算
,并计算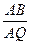 的值;
的值;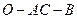 的平面角的余弦值。
的平面角的余弦值。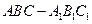 中,
中,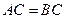 ,
,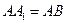 ,
,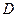 为
为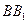 的中点,
的中点,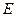 为
为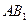 上的一点,
上的一点,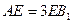 .
.
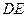 为异面直线
为异面直线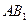 与
与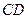 的公垂线;
的公垂线;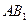 与
与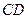 的夹角为45°,求二面角
的夹角为45°,求二面角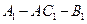 的大小.
的大小. 与
与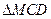 都是边长为2的正三角形,
都是边长为2的正三角形, 平面
平面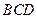 ,
,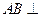 平面
平面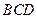 ,
,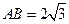 .
. 到平面
到平面 的距离;
的距离; 与平面
与平面 所成二面角的正弦值.
所成二面角的正弦值.
 中,点
中,点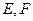 分别
分别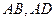 上,
上,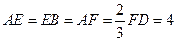 .沿直线
.沿直线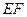
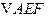 翻折成
翻折成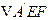 ,使平面
,使平面 .
.
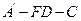 的余弦值;
的余弦值;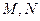 分别在线段
分别在线段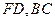 上,若沿直线
上,若沿直线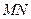 将四
将四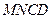 向上翻折,使
向上翻折,使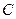 与
与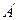 重合,求线段
重合,求线段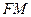
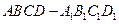 中,
中,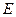 、
、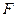 分别是棱
分别是棱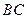 ,
,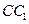

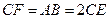 ,
,
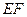 与
与 所成角的余弦值;
所成角的余弦值;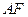
 平面
平面
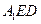
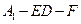 的正弦值。
的正弦值。
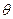 (0°<
(0°< 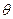
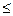 90°)。当P取最大值时,求cos
90°)。当P取最大值时,求cos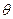 的值。
的值。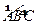 是半径为a的半圆,AC为直径,点E为
是半径为a的半圆,AC为直径,点E为 的中点,点B和点C为线段AD的三等分点.平面AEC外一点F满足
的中点,点B和点C为线段AD的三等分点.平面AEC外一点F满足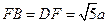 ,FE=
,FE= a .
a .

 ,求平面
,求平面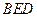 与平面
与平面 所成二面角的正弦值
所成二面角的正弦值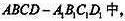 E是棱
E是棱 的中点。
的中点。 所成的角的正弦值;
所成的角的正弦值;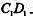 上是否存在一点F,使
上是否存在一点F,使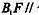 平面
平面 证明你的结论。
证明你的结论。

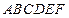 中,四边形
中,四边形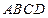 是正方形,
是正方形,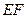 ∥
∥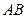 ,
,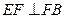 ,
,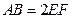 ,
,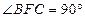 ,
,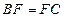 ,
, 为
为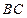 的中点。
的中点。
 ∥平面
∥平面 ;
;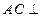 平面
平面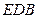 ;
;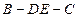 的大小。
的大小。

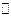 CD,AC
CD,AC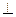 BD,垂足为H,PH是四棱锥的高,E为AD中点
BD,垂足为H,PH是四棱锥的高,E为AD中点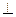 BC
BC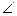 APB=
APB=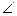 ADB=60°,求直线PA与平面PEH所成角的正弦值
ADB=60°,求直线PA与平面PEH所成角的正弦值 (Ⅱ)求二面角M-BC'-B'的大小;
(Ⅱ)求二面角M-BC'-B'的大小;

 w_w w. k#s5_u.c o*m
w_w w. k#s5_u.c o*m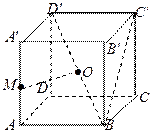
 ,CE=EF=1.
,CE=EF=1.
 底面ABCD,PA=AB=
底面ABCD,PA=AB= ,点E是棱PB的中点。
,点E是棱PB的中点。 ,求二面角A-EC-D的平面角的余弦值。
,求二面角A-EC-D的平面角的余弦值。 ABC=45°,AB=2
ABC=45°,AB=2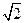 ,BC=2AE=4,三角形PAB是等腰三角形.
,BC=2AE=4,三角形PAB是等腰三角形.