适用年级:{{getGradeNameByProperty('高三|专题试卷|全国|2014年')}} 试卷类型:{{getTestPaperTypeName('高三|专题试卷|全国|2014年')}} 使用省份:{{getAreaName('高三|专题试卷|全国|2014年')}}
试卷年份:{{getYear('高三|专题试卷|全国|2014年')}}上传日期:2014-03-16题数:11
提示:单击题文可显示答案与解析。
题号:948766
题型:选择题
难易度:一般
日期:2014-03-16
来源:2014年高考数学(理)二轮复习专题提升训练优化重组卷1练习卷(带解析)
【题文】记△
ABC各边的中点分别为
D,
E,
F,在
A,
B,
C,
D,
E,
F中任取4点,若这4点为平行四边形顶点,则称为选取成功.某人连续进行3次这种选取,则至少成功1次的概率是( ).
题号:948767
题型:选择题
难易度:一般
日期:2014-03-16
来源:2014年高考数学(理)二轮复习专题提升训练优化重组卷1练习卷(带解析)
【题文】已知随机变量
X~
N(1,4)且
P(
X<2)=0.72,则
P(1<
X<2)等于( ).
| A.0.36 | B.0.16 | C.0.22 | D.0.28 |
题号:948768
题型:选择题
难易度:一般
日期:2014-03-16
来源:2014年高考数学(理)二轮复习专题提升训练优化重组卷1练习卷(带解析)
【题文】甲射击命中目标的概率是
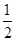
,乙命中目标的概率是
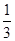
,丙命中目标的概率是
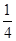
.现在三人同时射击目标,则目标被击中的概率为( ).
题号:4187803
题型:选择题
难易度:较易
日期:2014-03-20
来源:2014年高考数学(理)二轮复习专题提升训练优化重组卷1练习卷(带解析)
【题文】设
m为正整数,(
x+
y)
2m展开式的二项式系数的最大值为
a,(
x+
y)
2m+1展开式的二项式系数的最大值为
b,若13
a=7
b,则
m等于( ).
题号:4187804
题型:选择题
难易度:一般
日期:2014-03-20
来源:2014年高考数学(理)二轮复习专题提升训练优化重组卷1练习卷(带解析)
【题文】用0,1,…,9十个数字,可以组成有重复数字的三位数的个数为( ).
题号:948763
题型:填空题
难易度:较易
日期:2014-03-16
来源:2014年高考数学(理)二轮复习专题提升训练优化重组卷1练习卷(带解析)
【题文】小王参加人才招聘会,分别向
A,
B两个公司投递个人简历.假定小王得到
A公司面试的概率为
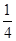
,得到
B公司面试的概率为
p,且两个公司是否让其面试是独立的,记
X为小王得到面试的公司个数.若
X=0时的概率
P(
X=0)=
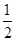
,则随机变量
X的数学期望为________.
题号:948764
题型:填空题
难易度:较易
日期:2014-03-16
来源:2014年高考数学(理)二轮复习专题提升训练优化重组卷1练习卷(带解析)
【题文】一出租车司机从饭店到火车站的途中经过六个交通岗,假设他在各交通岗遇到红灯这一事件是相互独立的,并且概率都是
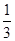
.那么这位司机遇到红灯前,已经通过了两个交通岗的概率是________.
题号:948765
题型:填空题
难易度:一般
日期:2014-03-16
来源:2014年高考数学(理)二轮复习专题提升训练优化重组卷1练习卷(带解析)
【题文】已知正态分布总体落在区间(-∞,0.3)的概率为0.5,那么相应的正态曲线φμ,σ(x)在x=________时达到最高点.
题号:948762
题型:解答题
难易度:较难
日期:2014-03-16
来源:2014年高考数学(理)二轮复习专题提升训练优化重组卷1练习卷(带解析)
【题文】某商场为吸引顾客消费推出一项促销活动,促销规则如下:到该商场购物消费满100元就可转动如图所示的转盘一次,进行抽奖(转盘为十二等分的圆盘),满200元转两次,以此类推;在转动过程中,假定指针停在转盘的任一位置都是等可能的;若转盘的指针落在
A区域,则顾客中一等奖,获得10元奖金;若转盘落在
B区域或
C区域,则顾客中二等奖,获得5元奖金;若转盘指针落在其他区域,则不中奖(若指针停到两区间的实线处,则重新转动).若顾客在一次消费中多次中奖,则对其奖励进行累加.已知顾客甲到该商场购物消费了268元,并按照规则参与了促销活动.
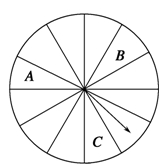
(1)求顾客甲中一等奖的概率;
(2)记
X为顾客甲所得的奖金数,求
X的分布列及其数学期望.
题号:4187805
题型:解答题
难易度:一般
日期:2014-03-20
来源:2014年高考数学(理)二轮复习专题提升训练优化重组卷1练习卷(带解析)
【题文】学校游园活动有这样一个游戏项目:甲箱子里装有3个白球,2个黑球,乙箱子里装有1个白球,2个黑球,这些球除颜色外完全相同.每次游戏从这两个箱子里各随机摸出2个球,若摸出的白球不少于2个,则获奖(每次游戏结束后将球放回原箱).
(1)求在1次游戏中:
①摸出3个白球的概率;②获奖的概率.
(2)求在两次游戏中获奖次数X的分布列及数学期望E(X).
题号:4187806
题型:解答题
难易度:较难
日期:2014-03-20
来源:2014年高考数学(理)二轮复习专题提升训练优化重组卷1练习卷(带解析)
【题文】经销商经销某种农产品,在一个销售季度内,每售出1 t该产品获利润500元,未售出的产品,每1 t亏损300元.根据历史资料,得到销售季度内市场需求量的频率分布直方图,如图所示.经销商为下一个销售季度购进了130 t该农产品.以
X(单位:t,100≤
X≤150)表示下一个销售季度内的市场需求量,
T(单位:元)表示下一个销售季度内经销该农产品的利润.
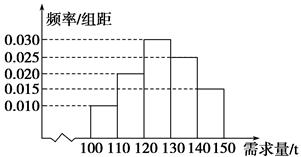
(1)将
T表示为
X的函数;
(2)根据直方图估计利润
T不少于57 000元的概率;
(3)在直方图的需求量分组中,以各组的区间中点值代表该组的各个值,并以需求量落入该区间的频率作为需求量取该区间中点值的概率(例如:若需求量
X∈[100,110),则取
X=105,且
X=105的概率等于需求量落入[100,110)的频率),求
T的数学期望.
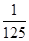
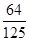
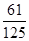
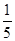
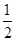 ,乙命中目标的概率是
,乙命中目标的概率是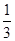 ,丙命中目标的概率是
,丙命中目标的概率是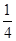 .现在三人同时射击目标,则目标被击中的概率为( ).
.现在三人同时射击目标,则目标被击中的概率为( ).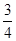
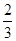
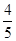
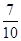
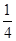 ,得到B公司面试的概率为p,且两个公司是否让其面试是独立的,记X为小王得到面试的公司个数.若X=0时的概率P(X=0)=
,得到B公司面试的概率为p,且两个公司是否让其面试是独立的,记X为小王得到面试的公司个数.若X=0时的概率P(X=0)=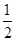 ,则随机变量X的数学期望为________.
,则随机变量X的数学期望为________.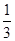 .那么这位司机遇到红灯前,已经通过了两个交通岗的概率是________.
.那么这位司机遇到红灯前,已经通过了两个交通岗的概率是________.
