适用年级:{{getGradeNameByProperty('高三|专题试卷|全国|2014年')}} 试卷类型:{{getTestPaperTypeName('高三|专题试卷|全国|2014年')}} 使用省份:{{getAreaName('高三|专题试卷|全国|2014年')}}
试卷年份:{{getYear('高三|专题试卷|全国|2014年')}}上传日期:2014-03-16题数:11
提示:单击题文可显示答案与解析。
题号:948862
题型:选择题
难易度:较易
日期:2014-03-16
来源:2014年高考数学(理)二轮复习专题提升训练训练11练习卷(带解析)
题号:948864
题型:选择题
难易度:一般
日期:2014-03-16
来源:2014年高考数学(理)二轮复习专题提升训练训练11练习卷(带解析)
题号:948865
题型:选择题
难易度:一般
日期:2014-03-16
来源:2014年高考数学(理)二轮复习专题提升训练训练11练习卷(带解析)
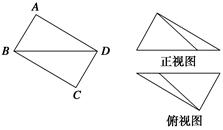
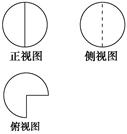
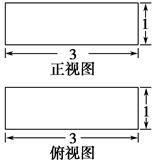
【题文】如图,在矩形
ABCD中,
AB=2,
BC=3,沿
BD将矩形
ABCD折叠,连接
AC,所得三棱锥
A
BCD正视图和俯视图如图,则三棱锥
A
BCD侧视图的面积为( ).
题号:948866
题型:选择题
难易度:一般
日期:2014-03-16
来源:2014年高考数学(理)二轮复习专题提升训练训练11练习卷(带解析)
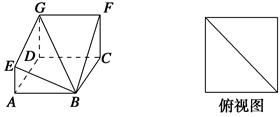
【题文】如图,多面体
ABCD
EFG的底面
ABCD为正方形,
FC=
GD=2
EA,其俯视图如下,则其正视图和侧视图正确的是( ).
题号:3915658
题型:选择题
难易度:一般
日期:2017-07-27
来源:2014年高考数学(理)二轮复习专题提升训练训练11练习卷(带解析)
题号:948861
题型:填空题
难易度:较易
日期:2014-03-16
来源:2014年高考数学(理)二轮复习专题提升训练训练11练习卷(带解析)
【题文】已知三棱锥SABC的所有顶点都在球O的球面上,△ABC是边长为1的正三角形,SC为球O的直径,且SC=2,则此三棱锥的体积为________.
题号:4187853
题型:填空题
难易度:较易
日期:2014-03-20
来源:2014年高考数学(理)二轮复习专题提升训练训练11练习卷(带解析)
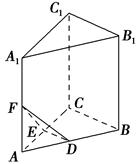
【题文】如图,在三棱柱
A1B1C1
ABC中,
D,
E,
F分别是
AB,
AC,
AA1的中点,设三棱锥
F
ADE的体积为
V1,三棱柱
A1B1C1
ABC的体积为
V2,则
V1∶
V2=________.
题号:4187854
题型:填空题
难易度:较易
日期:2014-03-20
来源:2014年高考数学(理)二轮复习专题提升训练训练11练习卷(带解析)
【题文】一个半径为2的球体经过切割后,剩余部分几何体的三视图如图所示,则该几何体的表面积为________.
题号:948859
题型:解答题
难易度:一般
日期:2014-03-16
来源:2014年高考数学(理)二轮复习专题提升训练训练11练习卷(带解析)
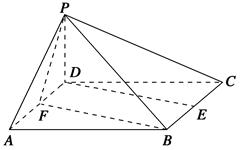
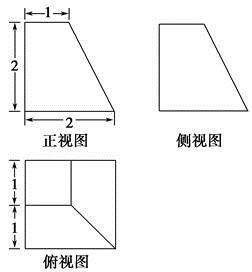
【题文】已知四棱锥
P
ABCD的底面
ABCD是边长为2的正方形,
PD⊥底面
ABCD,
E,
F分别为棱
BC,
AD的中点.
(1)求证:
DE∥平面
PFB;
(2)已知二面角
P
BF
C的余弦值为
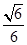
,求四棱锥
P
ABCD的体积.
题号:948860
题型:解答题
难易度:较难
日期:2014-03-16
来源:2014年高考数学(理)二轮复习专题提升训练训练11练习卷(带解析)
【题文】如图,四边形
ABCD是边长为2的正方形,直线
l与平面
ABCD平行,
E和
F是
l上的两个不同点,且
EA=
ED,
FB=
FC.
E′和
F′是平面
ABCD内的两点,
EE′和
FF′都与平面
ABCD垂直.
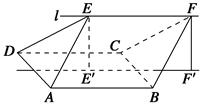
(1)证明:直线
E′
F′垂直且平分线段
AD;
(2)若∠
EAD=∠
EAB=60 °,
EF=2.求多面体
ABCDEF的体积.
题号:4187855
题型:解答题
难易度:较难
日期:2014-03-20
来源:2014年高考数学(理)二轮复习专题提升训练训练11练习卷(带解析)
【题文】已知某几何体的俯视图是如图所示的矩形,正视图是一个底边长为8、高为4的等腰三角形,侧视图是一个底边长为6、高为4的等腰三角形.
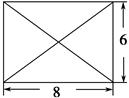
(1)求该几何体的体积
V;
(2)求该几何体的侧面积
S.
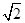
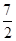 π
π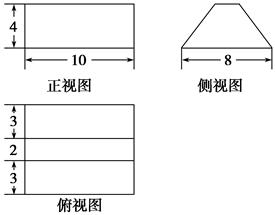
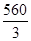
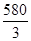

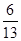
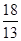
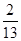
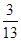


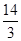
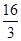



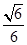 ,求四棱锥PABCD的体积.
,求四棱锥PABCD的体积.
