适用年级:{{getGradeNameByProperty('高三|专题试卷|全国|2014年')}} 试卷类型:{{getTestPaperTypeName('高三|专题试卷|全国|2014年')}} 使用省份:{{getAreaName('高三|专题试卷|全国|2014年')}}
试卷年份:{{getYear('高三|专题试卷|全国|2014年')}}上传日期:2014-03-26题数:14
提示:单击题文可显示答案与解析。
题号:946170
题型:选择题
难易度:一般
日期:2014-03-26
来源:2014年高考数学理复习方案二轮作业手册新课标·通用版专题二练习卷(带解析)
【题文】设函数
f(
x)在R上可导,其导函数为
f′(
x),且函数
y=(2-
x)
f′(
x)的图像如图所示,则下列结论中一定成立的是( )
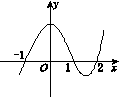
| A.函数f(x)有极大值f(1)和极小值f(-1) |
| B.函数f(x)有极大值f(1)和极小值f(2) |
| C.函数f(x)有极大值f(2)和极小值f(1) |
| D.函数f(x)有极大值f(-1)和极小值f(2) |
题号:946171
题型:选择题
难易度:一般
日期:2014-03-26
来源:2014年高考数学理复习方案二轮作业手册新课标·通用版专题二练习卷(带解析)
【题文】函数
y=
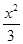
-cos 2
x的图像大致是( )
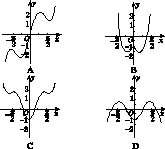
题号:946192
题型:选择题
难易度:较易
日期:2014-03-26
来源:2014年高考数学理复习方案二轮作业手册新课标·通用版专题二练习卷(带解析)
【题文】一个球的体积、表面积分别为
V,
S,若函数
V=
f(
S),
f′(
S)是
f(
S)的导函数,则
f′(π)=( )
A.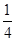 | B.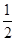 | C.1 | D.π |
题号:946193
题型:选择题
难易度:一般
日期:2014-03-26
来源:2014年高考数学理复习方案二轮作业手册新课标·通用版专题二练习卷(带解析)
【题文】已知函数
f(
x)=
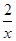
+
xln
x,则曲线
y=
f(
x)在
x=1处的切线方程为( )
| A.x-y-3=0 | B.x-y+3=0 | C.x+y-3=0 | D.x+y+3=0 |
题号:946194
题型:选择题
难易度:较易
日期:2014-03-26
来源:2014年高考数学理复习方案二轮作业手册新课标·通用版专题二练习卷(带解析)
【题文】函数
f(
x)=1-
xlog
2x的零点所在的区间是( )
题号:4187472
题型:选择题
难易度:一般
日期:2014-03-26
来源:2014年高考数学理复习方案二轮作业手册新课标·通用版专题二练习卷(带解析)
【题文】下列函数中,既是偶函数又在区间(0,+∞)上单调递减的是( )
A.y=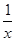 | B.y=e-x | C.y=-x2+1 | D.y=lg |x| |
题号:4187473
题型:选择题
难易度:一般
日期:2014-03-26
来源:2014年高考数学理复习方案二轮作业手册新课标·通用版专题二练习卷(带解析)
【题文】设函数
f(
x)=
x3-4
x+
a(0<
a<2)有三个零点
x1,
x2,
x3,且
x1<
x2<
x3,则下列结论中正确的是( )
| A.x1>-1 | B.x2<0 | C.x3>2 | D.0<x2<1 |
题号:946166
题型:填空题
难易度:一般
日期:2014-03-26
来源:2014年高考数学理复习方案二轮作业手册新课标·通用版专题二练习卷(带解析)
【题文】f(x)=|2x-1|,f1(x)=f(x),f2(x)=f(f1(x)),…,fn(x)=f(fn-1(x)),则函数y=f4(x)的零点个数为________.
题号:946167
题型:填空题
难易度:一般
日期:2014-03-26
来源:2014年高考数学理复习方案二轮作业手册新课标·通用版专题二练习卷(带解析)
【题文】设函数f(x)的定义域为D,若存在非零实数n使得对于任意x∈M(M⊆D),有x+n∈D,且f(x+n)≥f(x),则称f(x)为M上的n高调函数.如果定义域为[-1,+∞)的函数f(x)=x2为[-1,+∞)上的k高调函数,那么实数k的取值范围是________.
题号:946168
题型:填空题
难易度:一般
日期:2014-03-26
来源:2014年高考数学理复习方案二轮作业手册新课标·通用版专题二练习卷(带解析)
【题文】已知函数
f(
x)=
x3+
f′
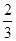 x2
x2-
x,
f(
x)的图像在点
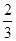
,
f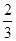
处的切线的斜率是________.
题号:946169
题型:填空题
难易度:较易
日期:2014-03-26
来源:2014年高考数学理复习方案二轮作业手册新课标·通用版专题二练习卷(带解析)
【题文】已知函数
f(
x)=
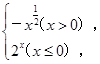
则
f(
f(9))=________.
题号:946164
题型:解答题
难易度:困难
日期:2014-03-26
来源:2014年高考数学理复习方案二轮作业手册新课标·通用版专题二练习卷(带解析)
【题文】已知函数
f(
x)=ln(
x+1)-
x2-
x.
(1)若关于
x的方程
f(
x)=-
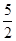 x
x+
b在区间[0,2]上恰有两个不同的实数根,求实数
b的取值范围;
(2)证明:对任意的正整数
n,不等式2+
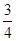
+
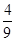
+…+
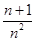
>ln(
n+1)都成立.
题号:946165
题型:解答题
难易度:较难
日期:2014-03-26
来源:2014年高考数学理复习方案二轮作业手册新课标·通用版专题二练习卷(带解析)
【题文】设函数
f(
x)=ln
x+
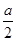 x2
x2-(
a+1)
x(
a>0,
a为常数).
(1)讨论
f(
x)的单调性;
(2)若
a=1,证明:当
x>1时,
f(
x)<
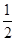 x2
x2-
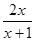
-
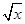
.
题号:4187474
题型:解答题
难易度:一般
日期:2014-03-26
来源:2014年高考数学理复习方案二轮作业手册新课标·通用版专题二练习卷(带解析)
【题文】(13分)某工厂某种产品的年固定成本为250万元,每生产
x千件,需另投入成本
C(
x),当年产量不足80千件时,
C(
x)=
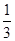 x2
x2+10
x(万元);当年产量不小于80千件时,
C(
x)=51
x+
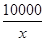
-1 450(万元).每件商品售价为0.05万元.通过市场分析,该厂生产的商品能全部售完.
(1)写出年利润
L(
x)(万元)关于年产量
x(千件)的函数解析式;
(2)年产量为多少千件时,该厂在这一商品的生产中所获利润最大?

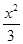 -cos 2x的图像大致是( )
-cos 2x的图像大致是( )
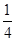
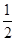
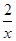 +xln x,则曲线y=f(x)在x=1处的切线方程为( )
+xln x,则曲线y=f(x)在x=1处的切线方程为( )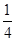 ,
,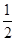
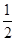 ,1
,1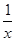
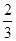 x2-x,f(x)的图像在点
x2-x,f(x)的图像在点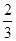 ,f
,f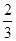 处的切线的斜率是________.
处的切线的斜率是________.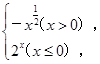 则f(f(9))=________.
则f(f(9))=________. 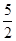 x+b在区间[0,2]上恰有两个不同的实数根,求实数b的取值范围;
x+b在区间[0,2]上恰有两个不同的实数根,求实数b的取值范围;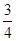 +
+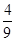 +…+
+…+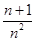 >ln(n+1)都成立.
>ln(n+1)都成立.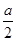 x2-(a+1)x(a>0,a为常数).
x2-(a+1)x(a>0,a为常数).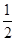 x2-
x2-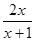 -
-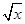 .
.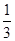 x2+10x(万元);当年产量不小于80千件时,C(x)=51x+
x2+10x(万元);当年产量不小于80千件时,C(x)=51x+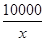 -1 450(万元).每件商品售价为0.05万元.通过市场分析,该厂生产的商品能全部售完.
-1 450(万元).每件商品售价为0.05万元.通过市场分析,该厂生产的商品能全部售完.