适用年级:{{getGradeNameByProperty('高三|专题试卷|全国|2014年')}} 试卷类型:{{getTestPaperTypeName('高三|专题试卷|全国|2014年')}} 使用省份:{{getAreaName('高三|专题试卷|全国|2014年')}}
试卷年份:{{getYear('高三|专题试卷|全国|2014年')}}上传日期:2014-03-16题数:18
提示:单击题文可显示答案与解析。
题号:949007
题型:选择题
难易度:较易
日期:2014-03-16
来源:2014年高考数学(理)二轮复习专题能力测评4练习卷(带解析)
【题文】设曲线
y=
xn+1(
n∈N
*)在点(1,1)处的切线与
x轴的交点的横坐标为
xn,则
x1·
x2·…·
xn等于 ( ).
题号:949008
题型:选择题
难易度:一般
日期:2014-03-16
来源:2014年高考数学(理)二轮复习专题能力测评4练习卷(带解析)
【题文】已知公差不为0的等差数列{
an}满足
a1,
a3,
a4成等比数列,
Sn为数列{
an}的前
n项和,则
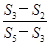
的值为 ( ).
| A.2 | B.3 | C.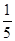 | D.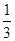 |
题号:949009
题型:选择题
难易度:较难
日期:2014-03-16
来源:2014年高考数学(理)二轮复习专题能力测评4练习卷(带解析)
【题文】已知数列{
an}的前
n项和为
Sn,
a1=1,
Sn=2
an+1,则
Sn=( ).
题号:949010
题型:选择题
难易度:一般
日期:2014-03-16
来源:2014年高考数学(理)二轮复习专题能力测评4练习卷(带解析)
【题文】在数列{
an}中,
a1=1,
a2=2,且
an+2-
an=1+(-1)
n(
n∈N
*),则
S10=( ).
| A.2100 | B.2600 | C.2800 | D.3100 |
题号:949011
题型:选择题
难易度:较易
日期:2014-03-16
来源:2014年高考数学(理)二轮复习专题能力测评4练习卷(带解析)
【题文】已知数列{
an}满足:
a1=1,
an>0,
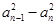
=1(
n∈N
*),那么使
an<5成立的
n的最大值为 ( ).
题号:949032
题型:选择题
难易度:一般
日期:2014-03-16
来源:2014年高考数学(理)二轮复习专题能力测评4练习卷(带解析)
【题文】已知数列{
an}为等比数列,且
a1=4,公比为
q,前
n项和为
Sn,若数列{
Sn+2}也是等比数列,则
q= ( ).
题号:949033
题型:选择题
难易度:较难
日期:2014-03-16
来源:2014年高考数学(理)二轮复习专题能力测评4练习卷(带解析)
【题文】已知等差数列{a
n},若点(n,a
n)(n∈N
*)在经过点(5,3)的定直线l
1上,则数列{a
n}的前9项和S
9=( ).
题号:949034
题型:选择题
难易度:一般
日期:2014-03-16
来源:2014年高考数学(理)二轮复习专题能力测评4练习卷(带解析)
【题文】下面是关于公差
d>0的等差数列{
an}的四个命题:
p1:数列{
an}是递增数列;
p2:数列{
nan}是递增数列;
p3:数列
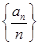
是递增数列;
p4:数列{
an+3
nd}是递增数列.其中的真命题为( ).
| A.p1,p2 | B.p3,p4 | C.p2,p3 | D.p1,p4 |
题号:949035
题型:选择题
难易度:较易
日期:2014-03-16
来源:2014年高考数学(理)二轮复习专题能力测评4练习卷(带解析)
【题文】公比为2的等比数列{
an}的各项都是正数,且
a3a11=16,则
a5=( )
题号:3428474
题型:选择题
难易度:一般
日期:2014-03-17
来源:2014年高考数学(理)二轮复习专题能力测评4练习卷(带解析)
【题文】已知等比数列{
an}的公比为
q,记
bn=
am(n-1)+1+
am(n-1)+2+…+
am(n-1)+m,
cn=
am(n-1)+1·
am(n-1)+2·…·
am(n-1)+m(
m,
n∈N
*),则以下结论一定正确的是( ).
| A.数列{bn}为等差数列,公差为qm |
| B.数列{bn}为等比数列,公比为q2m |
| C.数列{cn}为等比数列,公比为qm2 |
| D.数列{cn}为等比数列,公比为qmn |
题号:942745
题型:填空题
难易度:一般
日期:2014-03-31
来源:2014年高考数学(理)二轮复习专题能力测评4练习卷(带解析)
【题文】在等差数列{an}中,已知a3+a8=10,则3a5+a7=________.
题号:949004
题型:填空题
难易度:一般
日期:2014-03-16
来源:2014年高考数学(理)二轮复习专题能力测评4练习卷(带解析)
【题文】对于正项数列{
an},定义
Hn=
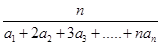
为{
an}的“光阴”值,现知某数列的“光阴”值为
Hn=
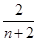
,则数列{
an}的通项公式为________.
题号:949005
题型:填空题
难易度:一般
日期:2014-03-16
来源:2014年高考数学(理)二轮复习专题能力测评4练习卷(带解析)
【题文】若等比数列{an}满足a2+a4=20,a3+a5=40,则数列{an}的前n项和Sn=________.
题号:4187890
题型:填空题
难易度:一般
日期:2014-03-17
来源:2014年高考数学(理)二轮复习专题能力测评4练习卷(带解析)
【题文】已知△ABC的一个内角为120°,并且三边长构成公差为4的等差数列,则△ABC的面积为________.
题号:949000
题型:解答题
难易度:较难
日期:2014-03-16
来源:2014年高考数学(理)二轮复习专题能力测评4练习卷(带解析)
【题文】已知单调递增的等比数列{
an}满足:
a2+
a3+
a4=28,且
a3+2是
a2和
a4的等差中项.
(1)求数列{
an}的通项公式
an;
(2)令
bn=
anlog
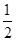 an
an,
Sn=
b1+
b2+…+
bn,求使
Sn+
n·2
n+1>50成立的最小的正整数
n.
题号:949001
题型:解答题
难易度:较难
日期:2014-03-16
来源:2014年高考数学(理)二轮复习专题能力测评4练习卷(带解析)
【题文】设数列{
an}满足
a1=2,
a2+
a4=8,且对任意
n∈N
*,函数
f(
x)=(
an-
an+1+
an+2)
x+
an+1cos
x-
an+2sin
x满足
f′
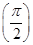
=0.
(1)求数列{
an}的通项公式;
(2)若
bn=2
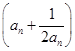
,求数列{
bn}的前
n项和
Sn.
题号:949002
题型:解答题
难易度:较难
日期:2014-03-16
来源:2014年高考数学(理)二轮复习专题能力测评4练习卷(带解析)
【题文】设数列{an}的前n项和为Sn,数列{Sn}的前n项和为Tn,满足Tn=2Sn-n2,n∈N*.
(1)求a1的值;
(2)求数列{an}的通项公式.
题号:949003
题型:解答题
难易度:一般
日期:2014-03-16
来源:2014年高考数学(理)二轮复习专题能力测评4练习卷(带解析)
【题文】在公差为d的等差数列{an}中,已知
a1=10,且a1,2a2+2,5a3成等比数列.
(1)求d,an;
(2)若d<0,求|a1|+|a2|+…+|an|.
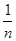
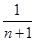
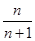
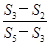 的值为 ( ).
的值为 ( ).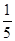
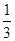
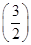 n-1
n-1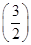 n-1
n-1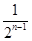
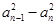 =1(n∈N*),那么使an<5成立的n的最大值为 ( ).
=1(n∈N*),那么使an<5成立的n的最大值为 ( ).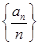 是递增数列;
是递增数列;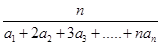 为{an}的“光阴”值,现知某数列的“光阴”值为Hn=
为{an}的“光阴”值,现知某数列的“光阴”值为Hn=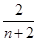 ,则数列{an}的通项公式为________.
,则数列{an}的通项公式为________.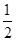 an,Sn=b1+b2+…+bn,求使Sn+n·2n+1>50成立的最小的正整数n.
an,Sn=b1+b2+…+bn,求使Sn+n·2n+1>50成立的最小的正整数n.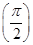 =0.
=0.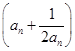 ,求数列{bn}的前n项和Sn.
,求数列{bn}的前n项和Sn.