适用年级:{{getGradeNameByProperty('高三|专题试卷|全国|2014年')}} 试卷类型:{{getTestPaperTypeName('高三|专题试卷|全国|2014年')}} 使用省份:{{getAreaName('高三|专题试卷|全国|2014年')}}
试卷年份:{{getYear('高三|专题试卷|全国|2014年')}}上传日期:2014-03-11题数:10
提示:单击题文可显示答案与解析。
题号:951029
题型:选择题
难易度:一般
日期:2014-03-11
来源:2014年高考数学(理)二轮复习5-2空间向量与立体几何练习卷(带解析)
【题文】如图所示,正方体
ABCD-A1B1C1D1的棱长为1,线段
B1D1上有两个动点
E,
F且
EF=
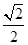
,则下列结论中错误的是 ( ).
| A.AC⊥BE |
| B.EF∥平面ABCD |
| C.三棱锥A-BEF的体积为定值 |
| D.异面直线AE,BF所成的角为定值 |
题号:951030
题型:选择题
难易度:一般
日期:2014-03-11
来源:2014年高考数学(理)二轮复习5-2空间向量与立体几何练习卷(带解析)
【题文】在三棱柱
ABC-A1B1C1中,各棱长相等,侧棱垂直于底面,点
D是侧面
BB1C1C的中心,则
AD与平面
BB1C1C所成角的大小是 ( ).
题号:951031
题型:选择题
难易度:一般
日期:2014-03-11
来源:2014年高考数学(理)二轮复习5-2空间向量与立体几何练习卷(带解析)
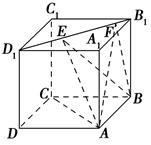
【题文】如图,在直三棱柱ABC-A
1B
1C
1中,∠ACB=90°,AA
1=2,AC=BC=1,则异面直线A
1B与AC所成角的余弦值是().
题号:951052
题型:选择题
难易度:一般
日期:2014-03-11
来源:2014年高考数学(理)二轮复习5-2空间向量与立体几何练习卷(带解析)
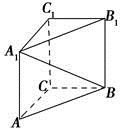
【题文】如图所示,在空间直角坐标系中,有一棱长为
a的正方体
ABC-OA′
B′
C′
D′,
A′
C的中点
E与
AB的中点
F的距离为 ( ).
题号:951053
题型:选择题
难易度:较难
日期:2014-03-11
来源:2014年高考数学(理)二轮复习5-2空间向量与立体几何练习卷(带解析)
【题文】长方体
ABCD-A1B1C1D1中,
AB=
AA1=2,
AD=1,
E为
CC1的中点,则异面直线
BC1与
AE所成角的余弦值为 ( ).
题号:951028
题型:填空题
难易度:较易
日期:2014-03-11
来源:2014年高考数学(理)二轮复习5-2空间向量与立体几何练习卷(带解析)
【题文】如图所示,正方体
ABCD-A1B1C1D1的棱长为
a,
M、
N分别为
A1B和
AC上的点,
A1M=
AN=
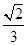 a
a,则
MN与平面
BB1C1C的位置关系是________.
题号:4188148
题型:填空题
难易度:较难
日期:2014-03-11
来源:2014年高考数学(理)二轮复习5-2空间向量与立体几何练习卷(带解析)
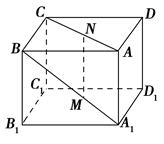
【题文】如图,在棱长为1的正方体
ABCD-A1B1C1D1中,
M和
N分别是
A1B1和
BB1的中点,那么直线
AM与
CN所成角的余弦值为________.
题号:4188149
题型:填空题
难易度:较易
日期:2014-03-11
来源:2014年高考数学(理)二轮复习5-2空间向量与立体几何练习卷(带解析)
【题文】正四棱锥S-ABCD中,O为顶点在底面上的射影,P为侧棱SD的中点,且SO=OD,则直线BC与平面PAC所成的角是________.
题号:951027
题型:解答题
难易度:困难
日期:2014-03-11
来源:2014年高考数学(理)二轮复习5-2空间向量与立体几何练习卷(带解析)
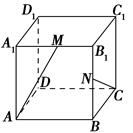
【题文】如图所示的长方体
ABCD-A1B1C1D1中,底面
ABCD是边长为2的正方形,
O为
AC与
BD的交点,
BB1=
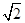
,
M是线段
B1D1的中点.
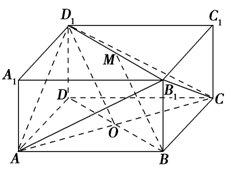
(1)求证:
BM∥平面
D1AC;
(2)求证:
D1O⊥平面
AB1C;
(3)求二面角
B-AB1-
C的大小.
题号:4188150
题型:解答题
难易度:较难
日期:2014-03-11
来源:2014年高考数学(理)二轮复习5-2空间向量与立体几何练习卷(带解析)
【题文】如图,
ABCD是边长为3的正方形,
DE⊥平面
ABCD,
AF∥
DE,
DE=3
AF,
BE与平面
ABCD所成的角为60°.
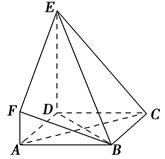
(1)求证:
AC⊥平面
BDE;
(2)求二面角
F-BE-D的余弦值;
(3)设点
M是线段
BD上一个动点,试确定点
M的位置,使得
AM∥平面
BEF,并证明你的结论.
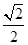 ,则下列结论中错误的是 ( ).
,则下列结论中错误的是 ( ).

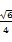
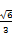
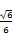
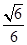

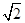 a
a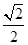 a
a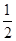 a
a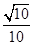
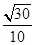
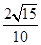
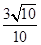
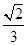 a,则MN与平面BB1C1C的位置关系是________.
a,则MN与平面BB1C1C的位置关系是________.

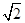 ,M是线段B1D1的中点.
,M是线段B1D1的中点.
