适用年级:{{getGradeNameByProperty('高三|专题试卷|全国|2014年')}} 试卷类型:{{getTestPaperTypeName('高三|专题试卷|全国|2014年')}} 使用省份:{{getAreaName('高三|专题试卷|全国|2014年')}}
试卷年份:{{getYear('高三|专题试卷|全国|2014年')}}上传日期:2014-03-22题数:11
提示:单击题文可显示答案与解析。
题号:947645
题型:填空题
难易度:一般
日期:2014-03-22
来源:2014年高考数学(文)二轮复习专题提升训练江苏专用12练习卷(带解析)
【题文】设椭圆
C∶
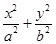
=1(
a>
b>0)恒过定点
A(1,2),则椭圆的中心到准线的距离的最小值________.
题号:947646
题型:填空题
难易度:较难
日期:2014-03-22
来源:2014年高考数学(文)二轮复习专题提升训练江苏专用12练习卷(带解析)
【题文】已知双曲线
C与椭圆
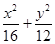
=1有共同的焦点
F1,
F2,且离心率互为倒数.若双曲线右支上一点
P到右焦点
F2的距离为4,则
PF2的中点
M到坐标原点
O的距离等于________.
题号:947647
题型:填空题
难易度:一般
日期:2014-03-22
来源:2014年高考数学(文)二轮复习专题提升训练江苏专用12练习卷(带解析)
【题文】已知双曲线
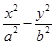
=1(
a>0,
b>0)的一个焦点与抛物线
y2=4
x的焦点重合,且双曲线的离心率等于
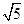
,则该双曲线的方程为________.
题号:947648
题型:填空题
难易度:一般
日期:2014-03-22
来源:2014年高考数学(文)二轮复习专题提升训练江苏专用12练习卷(带解析)
【题文】已知椭圆
E:
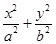
=1(
a>
b>0)的右焦点为
F(3,0),过点
F的直线交椭圆于
A,
B两点.若
AB的中点坐标为(1,-1),则
E的方程为________.
题号:947649
题型:填空题
难易度:一般
日期:2014-03-22
来源:2014年高考数学(文)二轮复习专题提升训练江苏专用12练习卷(带解析)
【题文】已知双曲线
C:
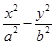
=1(
a>0,
b>0)的右顶点,右焦点分别为
A,
F,它的左准线与
x轴的交点为
B,若
A是线段
BF的中点,则双曲线
C的离心率为________.
题号:947650
题型:填空题
难易度:一般
日期:2014-03-22
来源:2014年高考数学(文)二轮复习专题提升训练江苏专用12练习卷(带解析)
【题文】已知双曲线
C∶
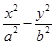
=1(
a>0,
b>0)的实轴长为2,离心率为2,则双曲线
C的焦点坐标是________.
题号:947651
题型:填空题
难易度:较易
日期:2014-03-22
来源:2014年高考数学(文)二轮复习专题提升训练江苏专用12练习卷(带解析)
【题文】双曲线
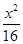
-
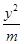
=1(
m>0)的离心率为
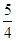
,则
m等于________.
题号:4187623
题型:填空题
难易度:一般
日期:2014-03-23
来源:2014年高考数学(文)二轮复习专题提升训练江苏专用12练习卷(带解析)
【题文】椭圆
T:
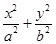
=1(
a>
b>0)的左、右焦点分别为
F1,
F2,焦距为2
c.若直线
y=
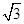
(
x+
c)与椭圆
T的一个交点
M满足∠
MF1F2=2∠
MF2F1,则该椭圆的离心率等于________.
题号:947642
题型:解答题
难易度:较难
日期:2014-03-22
来源:2014年高考数学(文)二轮复习专题提升训练江苏专用12练习卷(带解析)
【题文】在平面直角坐标系
xOy中,过点
A(-2,-1)椭圆
C∶
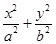
=1(
a>
b>0)的左焦点为
F,短轴端点为
B1、
B2,
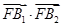
=2
b2.
(1)求
a、
b的值;
(2)过点
A的直线
l与椭圆
C的另一交点为
Q,与
y轴的交点为R.过原点
O且平行于
l的直线与椭圆的一个交点为
P.若
AQ·
AR=3
OP2,求直线
l的方程.
题号:947643
题型:解答题
难易度:较难
日期:2014-03-22
来源:2014年高考数学(文)二轮复习专题提升训练江苏专用12练习卷(带解析)
【题文】已知椭圆
C的中心为平面直角坐标系
xOy的原点,焦点在
x轴上,它的一个顶点到两个焦点的距离分别是7和1.
(1)求椭圆
C的方程;
(2)若
P为椭圆
C上的动点,
M为过
P且垂直于
x轴的直线上的一点,
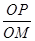
=
λ,求点
M的轨迹方程,并说明轨迹是什么曲线.
题号:947644
题型:解答题
难易度:较难
日期:2014-03-22
来源:2014年高考数学(文)二轮复习专题提升训练江苏专用12练习卷(带解析)
【题文】在平面直角坐标系
xOy中,已知对于任意实数
k,直线(
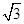 k
k+1)
x+(
k-
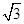
)
y-(3
k+
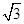
)=0恒过定点
F.设椭圆
C的中心在原点,一个焦点为
F,且椭圆
C上的点到
F的最大距离为2+
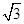
.
(1)求椭圆
C的方程;
(2)设(
m,
n)是椭圆
C上的任意一点,圆
O:
x2+
y2=
r2(
r>0)与椭圆
C有4个相异公共点,试分别判断圆
O与直线
l1:
mx+
ny=1和
l2:
mx+
ny=4的位置关系.
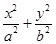 =1(a>b>0)恒过定点A(1,2),则椭圆的中心到准线的距离的最小值________.
=1(a>b>0)恒过定点A(1,2),则椭圆的中心到准线的距离的最小值________.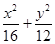 =1有共同的焦点F1,F2,且离心率互为倒数.若双曲线右支上一点P到右焦点F2的距离为4,则PF2的中点M到坐标原点O的距离等于________.
=1有共同的焦点F1,F2,且离心率互为倒数.若双曲线右支上一点P到右焦点F2的距离为4,则PF2的中点M到坐标原点O的距离等于________.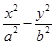 =1(a>0,b>0)的一个焦点与抛物线y2=4x的焦点重合,且双曲线的离心率等于
=1(a>0,b>0)的一个焦点与抛物线y2=4x的焦点重合,且双曲线的离心率等于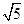 ,则该双曲线的方程为________.
,则该双曲线的方程为________.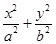 =1(a>b>0)的右焦点为F(3,0),过点F的直线交椭圆于A,B两点.若AB的中点坐标为(1,-1),则E的方程为________.
=1(a>b>0)的右焦点为F(3,0),过点F的直线交椭圆于A,B两点.若AB的中点坐标为(1,-1),则E的方程为________.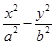 =1(a>0,b>0)的右顶点,右焦点分别为A,F,它的左准线与x轴的交点为B,若A是线段BF的中点,则双曲线C的离心率为________.
=1(a>0,b>0)的右顶点,右焦点分别为A,F,它的左准线与x轴的交点为B,若A是线段BF的中点,则双曲线C的离心率为________.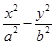 =1(a>0,b>0)的实轴长为2,离心率为2,则双曲线C的焦点坐标是________.
=1(a>0,b>0)的实轴长为2,离心率为2,则双曲线C的焦点坐标是________.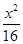 -
-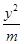 =1(m>0)的离心率为
=1(m>0)的离心率为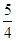 ,则m等于________.
,则m等于________.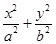 =1(a>b>0)的左、右焦点分别为F1,F2,焦距为2c.若直线y=
=1(a>b>0)的左、右焦点分别为F1,F2,焦距为2c.若直线y=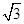 (x+c)与椭圆T的一个交点M满足∠MF1F2=2∠MF2F1,则该椭圆的离心率等于________.
(x+c)与椭圆T的一个交点M满足∠MF1F2=2∠MF2F1,则该椭圆的离心率等于________.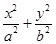 =1(a>b>0)的左焦点为F,短轴端点为B1、B2,
=1(a>b>0)的左焦点为F,短轴端点为B1、B2,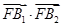 =2b2.
=2b2.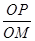 =λ,求点M的轨迹方程,并说明轨迹是什么曲线.
=λ,求点M的轨迹方程,并说明轨迹是什么曲线.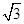 k+1)x+(k-
k+1)x+(k-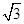 )y-(3k+
)y-(3k+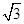 )=0恒过定点F.设椭圆C的中心在原点,一个焦点为F,且椭圆C上的点到F的最大距离为2+
)=0恒过定点F.设椭圆C的中心在原点,一个焦点为F,且椭圆C上的点到F的最大距离为2+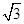 .
.