适用年级:{{getGradeNameByProperty('高三|专题试卷|广东|2010年')}} 试卷类型:{{getTestPaperTypeName('高三|专题试卷|广东|2010年')}} 使用省份:{{getAreaName('高三|专题试卷|广东|2010年')}}
试卷年份:{{getYear('高三|专题试卷|广东|2010年')}}上传日期:2010-12-19题数:20
提示:单击题文可显示答案与解析。
题号:1183407
题型:选择题
难易度:一般
日期:2010-12-19
来源:2011届广东省广州市第86中学高三数学立体几何专题试卷
【题文】设
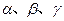
为平面,
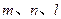
为直线,则
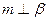
的一个充分条件是 ( )
题号:1183408
题型:选择题
难易度:一般
日期:2010-12-19
来源:2011届广东省广州市第86中学高三数学立体几何专题试卷
题号:3699748
题型:选择题
难易度:一般
日期:2012-12-28
来源:2011届广东省广州市第86中学高三数学立体几何专题试卷
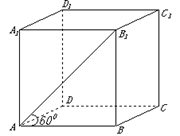
【题文】若正四棱柱
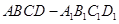
的底面边长为1,
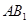
与底面
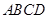
成60°角,则
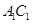
到底面
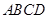
的距离为( )
题号:3877529
题型:选择题
难易度:一般
日期:2012-05-16
来源:2011届广东省广州市第86中学高三数学立体几何专题试卷
【题文】给定下列四个命题:
①若一个平面内的两条直线与另外一个平面都平行,那么这两个平面相互平行;
②若一个平面经过另一个平面的垂线,那么这两个平面相互垂直;
③垂直于同一直线的两条直线相互平行;
④若两个平面垂直,那么一个平面内与它们的交线不垂直的直线与另一个平面也不垂直。
其中,为真命题的是( )
题号:3877530
题型:选择题
难易度:一般
日期:2013-01-21
来源:2011届广东省广州市第86中学高三数学立体几何专题试卷
【题文】已知三棱柱
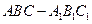
的侧棱与底面边长都相等,
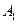
在底面
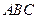
内的射影为
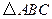
的中心,则
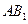
与底面
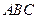
所成角的正弦值等于( )
题号:3877531
题型:选择题
难易度:一般
日期:2010-12-19
来源:2011届广东省广州市第86中学高三数学立体几何专题试卷
题号:3877532
题型:选择题
难易度:一般
日期:2010-12-19
来源:2011届广东省广州市第86中学高三数学立体几何专题试卷
【题文】若正方体的棱长为
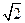
,则以该正方体各个面的中心为顶点的凸多面体的体积为( )
题号:3877533
题型:选择题
难易度:一般
日期:2012-06-18
来源:2011届广东省广州市第86中学高三数学立体几何专题试卷
【题文】对两条不相交的空间直线
a与
b,必存在平面α,使得( )
题号:3877534
题型:选择题
难易度:一般
日期:2013-01-17
来源:2011届广东省广州市第86中学高三数学立体几何专题试卷
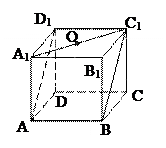
【题文】如图,正方体ABCD-A
1B
1C
1D
1的棱长为1,O是底面
A
1B
1C
1D
1的中心,则O到平面AB C
1D
1的距离为 ( )
题号:3877535
题型:选择题
难易度:一般
日期:2012-07-03
来源:2011届广东省广州市第86中学高三数学立体几何专题试卷
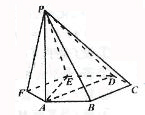
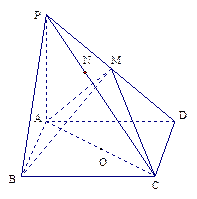
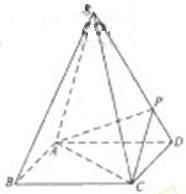
【题文】如图,已知六棱锥
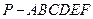
的底面是正六边形,
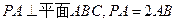
,则下列结论正确的是( )
A.
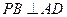
B.平面
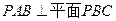
C. 直线
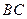
∥平面
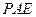
D.
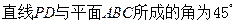
题号:1183404
题型:填空题
难易度:一般
日期:2010-12-19
来源:2011届广东省广州市第86中学高三数学立体几何专题试卷
【题文】已知球O的半径为2,圆
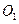
是一小圆,
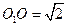
,A、B是圆
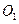
上两点,若A,B两点间的球面距离为
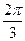
,则
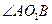
=
.
题号:1183405
题型:填空题
难易度:一般
日期:2010-12-19
来源:2011届广东省广州市第86中学高三数学立体几何专题试卷
【题文】右图是一个几何体的三视图,根据图中数据,
可得该几何体的表面积是
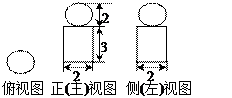
题号:1183406
题型:填空题
难易度:一般
日期:2010-12-19
来源:2011届广东省广州市第86中学高三数学立体几何专题试卷
【题文】若一个球的体积为
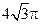
,则它的表面积为
.
题号:3877536
题型:填空题
难易度:一般
日期:2010-12-19
来源:2011届广东省广州市第86中学高三数学立体几何专题试卷
【题文】设
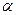
和
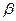
为不重合的两个平面,给出下列命题:
(1)若
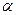
内的两条相交直线分别平行于
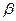
内的两条直线,则
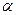
平行于
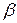
;
(2)若
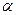
外一条直线
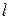
与
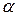
内的一条直线平行,则
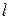
和
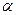
平行;
(3)设
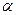
和
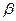
相交于直线
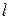
,若
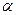
内有一条直线垂直于
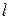
,则
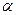
和
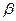
垂直;
(4)直线
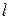
与
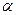
垂直的充分必要条件是
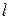
与
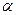
内的两条直线垂直。
上面命题中,真命题的序号
(写出所有真命题的序号).
题号:1183401
题型:解答题
难易度:一般
日期:2010-12-19
来源:2011届广东省广州市第86中学高三数学立体几何专题试卷
【题文】(本小题满分14分)
在长方体ABCD—A
1B
1C
1D
1,中,AD=AA
1=1,AB=2,点E在棱AB上移动.
(1)证明:D
1E⊥A
1D;
(2)当E为AB的中点时,求三棱锥E-ACD
1的体积;
(3)AE等于何值时,二面角D
1—EC—D的大小为
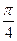
.
题号:1183402
题型:解答题
难易度:一般
日期:2010-12-19
来源:2011届广东省广州市第86中学高三数学立体几何专题试卷
【题文】(本小题满分14分)如图,在三棱锥
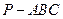
中,
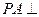
底面

,
点
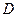
,
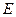
分别在棱
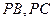
上,且
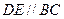


(1)求证:
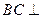
平面
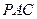
;
(2)当
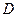
为
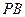
的中点时,求
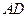
与平面
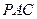
所成的角的正弦值;
(3)是否存在点
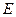
使得二面角
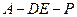
为直二面角?并说明理由.
题号:1183403
题型:解答题
难易度:一般
日期:2010-12-19
来源:2011届广东省广州市第86中学高三数学立体几何专题试卷
【题文】(本小题共14分)在四棱锥
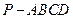
中,底面
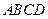
是矩形,
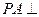
平面
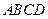
,
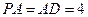
,
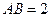
. 以
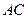
的中点
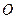
为球心、
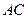
为直径的球面交
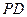
于点
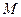
,交
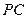
于点
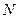
.
(1)求证:平面
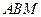
⊥平面
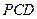
;

(2)求直线
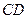
与平面
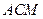
所成的角的正弦值.
题号:3877537
题型:解答题
难易度:一般
日期:2012-10-31
来源:2011届广东省广州市第86中学高三数学立体几何专题试卷
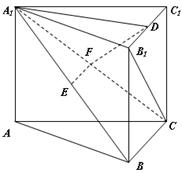
【题文】(本小题满分12分)
如图,在直三棱柱
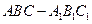
中,
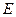
、
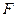
分别是
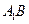
、
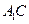
的中点,点
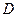
在
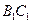
上,
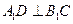
。
求证:(1)EF∥平面ABC;
(2)平面
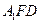
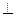
平面
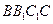
.
题号:3877538
题型:解答题
难易度:一般
日期:2013-02-21
来源:2011届广东省广州市第86中学高三数学立体几何专题试卷
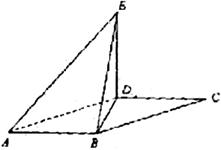
【题文】(本小题满分12分)
如图,平行四边形
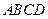
中,
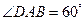
,
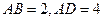
将
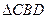
沿
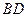
折起到
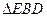
的位置,使平面
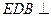
平面
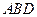
(1)求证:
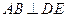
;
(2)求三棱锥
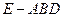
的侧面积.
题号:3877539
题型:解答题
难易度:一般
日期:2010-12-19
来源:2011届广东省广州市第86中学高三数学立体几何专题试卷
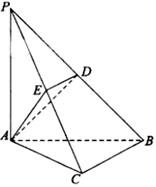
【题文】(本小题满分14分)
如图,四棱锥
S-ABCD的底面是正方形,每条侧棱的长都是底面边长的
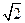
倍,P为侧棱SD上的点。
(1)求证:
AC⊥
SD;
(2)若
SD⊥
平面PAC,求二面角
P-AC-D的大小;
(3)在(2)的条件下,侧棱SC上是否存在一点E,使得BE∥平面PAC。若存在,求SE:EC的值;若不存在,试说明理由。
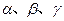 为平面,
为平面,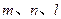 为直线,则
为直线,则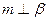 的一个充分条件是 ( )
的一个充分条件是 ( )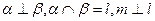
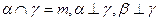
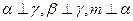
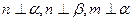
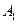
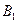
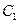
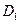 的棱上到异面直线AB,C
的棱上到异面直线AB,C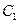 的距离相等的点的个数为( )
的距离相等的点的个数为( )
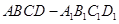 的底面边长为1,
的底面边长为1,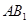 与底面
与底面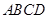 成60°角,则
成60°角,则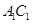 到底面
到底面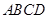 的距离为( )
的距离为( )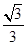
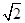

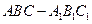 的侧棱与底面边长都相等,
的侧棱与底面边长都相等,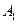 在底面
在底面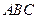 内的射影为
内的射影为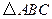 的中心,则
的中心,则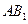 与底面
与底面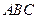 所成角的正弦值等于( )
所成角的正弦值等于( )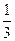
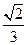
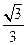
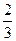
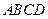 的顶点
的顶点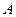 ,
,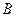 ,
,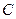 分别在两两垂直的三条射线
分别在两两垂直的三条射线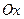 ,
,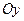 ,
,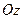 上,则在下列命题中,错误的为( )
上,则在下列命题中,错误的为( )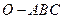 是正三棱锥
是正三棱锥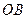 ∥平面
∥平面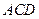
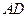 与
与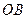 所成的角是
所成的角是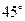
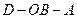 为
为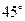

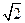 ,则以该正方体各个面的中心为顶点的凸多面体的体积为( )
,则以该正方体各个面的中心为顶点的凸多面体的体积为( ) 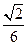
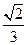
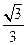
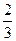 .
. 

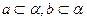
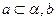 ∥α
∥α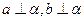
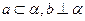
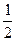
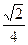
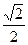
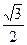

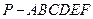 的底面是正六边形,
的底面是正六边形,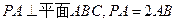 ,则下列结论正确的是( )
,则下列结论正确的是( )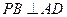 B.平面
B.平面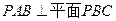
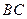 ∥平面
∥平面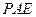 D.
D.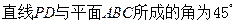

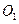 是一小圆,
是一小圆,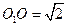 ,A、B是圆
,A、B是圆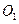 上两点,若A,B两点间的球面距离为
上两点,若A,B两点间的球面距离为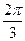 ,则
,则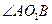 = .
= .
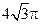 ,则它的表面积为 .
,则它的表面积为 .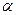 和
和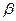 为不重合的两个平面,给出下列命题:
为不重合的两个平面,给出下列命题: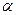 内的两条相交直线分别平行于
内的两条相交直线分别平行于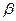 内的两条直线,则
内的两条直线,则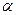 平行于
平行于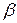 ;
;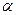 外一条直线
外一条直线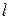 与
与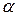 内的一条直线平行,则
内的一条直线平行,则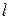 和
和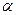 平行;
平行;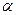 和
和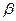 相交于直线
相交于直线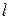 ,若
,若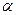 内有一条直线垂直于
内有一条直线垂直于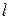 ,则
,则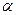 和
和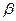 垂直;
垂直;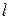 与
与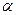 垂直的充分必要条件是
垂直的充分必要条件是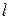 与
与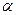 内的两条直线垂直。
内的两条直线垂直。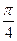 .
. 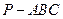 中,
中,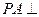 底面
底面 ,
,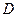 ,
,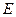 分别在棱
分别在棱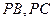 上,且
上,且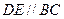


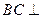 平面
平面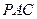 ;
;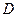 为
为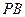 的中点时,求
的中点时,求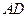 与平面
与平面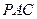 所成的角的正弦值;
所成的角的正弦值;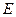 使得二面角
使得二面角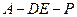 为直二面角?并说明理由.
为直二面角?并说明理由.
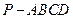 中,底面
中,底面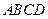 是矩形,
是矩形,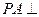 平面
平面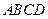 ,
,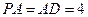 ,
,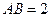 . 以
. 以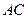 的中点
的中点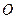 为球心、
为球心、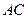 为直径的球面交
为直径的球面交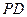 于点
于点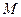 ,交
,交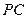 于点
于点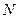 .
.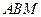 ⊥平面
⊥平面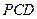 ;
;
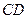 与平面
与平面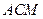 所成的角的正弦值.
所成的角的正弦值.
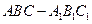 中,
中,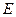 、
、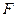 分别是
分别是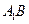 、
、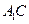 的中点,点
的中点,点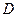 在
在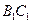 上,
上,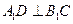 。
。 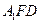
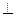 平面
平面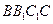 .
.
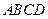 中,
中,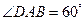 ,
,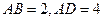 将
将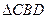 沿
沿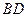 折起到
折起到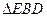 的位置,使平面
的位置,使平面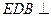 平面
平面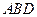
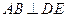 ;
; 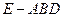 的侧面积.
的侧面积.
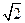 倍,P为侧棱SD上的点。
倍,P为侧棱SD上的点。 