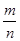适用年级:{{getGradeNameByProperty('初三|同步测试|浙江|2017年')}} 试卷类型:{{getTestPaperTypeName('初三|同步测试|浙江|2017年')}} 使用省份:{{getAreaName('初三|同步测试|浙江|2017年')}}
试卷年份:{{getYear('初三|同步测试|浙江|2017年')}}上传日期:2017-07-29题数:12
提示:单击题文可显示答案与解析。
题号:4763520
题型:单选题
难易度:一般
日期:2017-07-29
来源:九年级数学(浙教版)上册同步练习:2.3 用频率估计概率
【题文】抛掷同一枚啤酒瓶盖1000次,经过统计得“凸面向上”的频率约为0.44,则由此可估计抛掷这枚啤酒瓶盖出现“凹面向上”的概率约为( )
题号:4763521
题型:单选题
难易度:一般
日期:2017-07-29
来源:九年级数学(浙教版)上册同步练习:2.3 用频率估计概率
【题文】在一个不透明的盒子中装有a个除颜色外完全相同的球,这a个球中只有3个红球,若每次将球充分搅匀后,任意摸出1个球记下颜色再放回盒子.通过大量重复试验后,发现摸到红球的频率稳定在20%左右,则a的值约为()
题号:4763522
题型:单选题
难易度:一般
日期:2017-07-29
来源:九年级数学(浙教版)上册同步练习:2.3 用频率估计概率
【题文】下列说法中,正确的个数是( )
①不可能事件发生的概率为0.
②在相同条件下,只要试验的次数足够多,频率就可以作为概率的估计值.
③收集数据过程中的“记录结果”这一步,就是记录每个对象出现的频率.
题号:4763515
题型:填空题
难易度:一般
日期:2017-07-29
来源:九年级数学(浙教版)上册同步练习:2.3 用频率估计概率
【题文】一个口袋里有30个球,其中红球、黑球、黄球若干个,从口袋中随机摸出一球记下其颜色,再把它放回口袋中摇匀,重复上述过程,共试验2000次,其中有1200次摸到黄球,600次摸到红球,由此估计袋中的红球比黑球多__个.
题号:4763516
题型:填空题
难易度:一般
日期:2017-07-29
来源:九年级数学(浙教版)上册同步练习:2.3 用频率估计概率
【题文】一个盒中装有大小、外形一模一样的
x颗白色弹珠和
y颗黑色弹珠,从盒中随机取出一颗弹珠,取得白色弹珠的概率为

.若再往盒中放进12颗同样的白色弹珠,取得白色弹珠的概率是
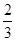
,则原来盒中有白色弹珠__颗.
题号:4763518
题型:填空题
难易度:一般
日期:2017-07-29
来源:九年级数学(浙教版)上册同步练习:2.3 用频率估计概率
【题文】某种油菜籽在相同条件下发芽试验的结果如下表:
每批粒数n
| 100
| 300
| 400
| 600
| 1000
| 2000
| 3000
|
发芽的频数m
| 96
| 284
| 384
| 571
| 948
| 1902
| 2848
|
发芽的频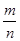
| 0.960
| 0.947
| 0.960
| 0.952
| 0.948
| 0.951
| 0.949
|
那么这种油菜籽发芽的概率约为___(结果精确到0.01).
题号:4763519
题型:填空题
难易度:一般
日期:2017-07-29
来源:九年级数学(浙教版)上册同步练习:2.3 用频率估计概率
【题文】在一个不透明的口袋中,装有12个黄球和若干个红球,这些球除颜色外没有其他区别.小李通过多次摸球试验后发现,从中随机摸出一个红球的频率稳定在25%,则该口袋中红球的个数可能是__ .
题号:4763512
题型:解答题
难易度:一般
日期:2017-07-29
来源:九年级数学(浙教版)上册同步练习:2.3 用频率估计概率
【题文】一粒木质中国象棋棋子“車”,它的正面雕刻一个“車”字,它的反面是平的,将棋子从一定高度下抛,落地反弹后可能是“車”字面朝上,也可能是“車”字面朝下.由于棋子的两面不均匀,为了估计“車”字面朝上的概率,某实验小组做了棋子下抛实验,并把实验数据整理如下:
实验次数
| 20
| 40
| 60
| 80
| 100
| 120
| 140
| 160
|
“車”字面朝上的频数
| 14
| 28
| 38
| 47
| 52
| 66
| 78
| 88
|
相应的频率
| 0.7
| 0.7
| 0.63
| 0.59
| 0.52
| 0.55
| 0.56
| 0.55
|

(1)请将表中数据补充完整,并画出折线统计图中的剩余部分.
(2)如果实验继续进行下去,根据上表数据,这个实验的频率将接近于该事件发生的概率,请估计这个概率是多少?
题号:4763513
题型:解答题
难易度:一般
日期:2017-07-29
来源:九年级数学(浙教版)上册同步练习:2.3 用频率估计概率
【题文】(8分)问题情景:某学校数学学习小组在讨论“随机掷二枚均匀的硬币,得到一正一反的概率是多少”时,小聪说:随机掷二枚均匀的硬币,可以有“二正、一正一反、二反”三种情况,所以,P(一正一反)=
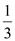
;小颖反驳道:这里的“一正一反”实际上含有“一正一反,一反一正”二种情况,所以P(一正一反)=
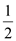
.
⑴
的说法是正确的.
⑵为验证二人的猜想是否正确,小聪与小颖各做了100次实验,得到如下数据:

计算:小聪与小颖二人得到的“一正一反”的频率分别是多少?从他们的实验中,你能得
到“一正一反”的概率是多少吗?
⑶对概率的研究而言小聪与小颖两位同学的实验说明了什么?
题号:4763514
题型:解答题
难易度:一般
日期:2017-07-29
来源:九年级数学(浙教版)上册同步练习:2.3 用频率估计概率
【题文】小强与小刚两位同学在学习“概率”时,做抛骰子(均匀立方体形状)试验,他们共抛了54次,出现不同向上点数的次数如下表:
(1)请计算出现向上点数为3的频率及出现向上点数为5的频率.
(2)小强说:“根据试验,一次试验中出现向上点数为5的概率最大.”小刚说:“如果抛540次,那么出现向上点数为6的次数正好是100次.”请判断小强和小刚说法的对错.
(3)如果小强与小刚各抛一枚骰子,求出现向上点数之和为3的倍数的概率.
题号:4763517
题型:解答题
难易度:一般
日期:2017-07-29
来源:九年级数学(浙教版)上册同步练习:2.3 用频率估计概率
【题文】某位篮球运动员在同样的条件下进行投篮练习,结果如下表:
投篮次数n
| 8
| 10
| 15
| 20
| 30
| 40
| 50
|
进球次数m
| 6
| 8
| 12
| 17
| 25
| 32
| 40
|
进球频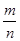
|
|
|
|
|
|
|
|
(1)计算并填写进球频率.
(2)这位运动员投篮一次,进球的概率约是多少(精确到0.1)?
(3)这位运动员投篮十次,必定会投进八球吗?为什么?
题号:4763536
题型:解答题
难易度:一般
日期:2017-07-29
来源:九年级数学(浙教版)上册同步练习:2.3 用频率估计概率
【题文】某地区林业局要考察一种树苗移植的成活率,对该地区这种树苗移植成活情况进行调查统计,并绘制了如图所示的统计表,根据统计图提供的信息解决下列问题:
⑴这种树苗成活的频率稳定在_________,成活的概率估计值为_______________.
⑵该地区已经移植这种树苗5万棵.
①估计这种树苗成活___________万棵;
②如果该地区计划成活18万棵这种树苗,那么还需移植这种树苗约多少万棵?

 .若再往盒中放进12颗同样的白色弹珠,取得白色弹珠的概率是
.若再往盒中放进12颗同样的白色弹珠,取得白色弹珠的概率是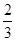 ,则原来盒中有白色弹珠__颗.
,则原来盒中有白色弹珠__颗.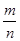

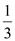 ;小颖反驳道:这里的“一正一反”实际上含有“一正一反,一反一正”二种情况,所以P(一正一反)=
;小颖反驳道:这里的“一正一反”实际上含有“一正一反,一反一正”二种情况,所以P(一正一反)=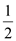 .
.