适用年级:{{getGradeNameByProperty('初三|同步测试|浙江|2017年')}} 试卷类型:{{getTestPaperTypeName('初三|同步测试|浙江|2017年')}} 使用省份:{{getAreaName('初三|同步测试|浙江|2017年')}}
试卷年份:{{getYear('初三|同步测试|浙江|2017年')}}上传日期:2017-07-27题数:11
提示:单击题文可显示答案与解析。
题号:3902209
题型:单选题
难易度:容易
日期:2017-07-27
来源:九年级数学(浙教版)上册同步练习:1.4 二次函数的应用(二)
【题文】某商家销售某种商品,当单价为10元时,每天能卖出200个.现在采用提高售价的方法来增加利润,已知商品单价每上涨1元,每天的销售量就少10个,则每天的销售金额最大为( )
| A.2500元 | B.2250元 |
| C.2160元 | D.2000元 |
题号:3902210
题型:单选题
难易度:一般
日期:2017-07-27
来源:九年级数学(浙教版)上册同步练习:1.4 二次函数的应用(二)
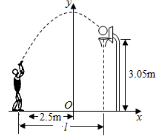
【题文】小伟在某次投篮中,球的运动路线是抛物线
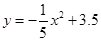
的一部分(如图),若命中篮圈中心,则他与篮底的距离
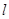
是()
题号:592432
题型:填空题
难易度:一般
日期:2015-07-30
来源:九年级数学(浙教版)上册同步练习:1.4 二次函数的应用(二)
【题文】某服装店购进单价为15元童装若干件,销售一段时间后发现:当销售价为25元时平均每天能售出8件,而当销售价每降低2元,平均每天能多售出4件.当每件的定价为________元时,该服装店平均每天的销售利润最大.
题号:3793220
题型:填空题
难易度:一般
日期:2017-06-17
来源:九年级数学(浙教版)上册同步练习:1.4 二次函数的应用(二)
【题文】某电商销售一款夏季时装,进价40元/件,售价110元/件,每天销售20件,每销售一件需缴纳电商平台推广费用a元(a>0)。未来30天,这款时装将开展“每天降价1元”的夏令促销活动,即从第1天起每天的单价均比前一天降1元。通过市场调研发现,该时装单价每降1元,每天销量增加4件。在这30天内,要使每天缴纳电商平台推广费用后的利润随天数t(t为正整数)的增大而增大,a的取值范围应为_____________。
题号:3902202
题型:填空题
难易度:一般
日期:2017-07-27
来源:九年级数学(浙教版)上册同步练习:1.4 二次函数的应用(二)
【题文】(3分)一个足球被从地面向上踢出,它距地面的高度h(m)与足球被踢出后经过的时间t(s)之间具有函数关系
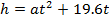
,已知足球被踢出后经过4s落地,则足球距地面的最大高度是
m.
题号:3902204
题型:填空题
难易度:容易
日期:2017-07-27
来源:九年级数学(浙教版)上册同步练习:1.4 二次函数的应用(二)
【题文】已知直角三角形的两直角边之和为2,则斜边长的最小值为___.
题号:3902207
题型:填空题
难易度:一般
日期:2017-07-27
来源:九年级数学(浙教版)上册同步练习:1.4 二次函数的应用(二)
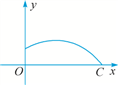
【题文】教练对小明推铅球的录像进行技术分析,发现铅球行进高度
y(
m)关于水平距离
x(
m)的函数表达式为
y=-

(
x-4)
2+3(如图所示),由此可知铅球推出的距离是_____
m.
题号:3898605
题型:解答题
难易度:一般
日期:2017-07-27
来源:九年级数学(浙教版)上册同步练习:1.4 二次函数的应用(二)
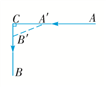
【题文】甲船和乙船分别从
A港和
C港同时出发,各沿图中箭头所指的方向航行(如图所示).现已知甲、乙两船的速度分别是16海里/时和12海里/时,且
A,
C两港之间的距离为10海里.问:经过多长时间,甲船和乙船之间的距离最短?最短距离为多少?(注:题中的“距离”都是指直线距离,图中
AC⊥
CB.)
题号:3902200
题型:解答题
难易度:一般
日期:2017-07-27
来源:九年级数学(浙教版)上册同步练习:1.4 二次函数的应用(二)
【题文】某商贸公司购进某种水果的成本为20元/千克,经过市场调研发现,这种水果在未来48天的售价
p(元/千克)与时间
t(天)之间的函数表达式为
p=
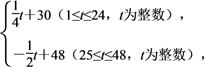
且其日销售量
y(kg)与时间
t(天)的关系如下表:
时间t(天)
| 1
| 3
| 6
| 10
| 20
| 40
| …
|
日销售量y(kg)
| 118
| 114
| 108
| 100
| 80
| 40
| …
|
(1)已知
y与
t之间的变化规律符合一次函数关系,试求第30天的日销售量是多少?
(2)问:哪一天的销售利润最大?最大日销售利润为多少?
(3)在实际销售的前24天中,公司决定每销售1 kg水果就捐赠
n元利润(
n<9)给“精准扶贫”对象.现发现:在前24天中,每天扣除捐赠后的日销售利润随时间
t的增大而增大,求
n的取值范围.
题号:3902201
题型:解答题
难易度:较难
日期:2017-07-27
来源:九年级数学(浙教版)上册同步练习:1.4 二次函数的应用(二)
【题文】如图,排球运动员站在点O处练习发球,将球从O点正上方2m的A处发出,把球看成点,其运行的高度y(m)与运行的水平距离x(m)满足关系式y=a(x﹣6)
2+h.已知球网与O点的水平距离为9m,高度为2.43m,球场的边界距O点的水平距离为18m.
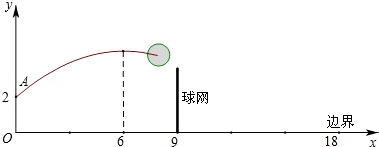
(1)当h=2.6时,求y与x的关系式(不要求写出自变量x的取值范围)
(2)当h=2.6时,球能否越过球网?球会不会出界?请说明理由;
(3)若球一定能越过球网,又不出边界,求h的取值范围.
题号:3902206
题型:解答题
难易度:容易
日期:2017-07-27
来源:九年级数学(浙教版)上册同步练习:1.4 二次函数的应用(二)
【题文】向上抛掷一个小球,小球在运行过程中,离地面的距离为
y(
m),运行时间为
x(s),
y与
x之间存在的关系为
y=-
 x2
x2+3
x+2.问:小球能达到的最大高度是多少?
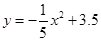 的一部分(如图),若命中篮圈中心,则他与篮底的距离
的一部分(如图),若命中篮圈中心,则他与篮底的距离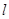 是()
是()
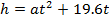 ,已知足球被踢出后经过4s落地,则足球距地面的最大高度是 m.
,已知足球被踢出后经过4s落地,则足球距地面的最大高度是 m. (x-4)2+3(如图所示),由此可知铅球推出的距离是_____m.
(x-4)2+3(如图所示),由此可知铅球推出的距离是_____m.

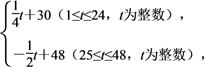

 x2+3x+2.问:小球能达到的最大高度是多少?
x2+3x+2.问:小球能达到的最大高度是多少?